快速区分清楚图形渲染中的AABB,KD树和BVH这些概念
主要想形象去区分好这些术语,目的是扫盲,先开好坑,内容持续填充。
0.先摆出这些词的全称
- AABB: 原名:axis aligned bounding box;中文直译名:轴对齐包围盒。一般常见也会叫它aabb盒。
- KD Tree: 原名:K-dimension tree, dimension是维度的意思。中文直译:KD树。
- BVH: 原名Bounding Volume Hierarchies,Hierarchies是层次、结构的意思;中文直译名:层次包围盒。常见也会叫它BVH树(搞得人家对BVH是树还是盒傻傻分不清)
强烈建议无视中文直译名,因为无法帮助理解还看得人糊里糊涂,想记住理解这几个名词,最好以图为准,脑海中知道它们长什么样的(正如你对链表、二叉树这个数据结构的印象一样去理解)。
1.AABB(axis aligned bounding box)
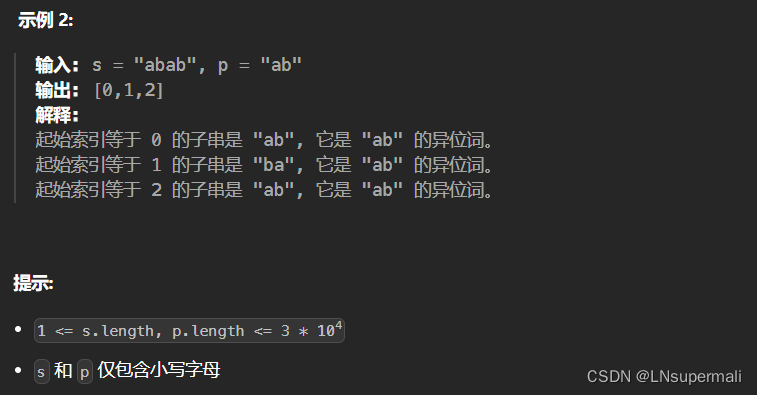
AABB长的是白色线框这样,包围住兔子,兔子完全在AABB内:

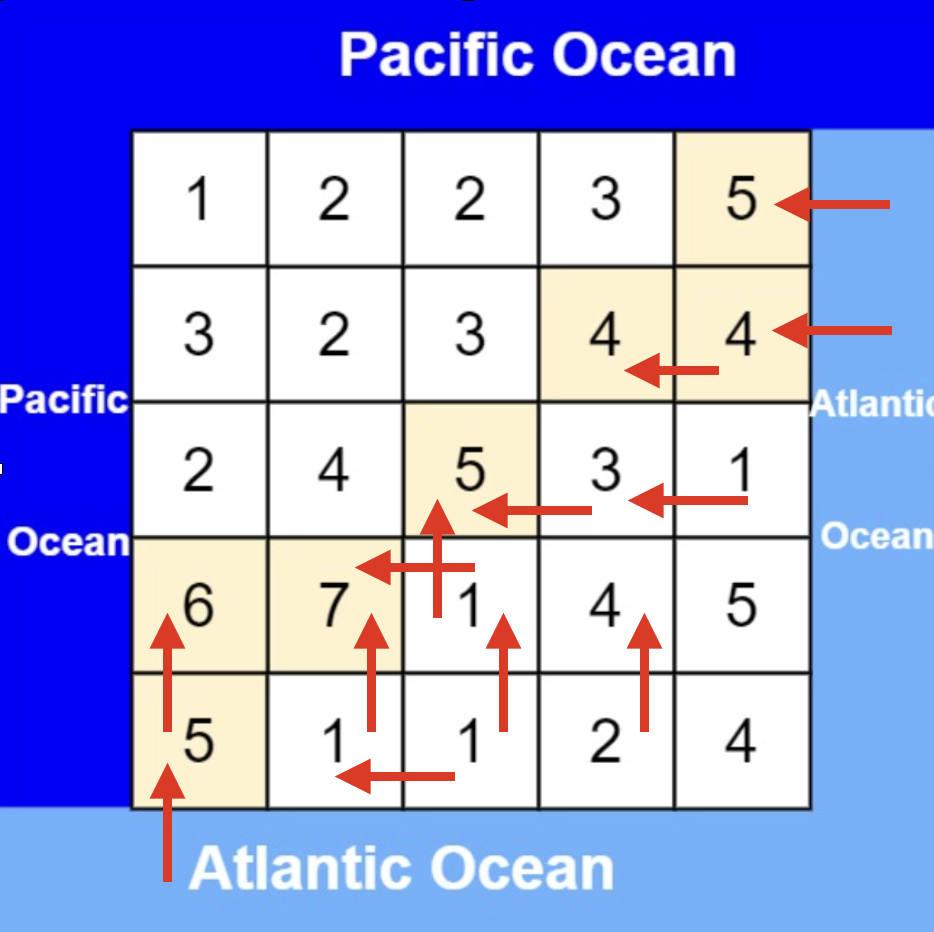
你的一个三维模型,读入三维场景中,便坐落在了世界坐标系上(图中红绿蓝轴线分布对应xyz轴线),你的模型实际上是网格模型,许多个三维顶点组成模型的表面,那每个三维顶点都可以被xyz表示。
那么最简单最快速地去评估这个模型在场景中占了多少空间,就是去看模型分布在X、Y和Z轴的最小值和最大值是多少,只需要遍历每个顶点坐标,找出X、Y和Z的最小值和最大值。一共六个值,可以组成一个最小值点和一个最大值点。而X、Y和Z的最小值和最大值所包括的空间范围就是AABB,如上图的白色线框。(顺便一提:那最小值点和最大值点其实刚好是在对角。)
AABB是个立方体,是个盒子,里面包着就是模型,那是不是需要写一个类,或者写个数据结构去记录维护这个AABB呢?——其实不需要,因为我要的是最简单最快速,所以记录好六个值就能记录好AABB了(当然是不需要像上图那样可视化的情况下,只需要一个数组把X、Y和Z的最小值和最大值存储起来即可)。
所以AABB通常作为一个类属性放进模型数据这个类里面。
说一个AABB最直观的好处,假如一个兔子模型有几万个三角形组成,我现在做光线追踪渲染,我要判断一条光线有没有照射到兔子模型,那我先跟兔子的AABB(只有六个值)做相交检测,可以很快速地发现没有相交,那么就可以直接跳过兔子模型,几万个三角形都可以无视掉了,是不是很牛逼!
所以AABB很简单,但是在很多应用方面的第一步就已经能提供很大的帮助。
AABB与KD Tree和BVH的关系
我把AABB跟KD Tree和BVH放到一起,难道BVH这种词是指斜着放或者最小包围住模型的多边盒子吗?
其实AABB跟KD Tree和BVH根本不是一个维度的东西,但是我在接触图形渲染初期,就经常会想搞清楚AABB和BVH的区别,因为看中文直译名两个都说是盒子,一个轴对齐包围盒,一个层次包围盒,我就以为是类似的东西(像B树和B+树那样)要做区别,所以我才会强烈建议无视中文直译名。
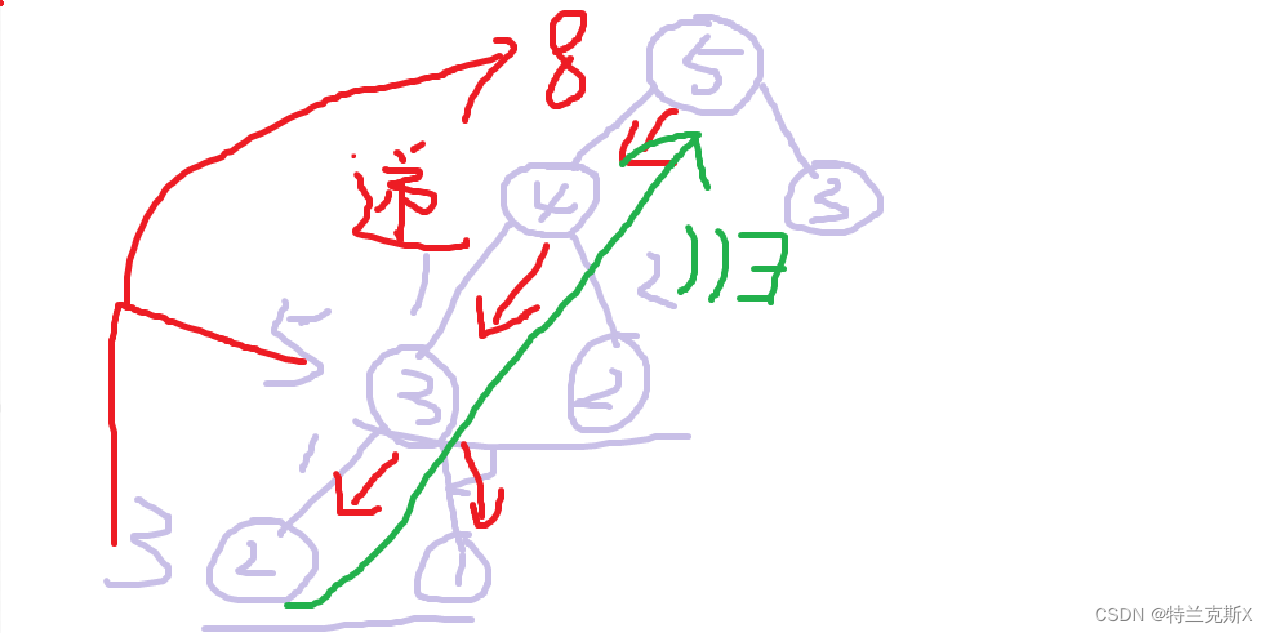
先简单去说清楚,KD Tree和BVH是两种对空间做划分组织的方法,也可以说是数据结构,但是本质上还是对空间划分组织方式的不同。它们都会用到AABB,这就是它们之间的联系,KD Tree和BVH是方法,需要用到模型中AABB这个属性。
为什么需要KD Tree或者BVH对空间去做划分组织?
我们继续刚刚AABB中光线寻找照射点的例子,光线没有与兔子的AABB相交倒好,可以直接无视跳过几万个三角形不用管啦。但是万一光线与AABB相交了呢,那不得继续往几万个三角形里面钻啊,那这时光线要逐一与兔子表面的每个三角形做相交才能知道光线照射到哪一个三角形,如果光线找了前几个三角形就发现相交了还好说,万一要找到最后一个三角形才能发现相交,这个计算量想想都可怕(相交计算正是光线追踪渲染中消耗时间的大头)
最直观的解决想法:
那我们就会去想方法减少无用功,例如我们想着能不能先判断光线与AABB的左半部分相交还是右半部分相交呢,然后不就可以排除掉将近一半的三角形了嘛,假如光线跟AABB的左半部分相交,那不是可以继续对该部分分下左右再去判断和排除了,一步步递进到最后才到三角形,不要一来就跟最小的三角形判断相交嘛。整个过程不就省下很多计算了吗
刚刚好这个想法就形成了KD Tree的雏形,或者说KD Tree就是这么想的,就是如此去对空间做划分,另外还有在上面想法中没有想到的组织方式的问题。
2.KD Tree(K-dimension tree)
其实记住简称和英文全称都对理解没多大帮助,看英文直译就是k维度树,完全不知道啥玩意,所以还是记形象的图片吧。
我们图形渲染都是跟三维空间打交道,网上很多解释都是拿二维图来说事,很难转过来验身都三维空间去理解,所以去理解KD Tree,应该直接用三维的方式去理解。
三维指的是x,y和z三个维度,KD Tree你往宏观去说,可以很多个维度,但是我们就在图形渲染中用,我们就看在图形渲染中怎么用的,用的就是三维的,我们就看x,y和z三个维度,其他的不管(但是原理是同样的,像多幂次的展开实际就是多次乘法一样)。
我们看看图片吧
3.BVH(axis aligned bounding box)
BVH的目的跟KD Tree是一样的——都是为了将模型中的三角形组织地更高效——》使得在找三角形的时候更高效省时。