数据结构、算法总述:数据结构/算法 C/C++-CSDN博客
二分图:节点由两个集合组成,且两个集合内部没有边的图。换言之,存在一种方案,将节点划分成满足以上性质的两个集合。
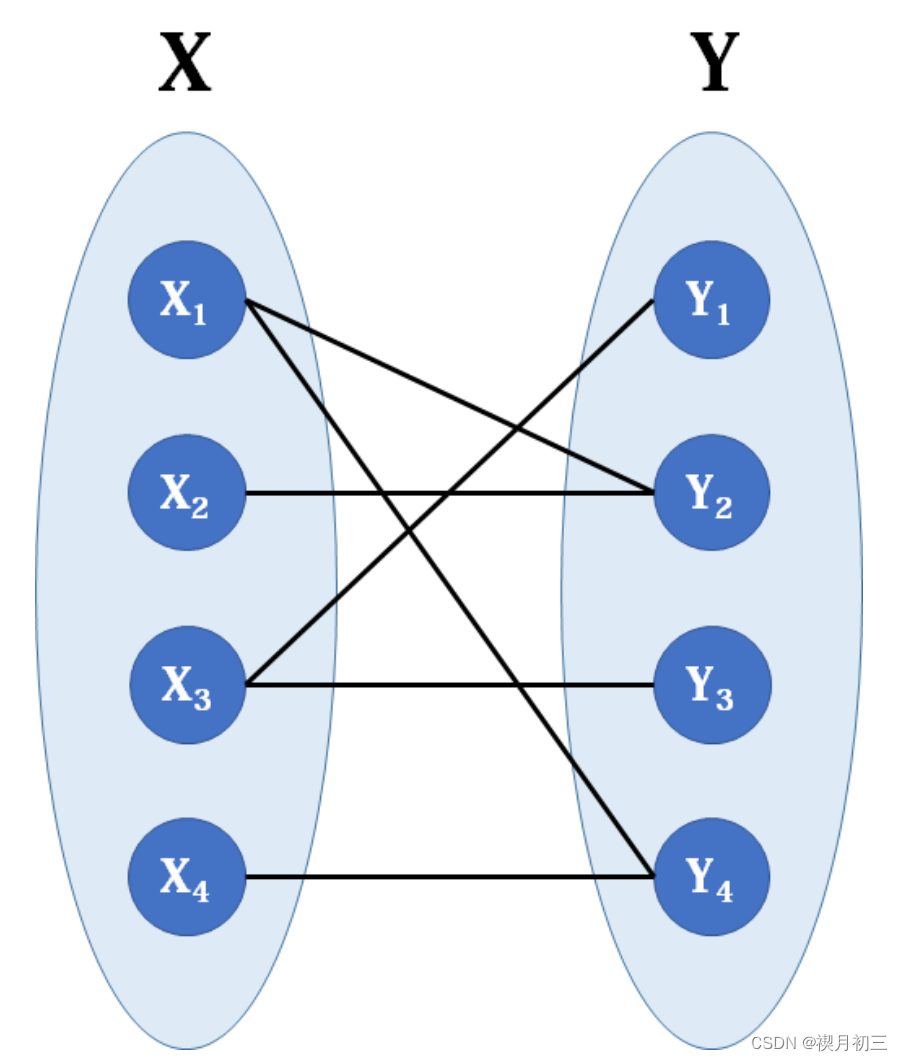
染色法
目的:验证给定的二分图是否可以进行二色染色
时间复杂度是
O(n+m)
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色,-1表示未染色,0表示白色,1表示黑色
// 参数:u表示当前节点,c表示当前点的颜色
bool dfs(int u, int c)
{
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (color[j] == -1)
{
if (!dfs(j, !c)) return false;
}
else if (color[j] == c) return false;
}
return true;
}
bool check()
{
memset(color, -1, sizeof color);
bool flag = true;
for (int i = 1; i <= n; i ++ )
if (color[i] == -1)
if (!dfs(i, 0))
{
flag = false;
break;
}
return flag;
}题目:
860. 染色法判定二分图 - AcWing题库![]() https://www.acwing.com/problem/content/862/
https://www.acwing.com/problem/content/862/
匈牙利算法
我们可以看做一个月老在牵红线,现在左边是男生,右边是女生,互相都有心仪的对象,我们就要尽量每一个男生都好。然后就出现了一个图。
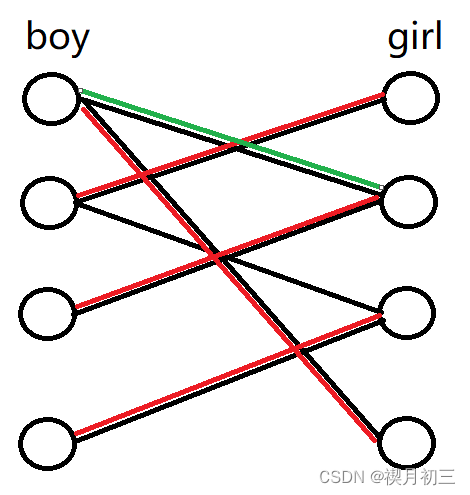
我们先看第一个男生,他有两个心仪的对象,先看第一个女生,还是单身,那就选第一个,然后看下一位,也是第一个单身,就她了。但是第三位男生就出问题了,他只有一位心仪的对象,但是呢,那位已经有对象了,但是这位男生还是不放弃,找到那个男朋友,说:“要不你换一换”。我们再一看,确实还有一个备胎单身,就换一个,这样两个人都好,最后一个也很正常,直接匹配。所以总结出十六字真言:待字闺中,据为己有;名花有主,求他放手。 所以说这也告诉我们不要轻易放弃,最后悔的不是做错,而是错过。
时间复杂度
O(n*m),实际运形时间远小于n*m
int n1, n2; // n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx; // 邻接表存储所有边,匈牙利算法中只会用到从第一个集合指向第二个集合的边,所以这里只用存一个方向的边
int match[N]; // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N]; // 表示第二个集合中的每个点是否已经被遍历过
bool find(int x)
{
for (int i = h[x]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true;
if (match[j] == 0 || find(match[j]))
{
match[j] = x;
return true;
}
}
}
return false;
}
// 求最大匹配数,依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
memset(st, false, sizeof st);
if (find(i)) res ++ ;
}题目:
861. 二分图的最大匹配 - AcWing题库![]() https://www.acwing.com/problem/content/863/
https://www.acwing.com/problem/content/863/








![ElasticSearch文档批量操作[ES系列] - 第503篇](https://img-blog.csdnimg.cn/img_convert/4872bc1ecd01a0d1df4022cb7a9ef9ac.png)