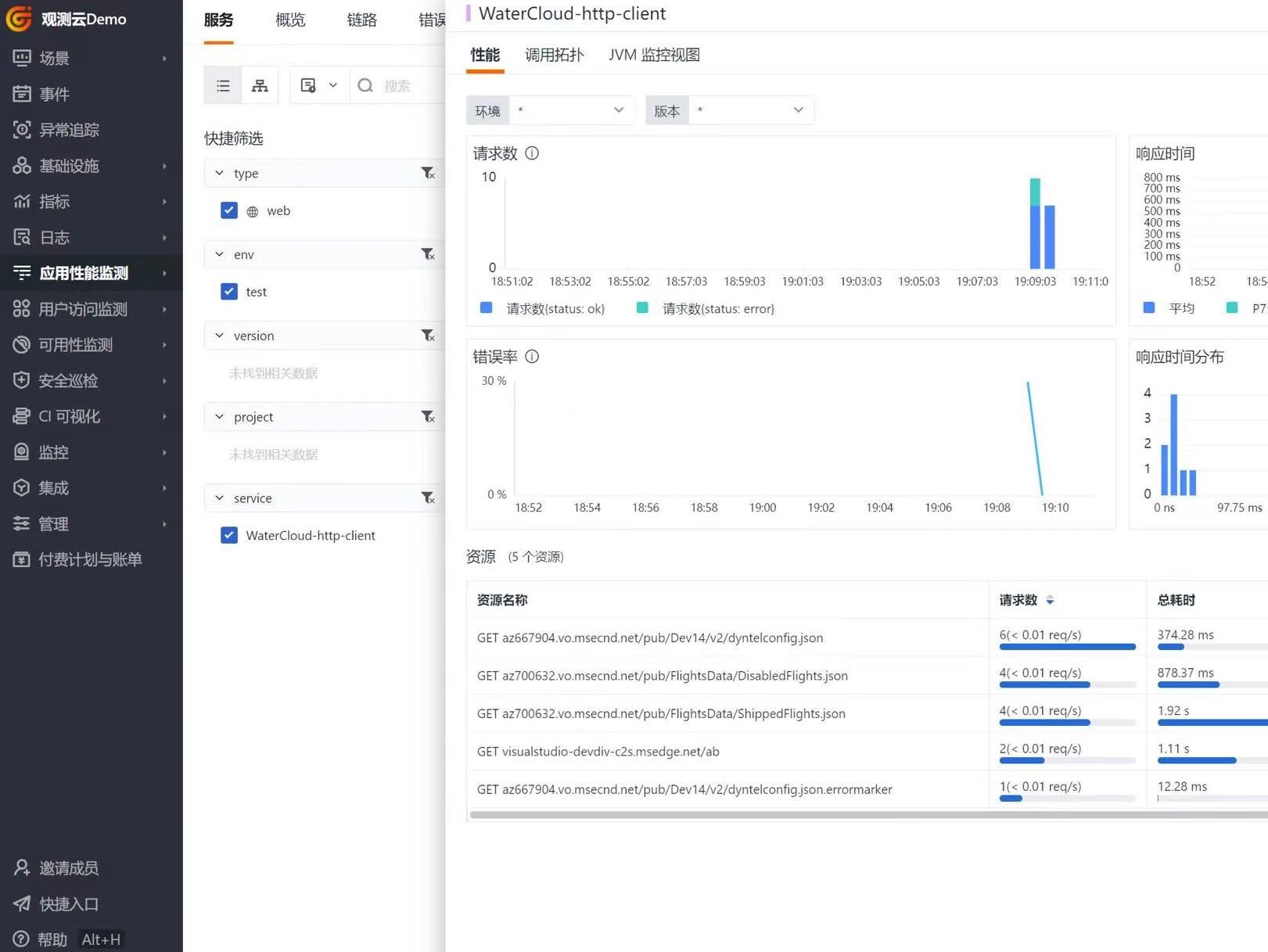
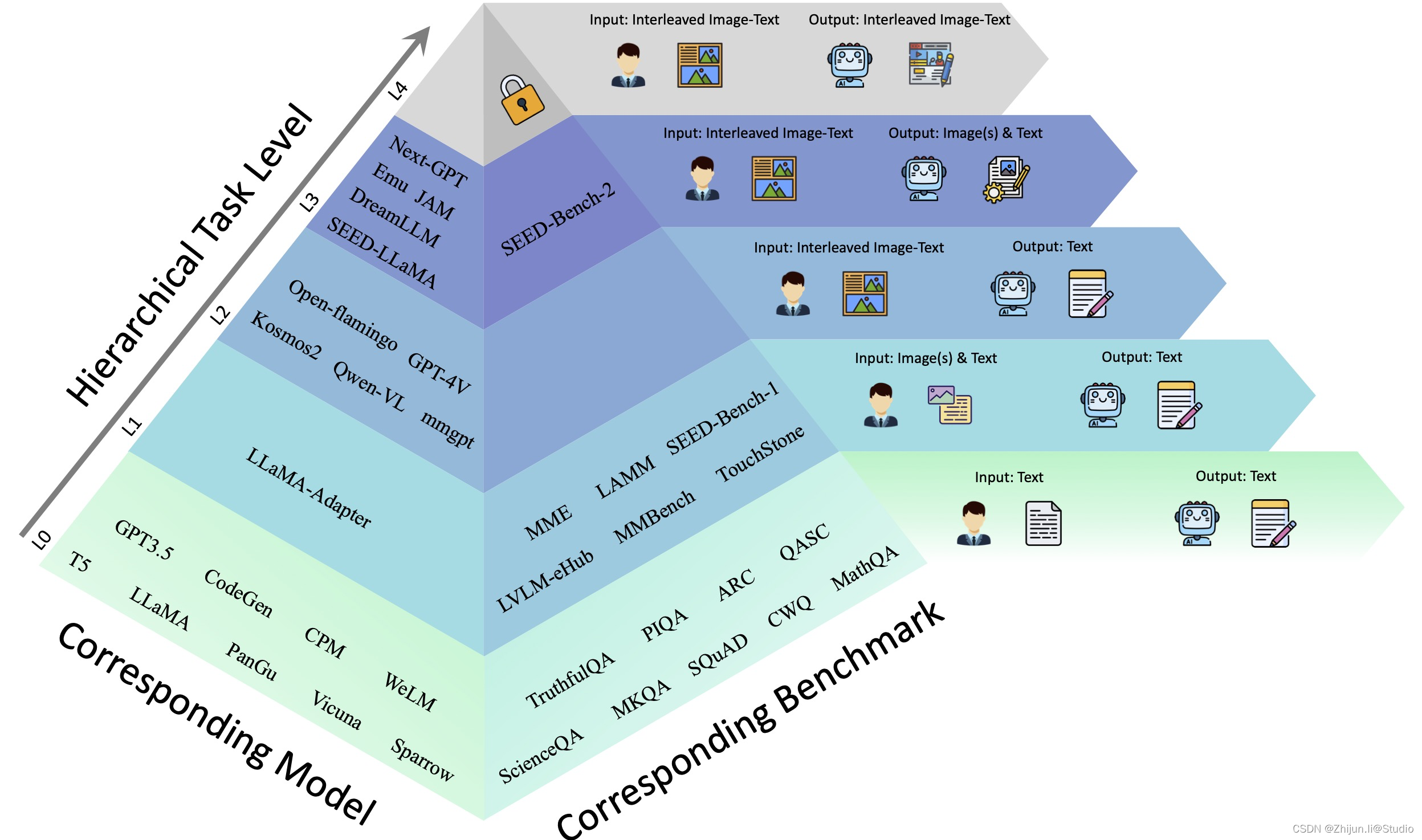
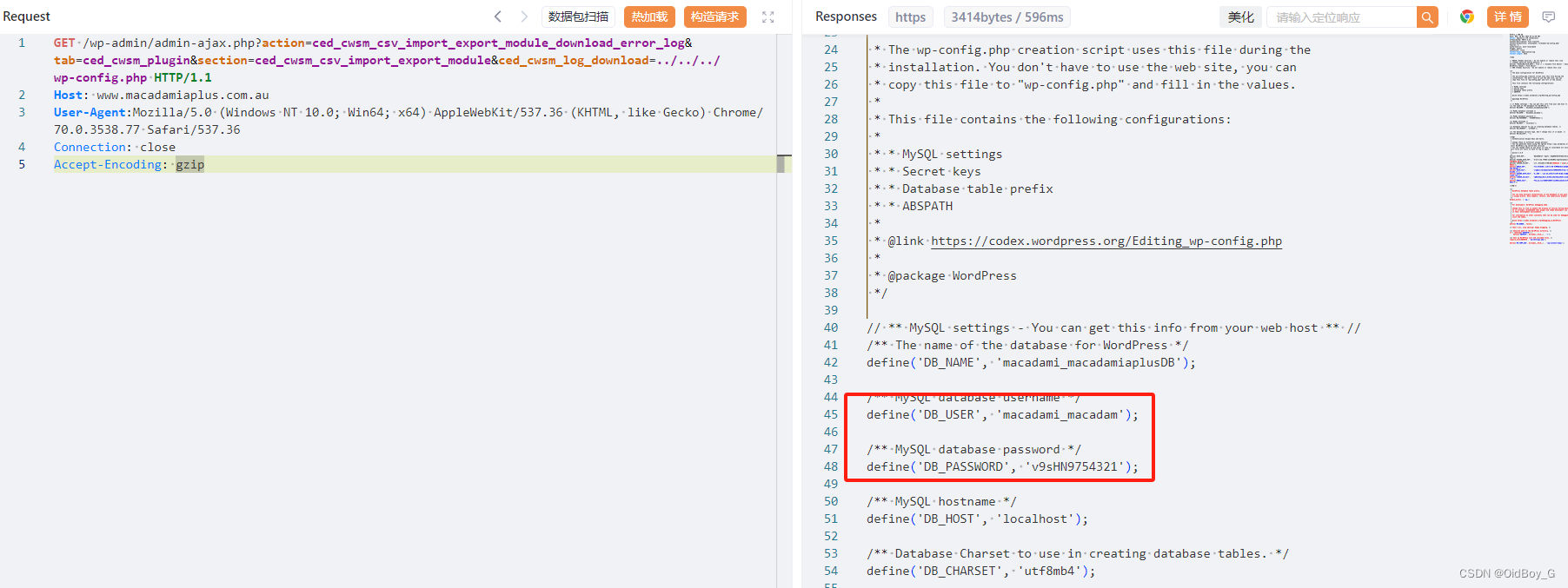
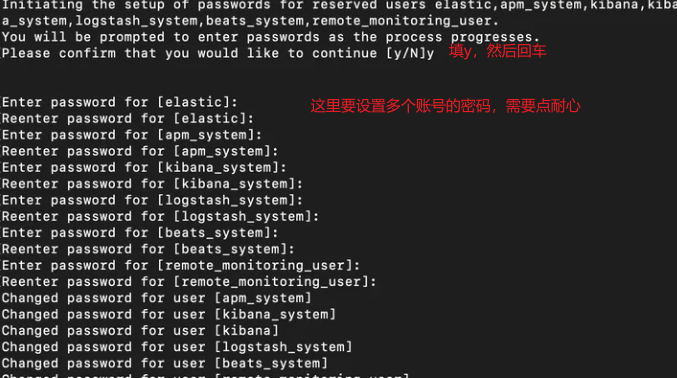
文章目录
- 406. 根据身高重建队列
- 题目描述
- 贪心算法
- 代码
406. 根据身高重建队列
题目描述
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
示例 2:
输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
提示:
- 1 <= people.length <= 2000
- 0 <= hi <= 106
- 0 <= ki < people.length
- 题目数据确保队列可以被重建
贪心算法
本题有两个维度,h和k,看到这种题目一定要想如何确定一个维度,然后再按照另一个维度重新排列。
其实如果大家认真做了135. 分发糖果,就会发现和此题有点点的像。
在135. 分发糖果我就强调过一次,遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。
如果两个维度一起考虑一定会顾此失彼。
对于本题相信大家困惑的点是先确定k还是先确定h呢,也就是究竟先按h排序呢,还是先按照k排序呢?
如果按照k来从小到大排序,排完之后,会发现k的排列并不符合条件,身高也不符合条件,两个维度哪一个都没确定下来。
那么按照身高h来排序呢,身高一定是从大到小排(身高相同的话则k小的站前面),让高个子在前面。
此时我们可以确定一个维度了,就是身高,前面的节点一定都比本节点高!
那么只需要按照k为下标重新插入队列就可以了,为什么呢?
以图中{5,2} 为例:

按照身高排序之后,优先按身高高的people的k来插入,后序插入节点也不会影响前面已经插入的节点,最终按照k的规则完成了队列。
所以在按照身高从大到小排序后:
局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性
全局最优:最后都做完插入操作,整个队列满足题目队列属性
局部最优可推出全局最优,找不出反例,那就试试贪心。
整个插入过程如下:
排序完的people: [[7,0], [7,1], [6,1], [5,0], [5,2],[4,4]]
插入的过程:
插入[7,0]:[[7,0]]
插入[7,1]:[[7,0],[7,1]]
插入[6,1]:[[7,0],[6,1],[7,1]]
插入[5,0]:[[5,0],[7,0],[6,1],[7,1]]
插入[5,2]:[[5,0],[7,0],[5,2],[6,1],[7,1]]
插入[4,4]:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
此时就按照题目的要求完成了重新排列。
代码
这段代码实现了一个有趣的问题:根据人群的身高和每个人前面身高不低于该人的人数来重建队列。这是一个贪心算法的应用,其中处理的核心思想是先安排身高较高的人,然后再依次安排身高较低的人,利用了排序和列表插入的技巧。下面是对这段代码的详细注释:
class Solution {
public:
// 自定义比较函数,用于排序
static bool cmp(vector<int>& a,vector<int>& b)
{
// 如果身高相等,则按照 k 值(即队列中前面不低于自己身高的人数)升序排序
// 这样可以保证相同身高的人按照他们的 k 值正确排序
if(a[0]==b[0]) return a[1]<b[1];
// 否则,按照身高降序排序
return a[0]>b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
vector<vector<int>> que; // 初始化空队列
// 对 people 数组进行排序,排序规则由自定义的 cmp 函数决定
sort(people.begin(),people.end(),cmp);
// 遍历排序后的人群
for(int i=0;i<people.size();i++)
{
int pos=people[i][1]; // 获取当前人前面应有的不低于自己身高的人数,即 k 值
// 在队列的指定位置插入当前人的信息
// pos 位置正好保证了该人前面有 pos 个不低于自己的身高的人
que.insert(que.begin()+pos,people[i]);
}
// 返回重构后的队列
return que;
}
};
代码的逻辑如下:
- 首先,通过自定义排序规则(先按身高降序排序,身高相同则按 k 值升序排序),对输入的 people 数组进行排序。这样做的目的是确保在遍历并插入每个人到队列时,队列中已存在的人都是身高不低于当前人的,从而满足题目中的 k 值的要求。
- 然后,遍历排序后的数组,对于每个人,根据他们的 k 值,也就是他们前面应有的不低于自己身高的人数,在队列的相应位置插入他们的信息。由于是降序排序,此时插入位置之前的人都是身高不低于当前人的,因此这一步可以确保每个人的 k 值要求得到满足。
- 最后,返回重构后的队列。
这种方法巧妙地利用了排序和列表插入操作,有效地解决了问题,展示了贪心算法在实际问题中的应用。

![[flask]cookie的基本使用/](https://img-blog.csdnimg.cn/direct/53d9e47e4b91420187a59faa2ba89a8d.png)