1.常用的爬虫库
(1)在setting的project里面点击Python Interpreter
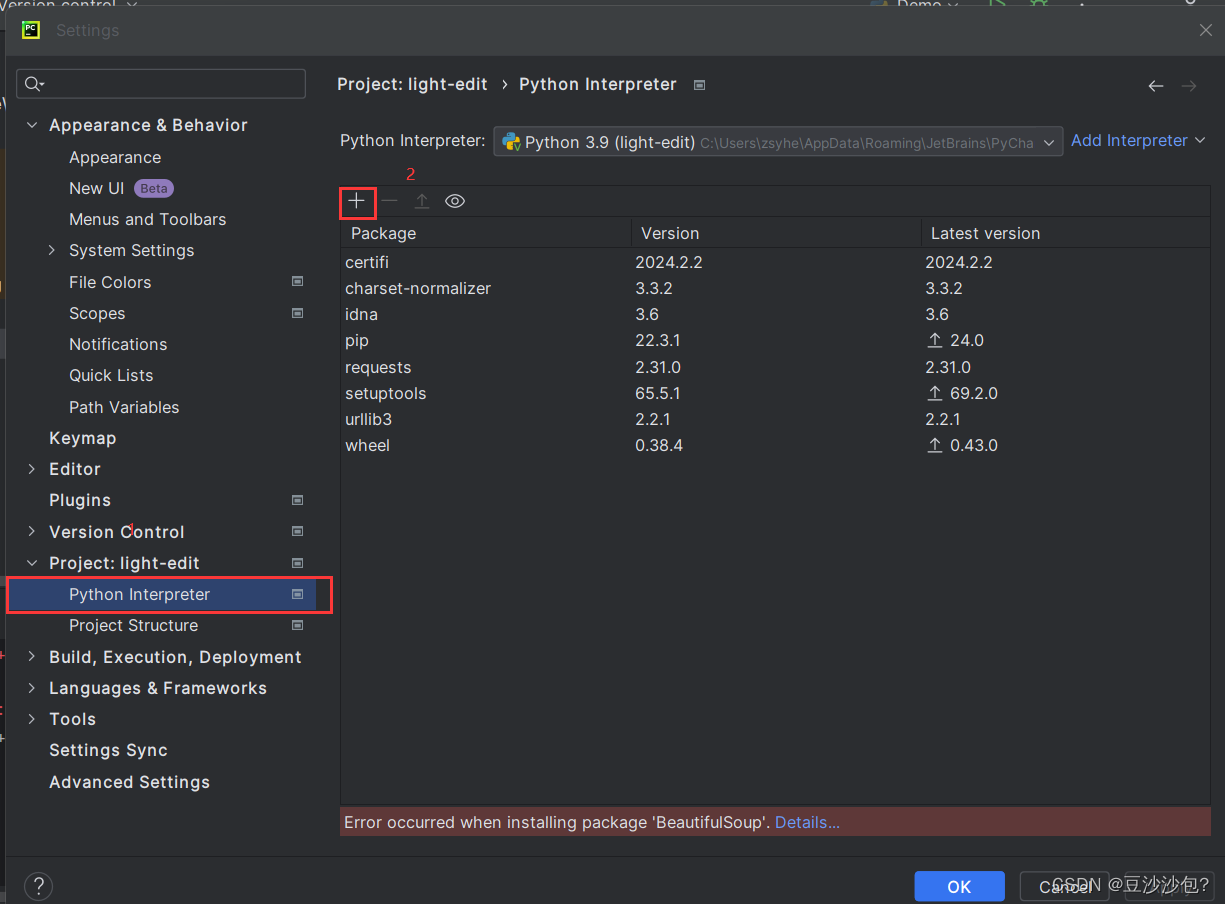
(2)常用的爬虫库有
import requests
//用途:用于发送HTTP请求。
from bs4 import BeautifulSoup
//用于从HTML或XML文档中提取数据。
import scrapy
//一个功能强大的爬虫框架,用于大规模的数据提取。
from selenium import webdriver
//用途:用于自动化浏览器操作,如JavaScript渲染页面的爬取。
from pyquery import PyQuery as pq
//用途:类似于jQuery的选择器,用于解析和操作HTML文档。
from lxml import etree
//于处理XML和HTML文档。
import tesserocr
//用于OCR(光学字符识别),从图像中提取文本。
import aiohttp
//异步HTTP客户端/服务器框架。
3.如果在setting里面下载不了,就直接切换到cmd窗口
任何目录下打开命令行窗口(例如Windows的命令提示符或Linux/macOS的终端),然后输入python -m pip install --upgrade pip命令。不需要特定的目录,只要您的Python环境已正确配置并且pip可用即可。
python -m pip install --upgrade pip
python -m pip install --index-url=https://pypi.org/simple/ pyquery
4.然后打开cmd窗口pip安装
pip install requests beautifulsoup4 scrapy selenium pyquery lxml tesserocr aiohttp