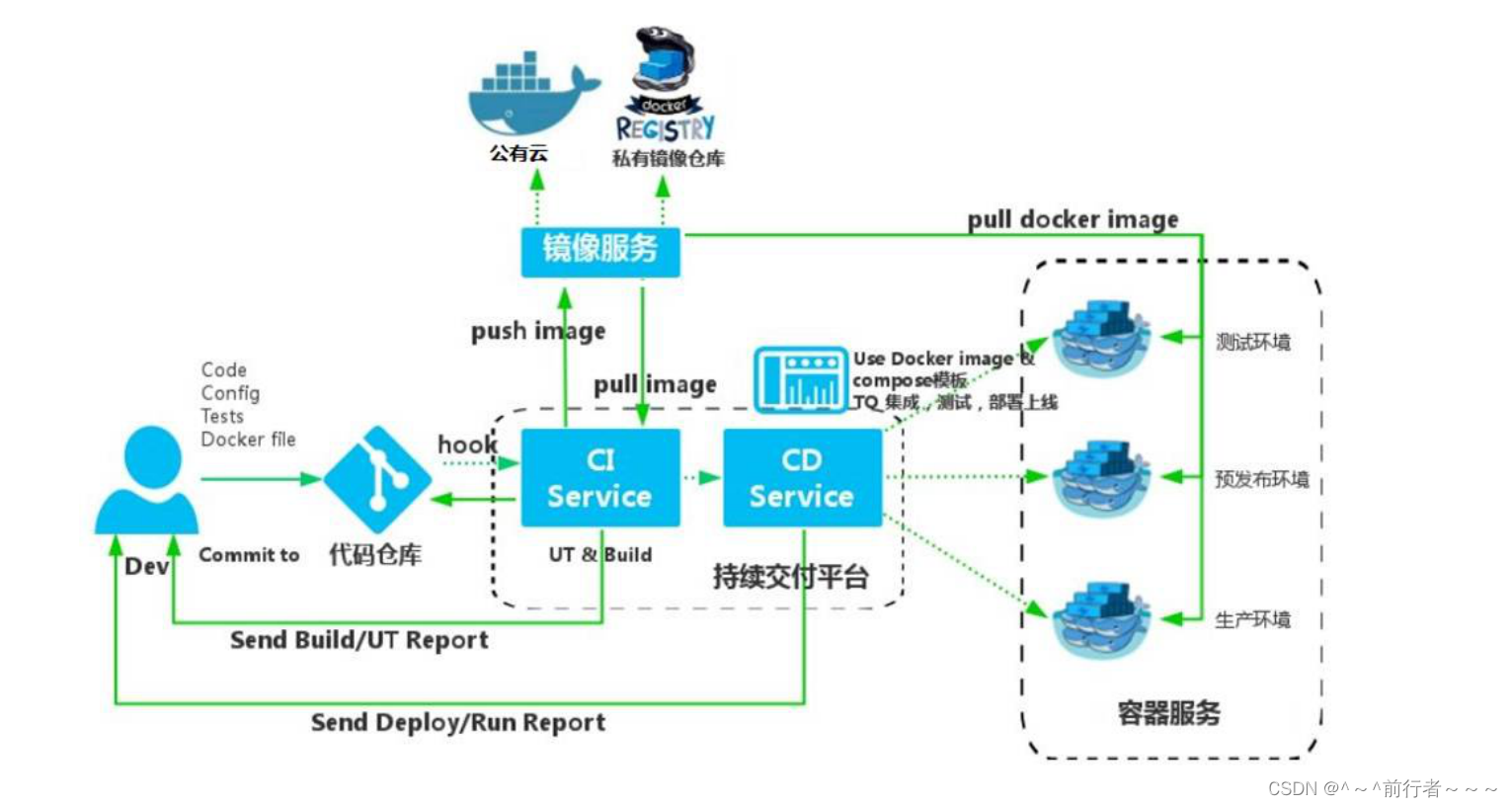
coco creator 3.x: 居中展示

news2024/9/23 19:58:48

coco creator 3.x 里面有很多需要居中处理，下面积累记录一些日常的实验。
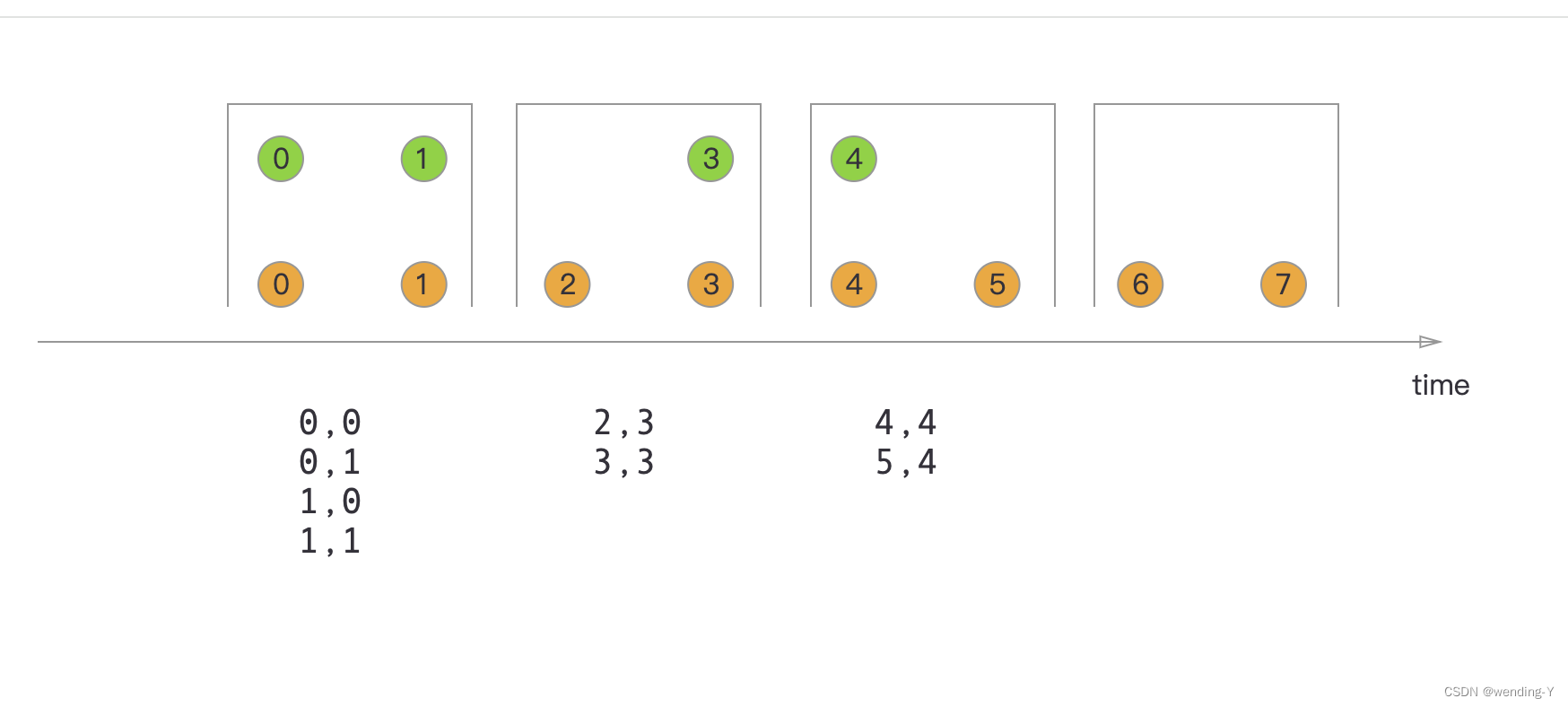
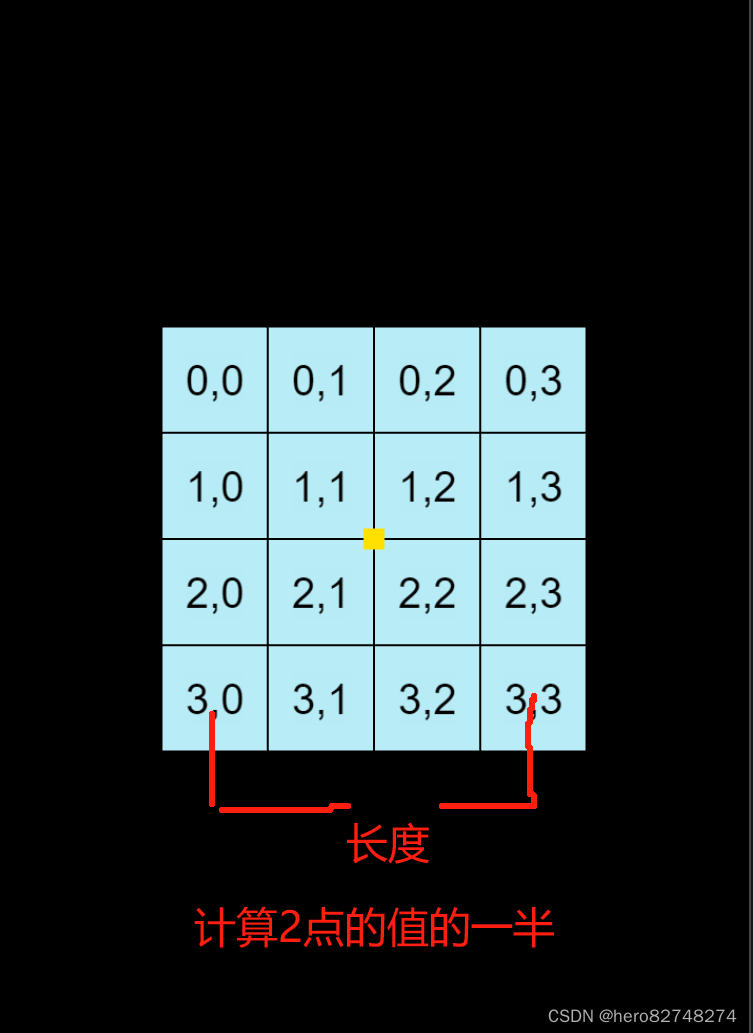
下面一张图如下，在这张图里面创建了一个3x3的展示。但是这个展示过程并不在居中展示。而它的容器节点恰恰就在中心点位置。所以在创建后，布局预制体元素并不能实现居中的视觉。那样，我们只需要将里面元素偏移一个值即可计算处理这样效果。
在这里插入图片描述

import { instantiate } from 'cc';
import { Label } from 'cc';
import { Vec3 } from 'cc';
import { Prefab } from 'cc';
import { _decorator, Component, Node } from 'cc';
const { ccclass, property } = _decorator;

@ccclass('PosTest')
export class PosTest extends Component {

   @property(Prefab)
   public perfab:Prefab

    start() {
        this.init();

    }

    private init(){
        
        for(var i = 0; i < 4; i++){
            for(var j = 0; j < 4; j++){
                var item = instantiate(this.perfab);
                item.position = new Vec3(j* 102, -i*102);
                item.getChildByName("nameTxt").getComponent(Label).string = i+","+j;
                item.parent = this.node;
            }
        }       
    }

    update(deltaTime: number) {
        
    }
}

实验过程：对每一个元数进行位置偏移。

第一步想到的是将每一个元素都移动一个相同的位置值计算出要移动多少才能居中。

要居中，只要算出两点之间距离，再除以一半就能得出要的结果。

假设一：下面图中方块宽高为 100x100 ，在没有间隙和偏移的情况 刚好总宽为4x100 = 400的值，按除以一半即可偏移到居中位置了。

但是由于方块的锚点在居中位置。所以真正的计算方块的距离不能以左下角的角度去算了。这个时候，只需要减去1个方块宽，即可计算出两点距离了。

假设二没有间隙的计算： 4x100 - 100 = (4 -1)*100 / 2 这个就是能算出在没有间隙的情况。

假设三带上间隙的计算，间隙为2 ： 4x100 - 100 + （4-1）*2 = （4-1）*100+ （4-1）2 = （4-1） 102 这个就是正式的距离了，再除以2 即可获得居中了。
在这里插入图片描述

import { instantiate } from 'cc';
import { Label } from 'cc';
import { Vec3 } from 'cc';
import { Prefab } from 'cc';
import { _decorator, Component, Node } from 'cc';
const { ccclass, property } = _decorator;

@ccclass('PosTest')
export class PosTest extends Component {

   @property(Prefab)
   public perfab:Prefab

    start() {
        this.init();

    }

    private init(){
        
        //居中位置  =（ |开始点pos - 结束点pos| + （长度-1）*间缝隙） / 2
        //(4-1) * 100 + (4-1) * 2 

        for(var i = 0; i < 4; i++){
            for(var j = 0; j < 4; j++){
                var item = instantiate(this.perfab); //瞄点在居中
                var offx = ((4-1) * 102)/2;
                var offy = ((4-1) * 102)/2;
                item.position = new Vec3(j* 102-offx, -i*102+offy);
                item.getChildByName("nameTxt").getComponent(Label).string = i+","+j;
                item.parent = this.node;
            }
        }       
    }

    update(deltaTime: number) {
        
    }
}

以上通过计算获取到了位置，有时候我们希望0 0点位置在下面，而其他点位置在上面。这个时候通过改变方向接口。

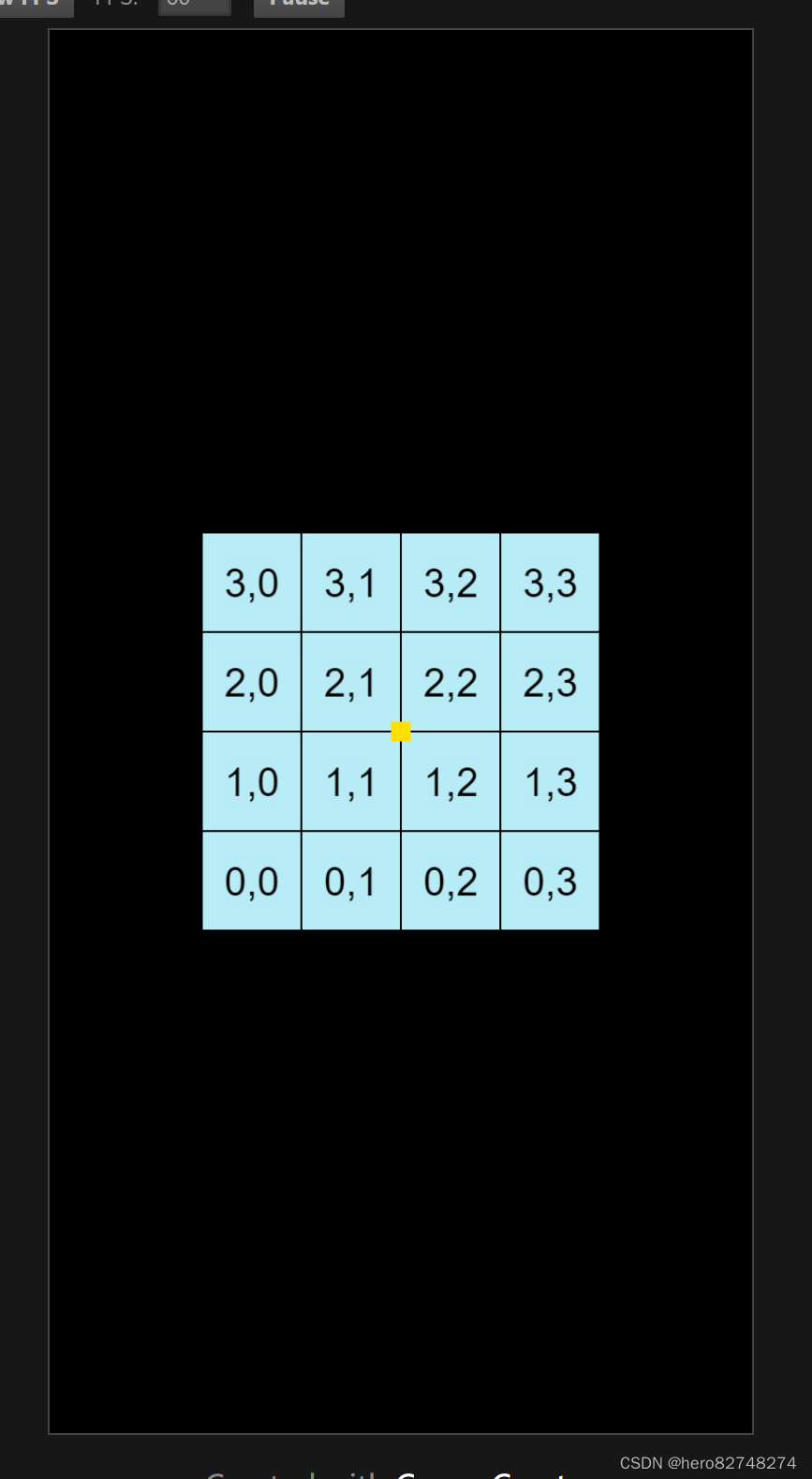
在这里插入图片描述
修改 item.position = new Vec3(j 102-offx, i*102-offy)*;这行代码让位置向下移动，则0，0位置就在底部了。

  for(var i = 0; i < 4; i++){
            for(var j = 0; j < 4; j++){
                var item = instantiate(this.perfab); //瞄点在居中
                var offx = ((4-1) * 102)/2;
                var offy = ((4-1) * 102)/2;
                item.position = new Vec3(j* 102-offx, i*102-offy);
                item.getChildByName("nameTxt").getComponent(Label).string = i+","+j;
                item.parent = this.node;
            }
        }