---

题目描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

示例 1:

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
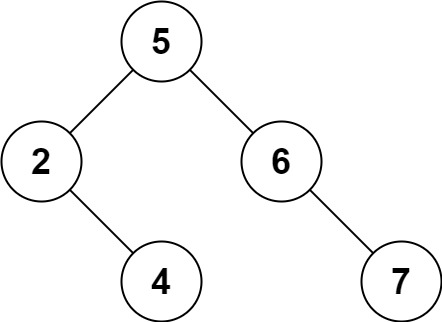
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:

输入: root = [], key = 0
输出: []

提示:

节点数的范围 [0, 104].
-105 <= Node.val <= 105
节点值唯一
root 是合法的二叉搜索树
-105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

思路

在代码中详细注释了

代码

class Solution {
    //使用递归的方法
    public TreeNode deleteNode(TreeNode root, int key) {
        //本方法采用的是：删除root的时候让左子树充当root，也就是示例一中的第二种答案
        //递归出口
        if (root==null){
            return null;
        }
        //如果找到了key，需要删除root这个节点，需要左右子树调整，所以选择采用后序遍历的方式，能够利用左右子树返回的结果
        TreeNode leftChild = deleteNode(root.left,key);//得到左子树的根节点
        TreeNode rightChild = deleteNode(root.right,key);//得到右子树的根节点
        //调整root的左右子树
        root.left = leftChild;
        root.right =rightChild;
        if (root.val==key){//找到key
            //如果这个节点是叶子节点就直接删除就行了，也就是直接返回null
            if (leftChild==null&&rightChild==null){
                return null;
            }
            //左子树为空就返回右子树
            if (leftChild==null){
                return rightChild;
            }
            //右子树为空就返回左子树
            if (rightChild==null){
                return leftChild;
            }else {
                //如果右子树不为空就对子树的结构做出调整
                TreeNode cur = rightChild;
                //找到右子树中最左下方的节点，因为需要让这个节点的左孩子指向leftChild的右孩子
                //可以拿[5,3,6,2,4,null,7] key=5 这个案例在纸上画一下，删除5之后，4需要挂在6的左孩子的地方才符合二叉搜索树
                while (cur.left!=null){
                    cur = cur.left;
                }
                cur.left = leftChild.right;
            }
            //删除根节点，左子树成为根节点
            leftChild.right = rightChild;
            return leftChild;
        }
        return root;
    }
}