今日任务:
1)110.平衡二叉树
2)257. 二叉树的所有路径
3)404.左叶子之和
110.平衡二叉树
题目链接:110. 平衡二叉树 - 力扣(LeetCode)
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1示例 1:
给定二叉树 [3,9,20,null,null,15,7]
输出:true示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
输出:False
文章讲解:代码随想录 (programmercarl.com)
视频讲解:后序遍历求高度,高度判断是否平衡 | LeetCode:110.平衡二叉树哔哩哔哩bilibili
思路:
node的高度:node节点到最底层叶子节点的高度
这题弄清楚这个就比较好做了,采用递归法后序遍历(左右中)
1.确定递归函数的参数和返回值:将节点传入递归函数中,返回这个节点的高度
2.终止条件:递归的过程中依然是遇到空节点了为终止,返回0,表示当前节点为根节点的树高度为0
3.单层递归逻辑:判断传入节点左右两个子树的高度差是否超过1
如果不超过1,说明是平衡的,则继续检查其左右子树是否也是平衡的。如果超过1,则不平衡,直接返回false。因为返回值为高度,这里为了返回值类型统一,我们可以将不平衡设为-1,如果返回值为-1,则表示不平衡;否则平衡,返回该节点高度
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def isBalanced(self, root: [TreeNode]) -> bool:
if self.getHeight(root) != -1:
return True
else:
return False
def getHeight(self, node):
if not node:
return 0
leftHeight = self.getHeight(node.left) # 左
rightHight = self.getHeight(node.right) # 右
if leftHeight == -1 or rightHight == -1:
return -1 # 这里直接终止返回-1,不要在用height记录了,因为左右高度均为-1时,在后面判断中,两个相减是等于0的,会使height重新赋值为0
else:
height = max(leftHeight, rightHight) + 1 # 求出该节点高度
# 如果左右子树高度差大于1,则用-1标记
if abs(leftHeight - rightHight) > 1:
height = -1
# 如果之前没有返回-1,则表明该节点之前的子树都符合要求
return height感想:
避免重复计算: 为了避免重复计算,这题我们采用下而上的方式计算节点,也就是后序遍历,这样可以确保每个节点的高度只计算一次
适时剪枝: 在检查节点平衡性时,如果发现某个节点所在的子树已经不平衡,可以及早终止递归,提前返回结果,避免不必要的计算。
257. 二叉树的所有路径
题目链接:257. 二叉树的所有路径 - 力扣(LeetCode)
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。示例:
输入:[1,2,3,None,5,None,None]
输出:["1->2->5","1->3"]
文章讲解:代码随想录 (programmercarl.com)
视频讲解:递归中带着回溯,你感受到了没?| LeetCode:257. 二叉树的所有路径哔哩哔哩bilibili
思路:
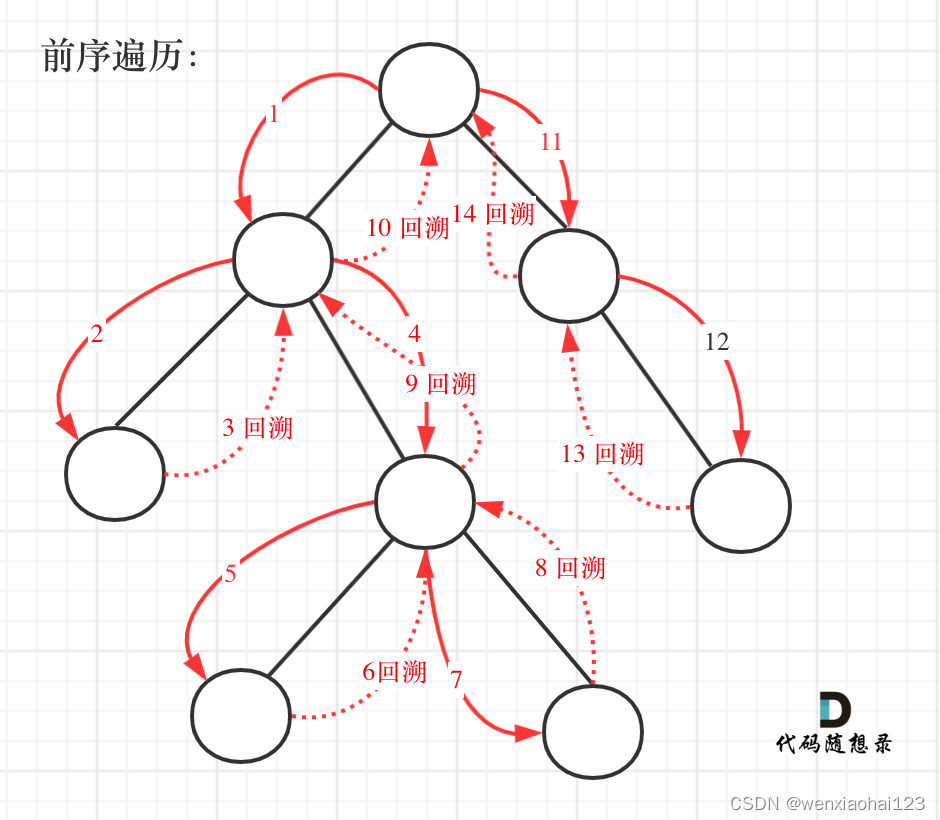
当我们想要找到二叉树中所有从根节点到叶子节点的路径时,可以使用深度优先搜索(DFS)算法(前序遍历-->中左右)。我们可以从根节点开始,沿着每条路径向下遍历二叉树,直到到达叶子节点。在遍历过程中,我们将经过的节点值记录下来,直到到达叶子节点,然后将路径添加到结果中。
下面是具体的实现逻辑:
1.创建一个空列表 result 用于存储所有的路径。
2.编写一个递归函数 traversal,它接收当前节点 node 和当前路径 path 作为参数。
3.在递归函数中,首先将当前节点的值加入到路径 path 中。
4.判断当前节点是否为叶子节点(即没有左右子节点)。如果是叶子节点,则将当前路径 path 加入到结果列表 result 中。
5.如果当前节点不是叶子节点,则递归调用 traversal 函数分别遍历其左右子节点。在递归调用时,需要将当前路径 path 作为参数传递给下一级。
6.最后,在主函数中调用 traversal 函数,从根节点开始遍历二叉树,并将结果返回。
思路比较简单,但要注意里面的回溯过程
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def binaryTreePaths(self, root: [TreeNode]) -> list[str]:
path = []
result = []
if not root:
return result
self.traversal(root, path, result)
return result
def traversal(self, node: [TreeNode], path: list[str], result: list[str]) -> None:
# 将当前节点值加入路径中
path.append(str(node.val)) # 中
# 遇到叶子节点终止
if not node.left and not node.right:
sPath = '->'.join(path)
result.append(sPath)
return
# 如果不是叶子节点,继续递归遍历左右子树
if node.left: # 左
self.traversal(node.left, path, result)
path.pop() # 回溯
if node.right: # 右
self.traversal(node.right, path, result)
path.pop() # 回溯这一种是比较完整的写法,后面采用了隐藏回溯的方法。隐藏回溯方法核心是为了保证path的独立性,我们需要构建新的字符串传入,而不是path本身
第一种采用列表切片实现,相当于传入的path副本
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution2:
def binaryTreePaths(self, root: [TreeNode]) -> list[str]:
path = []
result = []
if not root:
return result
self.traversal(root, path, result)
return result
def traversal(self, node: [TreeNode], path:list[int], result: list[str]) -> None:
path.append(node.val)
if not node.left and not node.right:
result.append('->'.join(map(str, path)))
if node.left:
self.traversal(node.left, path[:], result)
if node.right:
self.traversal(node.right, path[:], result)在 Python 中,列表是可变对象,如果直接传递列表 path,则在递归调用过程中可能会修改当前路径列表,这会导致不正确的结果。因为在递归过程中,我们会多次修改 path,而不是每次递归调用都使用相同的初始路径。
所以,为了避免这种情况,我们需要在每次递归调用时传递当前路径的副本,而不是直接传递当前路径本身。通过使用切片 path[:],我们创建了当前路径的一个副本,并将副本传递给递归调用的下一级。这样,即使在递归调用中修改了副本 path,原始的当前路径列表 path 也不会受到影响。
简而言之,传递 path[:] 会创建当前路径的一个副本,这样可以确保每次递归调用使用的路径都是独立的,避免了在递归调用过程中修改原始路径的情况。
第二种采用字符串拼接实现
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# 隐藏回溯版本(采用字符串拼接)
class Solution3:
def binaryTreePaths(self, root: [TreeNode]) -> list[str]:
path = ''
result = []
if not root: return result
self.traversal(root, path, result)
return result
def traversal(self, cur: TreeNode, path: str, result: list[str]) -> None:
path += str(cur.val)
# 若当前节点为leave,直接输出
if not cur.left and not cur.right:
result.append(path)
if cur.left:
# + '->' 是隐藏回溯
self.traversal(cur.left, path + '->', result)
if cur.right:
self.traversal(cur.right, path + '->', result)在递归调用 traversal 方法时,我们传递的是 path + '->',而不是 path 本身。这里的 path + '->' 是一个新的字符串,它在每一次递归调用中都是独立的,不会修改原始的 path 字符串。
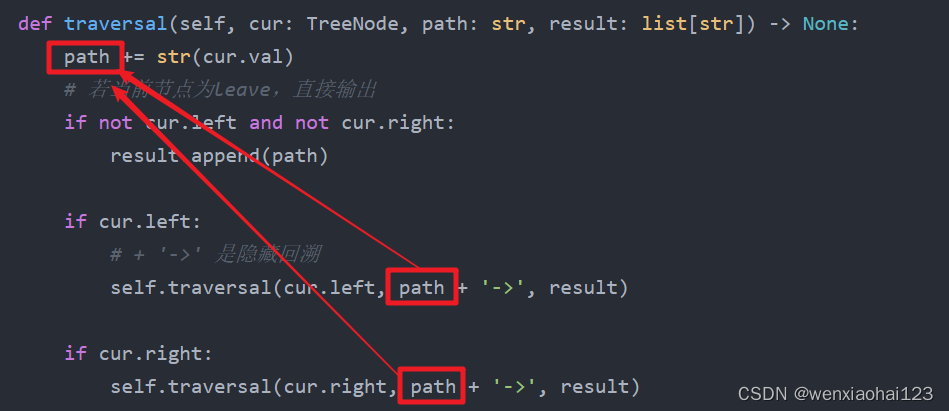
看整个代码,我们传入左右树的path依旧是当前递归中的path,并没有左节点递归的影响。通过这种方式,我们避免了在递归调用过程中修改原始的 path 字符串,从而确保了每次递归调用使用的路径都是独立的。
404.左叶子之和
题目链接:404. 左叶子之和 - 力扣(LeetCode)
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。示例:
输入:[1,2,3,None,5,None,None]
输出:["1->2->5","1->3"]
文章讲解:代码随想录 (programmercarl.com)
视频讲解:二叉树的题目中,总有一些规则让你找不到北 | LeetCode:404.左叶子之和哔哩哔哩bilibili
思路:
这题我们采用DFS中前序遍历(中左右)
递归遍历并计算左叶子节点的累加和:
我们需要一个递归函数来遍历二叉树并计算左叶子节点的累加和。这个递归函数将会是我们解决问题的核心。
在遍历的过程中,我们需要记录当前节点的值,并判断其是否为左叶子节点。
如果是左叶子节点,则将其值累加到一个变量中。
然后递归遍历左右子树,分别将左右子树的左叶子节点的值累加到上面的变量中。
返回累加和:最后,我们返回累加和作为结果。
class Solution:
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
# 入口函数,调用递归函数
return self.traversal(root)
def traversal(self, node: Optional[TreeNode]) -> int:
# 递归函数,计算左叶子节点的累加和
if not node:
return 0
left_sum = 0 # 初始化左叶子节点的累加和为0
if node.left and not node.left.left and not node.left.right:
# 如果左子节点存在且为叶子节点,则累加其值到 left_sum 中
left_sum += node.left.val
# 递归遍历左右子树,将左右子树的左叶子节点值累加到 left_sum 中
left_sum += self.traversal(node.left)
left_sum += self.traversal(node.right)
return left_sum # 返回左叶子节点的累加和感想:
这一题核心有几个要注意的地方
1.在递归函数中,确保对左右子树的遍历不会重复访问节点。
2.正确处理空节点的情况,避免出现空指针异常。
3.确保在每一级递归调用中,局部变量的值不会互相影响。
4.理解递归的返回值含义,确保递归函数的返回值是符合预期的。