上篇文章我们简单入门了动态规划（一般都是简单的上楼梯，分析数据等问题）点我跳转，今天给大家带来的是路径问题，相对于上一篇在一维中摸爬滚打，这次就要上升到二维解决问题，但都用的是动态规划思想嘛，所以大差不差，且听我慢慢道来。
还是用一样的方法，用同样的分析思路和技巧来分析问题解决问题。
路径规划
不同路径

• 状态表示
   这道题我们需要知道的是从左上角位置走到右下角位置总共有多少的路径，我们可以将问题拆分，题目中所说，机器人每次只能向下或者向右移动一步，所以我们到达右下角位置是怎么到达的呢？
  如图
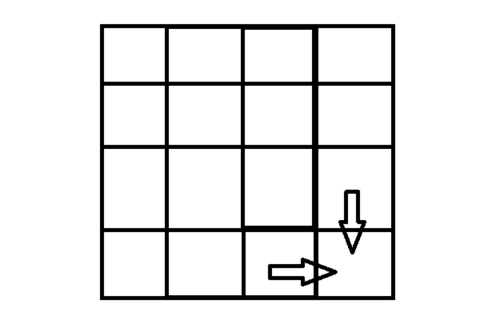  所以到达目标的方法就是到达这两个位置方法的总和。
  
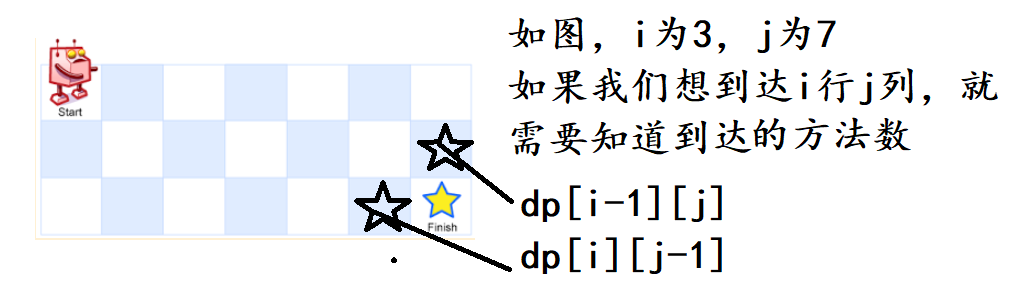
  因此这道题的状态表示就是到达ij位置总共的方法数。
• 状态转移方程
  有了上边的分析，我们可以很清晰地知道
  状态转移方程为

dp[i][j]=dp[i-1][j]+dp[i][j-1]

• 初始化
   初始化顺序即填表顺序是从左上角到右下角，但是我们应该怎么初始化呢？如果套用我们的状态转移方程，我们会发现在数租的边缘部分一定会遇到越界的情况。
  
   所以在初始化时，我们可以将数组多开一行一列，这样就可以解决越界访问的问题，如何初始化这个表格呢？我们来试着分析。
  
  其他位置全部初始化为0，这样就可以避免多开的数组影响我们后续的得到的结果。
• 填表顺序
  填表顺序就是从左上角向左下角进行填写。
• 返回值
  很简单，就是返回填表后到达i,j位置时的值即可
  接下来我们就可以根据分析出的结论写代码了。

---

class Solution {
public:
    int uniquePaths(int m, int n) {
        //new出一个二维数组，并将他们的值初始化为0
        vector<vector<int>> dp(m+1,vector<int>(n+1));//这里应该怎么给空间啊
        dp[0][1]=1;
        for(int i=1;i<=m;i++)//先填每一行
            for(int j=1;j<=n;j++)//再填每一列  
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
        
        return dp[m][n];
    }
};

这里还有一道十分相仿的题目，多了一步扩展的思维而已，尝试一下吧！
不同路径2

---

第二道题
珠宝的最高价值

 如果说上一道题对标的是上一篇中的上楼梯的方法数，那么这道题对标的就是上楼梯最小花费。
思路和上一道题目很像，一起来看一看。

• 状态表示
   同样要创建一个二维数组，到达ij位置可以拿到的珠宝价值最高，那么状态表示就是到达ij位置能拿到的最大珠宝价值，说白了就是所以路径中求和最大的一条路径。
• 状态转移方程
   移动方式和上一道题目一样，但是相比于上一道题目的相加，这道题目就是从上边或者左边到达ij位置时，他们两个谁的路径和最大。因为上一道题目已经解释很清楚了，这里就不再画图赘述。

dp[i][j]=max(dp[i-1][j],dp[i][j-1];

• 填表顺序
   从左上角向右下角。要注意是从下表为1,1位置开始填表的。
• 初始化
   初始化方式和前边那道题目大同小异，只不过我们多开的数组默认为0不用管就行，因为第一个位置只需要加上他这个位置的财宝价值即可。
• 返回值
  返回到达左下角位置能达到的最高价值数。
  我们还是直接来展示代码吧，毕竟和前边那道题很像，除了状态转移方程不同。
  代码如下

class Solution {
public:
    int jewelleryValue(vector<vector<int>>& frame) {
        int m=frame.size();
        int n=frame[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1));
        for(int i=1;i<=m;i++)
            for(int j=1;j<=n;j++)
                dp[i][j]=max(dp[i][j-1],dp[i-1][j])+frame[i-1][j-1];

        return dp[m][n];
    }
};

第三道题
下降路径最小和

 首先来进行题目解析，这道题目只需要从上到下找到最小的路径即可，而且在某位置可以向下边三个位置进行跳转。

• 状态表示
   状态表示就是到达ij位置时，需要的最小路径和，然后找出最后一行中最小的，就找到了最小路径下降和。
• 状态转移方程
  可以来画图分析一下
  
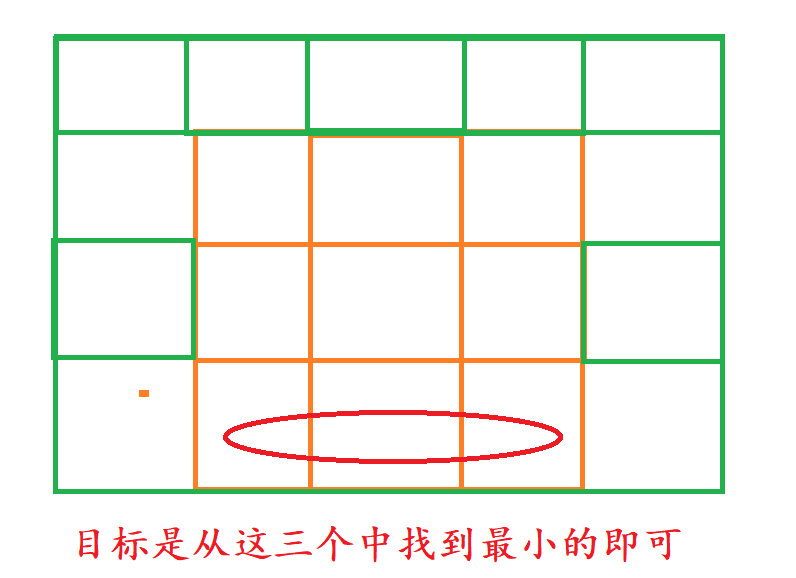
   根据我们的状态表示，我们需要找到最小路径和，只需要找到这个位置上边三种情况的最小路径和即可。
  
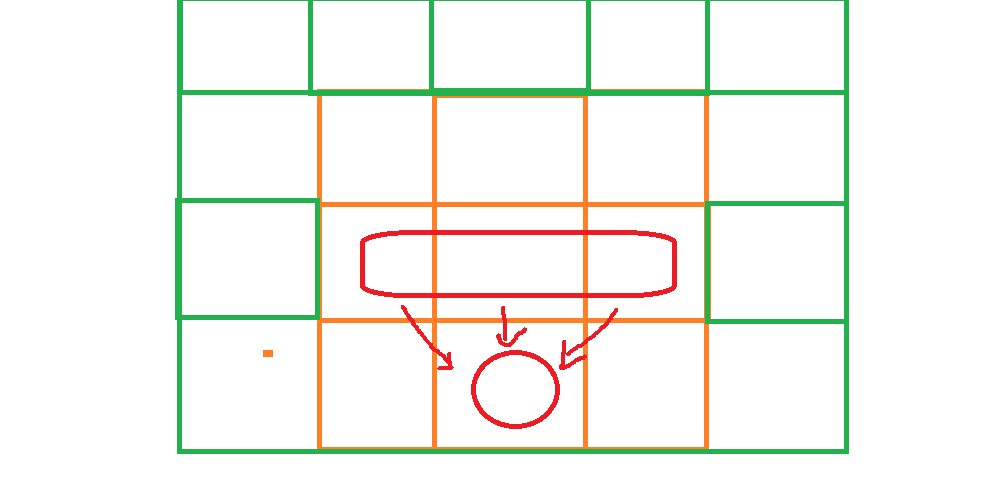
  当然，到达ij位置时，还需要加上ij位置上的值。
  故而状态转移方程为

dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j+1],dp[i-1][j]))+matrix[i-1][j-1];//要注意这里位置的对应

这里状态对应的问题后边会解释到。

• 初始化
  这里初始化是一个问题，问题在于在我们求第一行时，第一行的上边并没有数据，访问dp[-1][-1]势必会造成越界访问，如何解决呢？有了上边题目的铺垫，只需要扩展数组即可。
  相信大家已经看到了上边的画图中分别用两种颜色标记，如何初始化才能不影响后续的结果呢？
  
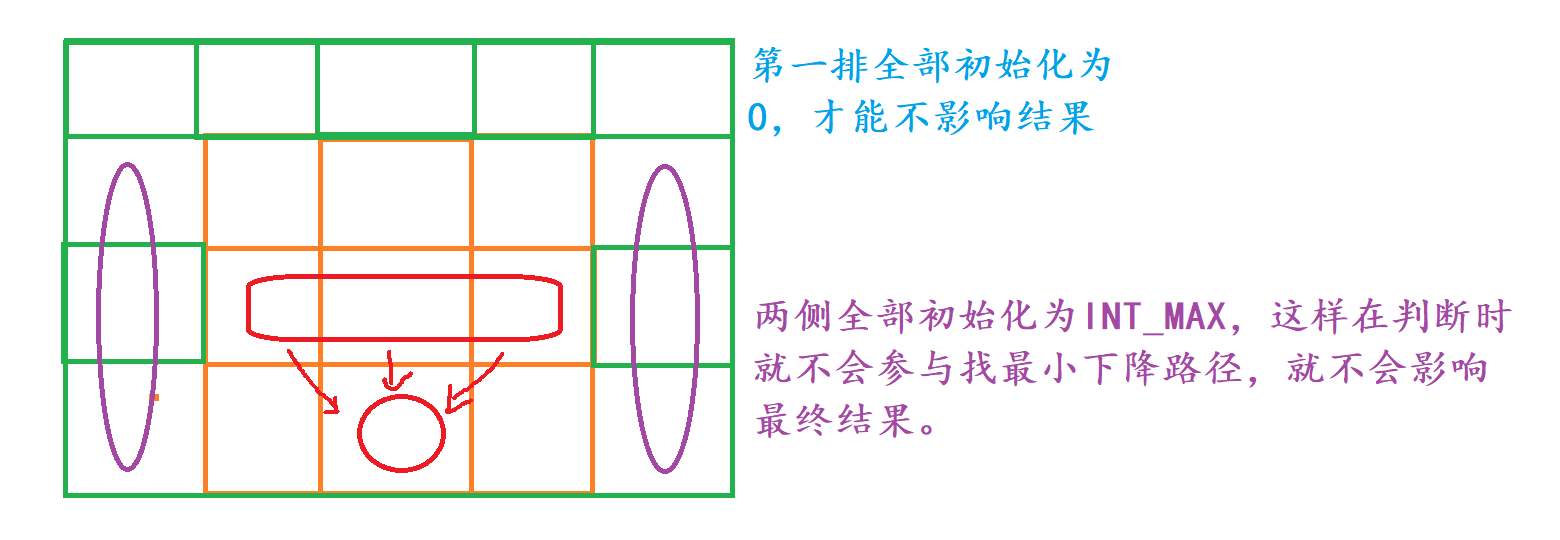
   因为这道题目的数组开的并不规则，所以对应位置容易混淆，如果你匆匆写代码的话，势必会出现这样的问题，
  
  还会出现这样的问题
  
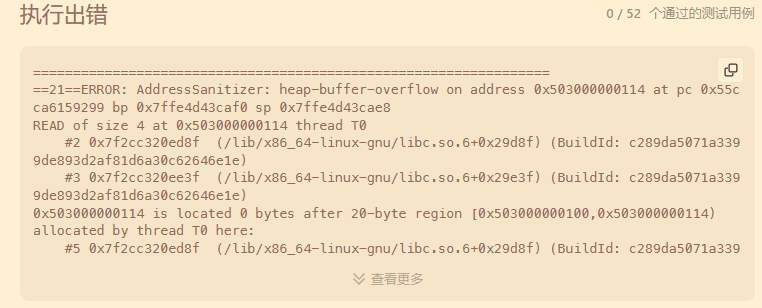
   第一种就是没有空控制好dp表的填写，导致初始化时的INT_MAX参与了运算，第二种就是因为多开两列，多开一行导致的位置判断不准确，以至于越界访问了。

• 填表顺序
  很明显，从上往下进行填表

• 返回值
   这里返回值和之前不太一样，需要找到最后一行元素中最小的一个，然后返回即可。
   代码如下，一定要尝试自己写一下，这道题是正方形表格，但是我作为长方形表格来做了，大家可以忽略这些小细节哈。

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        int m=matrix.size();
        int n=matrix[0].size();
        vector<vector<int>> dp(m+1,vector<int> (n+2,INT_MAX));
        //怎么把两边初始化为int_max;
        //cout<<int_max;
        for(int k=0;k<=n+1;k++)
        {
            dp[0][k]=0;
        }
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n+1;j++)//这里要注意，只需要初始化我们需要的部分
            {
                dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j+1],dp[i-1][j]))+matrix[i-1][j-1];//要注意这里位置的对应
            }
        }
        //此时只需找到最后一行的最小值。
        int ret=INT_MAX;
        for(int j=1;j<=n;j++)
        {
            ret=min(ret,dp[m][j]);
        }
        return ret;
    }
};

 本文到此结束，感谢大家观看，有问题及时提出，我会积极解决的。