上一节,我们讲述了二叉树的概念,二叉树又有什么基本操作呢?今天我们来讲述二叉树的应用~
话不多说,书继上回
5.3二叉树的遍历及应用
二叉树由三个基本部分组成:根结点(D),左子树(L),右子树(R)。
因此,对二叉树的遍历可以分别对这三个部分进行。
如果遵循先左后右的原则,可以有三种遍历规则:DLR,LDR,LRD。
分别称为先序遍历,中序遍历和后序遍历。
1.先序遍历
定义:若二叉树为空,则空操作,否则:
(1)访问根结点;
(2)先序遍历左子树;
(3)先序遍历右子树。
按照这个递归定义可以写出先序遍历二叉树的递归算法:
void PreOrder(BiTree T) {
if (!T) return;
visite(T->data);//访问根结点
PreOrder(T->lchild);
PreOrder(T->rchild);
}2.中序遍历
定义:若二叉树为空,则空操作,否则:
(1)中序遍历左子树;
(2)访问根结点;
(3)中序遍历右子树。
按照这个递归定义可以写出中序遍历二叉树的递归算法:
void InOrder(BiTree T) {
if (!T) return;
InOrder(T->lchild);
visite(T->data);//访问根结点
InOrder(T->rchild);
}3.后序遍历
定义:若二叉树为空,则空操作,否则:
(1)后序遍历左子树;
(2)后序遍历右子树。
(3)访问根结点;
按照这个递归定义可以写出后序遍历二叉树的递归算法:
void PostOrder(BiTree T) {
if (!T) return;
PostOrder(T->lchild);
PostOrder(T->rchild);
visite(T->data);//访问根结点
}可见这三种遍历的搜索路线是一样的,只是访问根的时机不同。
将二叉树上每个空子树用一个虚结点表示,将这样处理后的二叉树称为原二叉树的扩展二叉树。
原二叉树上的结点称为内部结点,表示空指针的虚结点称为外部结点。
递归算法优点是简洁,但一般而言,其执行效率不高,因为系统需要维护一个运行栈以保证递归过程是正确执行。其实以上遍历还可以使用非遍历方法。
设一存放结点指针的栈S,每访问完一个结点X后,就将结点X的指针入栈,以便后来能通过这个指针找到结点X的右子树。
void PreOrder(BiTree T) {
InitStack(S); //初始化一个空栈
while (T || !StackEmpty(S)) {//遍历结束的条件是栈为空且T为空
while (T) {
visite(T->data);
Push(S, T); //T进栈
T = T->lchild;
}
if (!StackEmpty(S)) {
Pop(S, T); //弹出栈顶指针T
T = T->rchild;
}
}
}其中有关栈的处理(其中一些函数)详见前面的文章
附链接:【数据结构】五分钟自测主干知识(四)http://t.csdnimg.cn/DffSW![]() http://t.csdnimg.cn/DffSW
http://t.csdnimg.cn/DffSW
4.层序遍历
对二叉树除了可以按上述的先序、中序和后序规则进行遍历外,还可以自上而下,自左向右逐层地进行遍历。
在层序遍历时,当第 i 层结点被访问完后,接下来要逐个访问位于第i + 1 层上的第 i 层结点的左孩子和右孩子。这时,在 i层先被访问的结点其左、右孩子将先被访问,因此需要利用一个队列来存放已访问过的结点的孩子,以控制对这些孩子的访问先后次序。层序遍历的算法思路是:
(1)初始化一个空队列,用来保存已访问过结点的孩子;
(2)非空根指针入队;
(3)若队列为空,则遍历结束;否则重复执行:
①队头元素出队,访问之;
②若被访结点有左孩子,则左孩子入队;
③若被访结点有右孩子,则右孩子入队。
void LayerTraversal(BiTree T) {
InitQueue(Q);
if (T) EnQueue(Q, T);
while (!QueueEmpty(Q)) {
DeQueue(Q, p);
visite(p->data);
if (p->lchild) EnQueue(Q, p->lchild);
if (p->lchild) EnQueue(Q, p->rchild);
}
}其中有关队列的处理(其中一些函数)详见前面的文章
附链接:【数据结构】五分钟自测主干知识(五)
http://t.csdnimg.cn/TX4HA![]() http://t.csdnimg.cn/TX4HA
http://t.csdnimg.cn/TX4HA
不论按哪种次序遍历含有n个结点的二叉树,其时间复杂度至少为
。
5.二叉树运算举例
1.求二叉树的结点个数
方案1:
int CountNodes1(BiTree T) {
if (!T) return 0;
int nl = CountNodes1(T->lchild);
int nr = CountNodes1(T->rchild);
return(1 + nl + nr);
}方案2:
void CountNodes2(BiTree T, int& n) {
if (!T)return;
n++;
CountNodes2(T->lchild, n);
CountNodes2(T->rchild, n);
}2.输出二叉树每个结点的层次数
void Level(BiTree T, int lev){
if (!T)return;
lev++;
printf(T->data,lev);
Level(T->lchild, lev);
Level(T->rchild, lev);
}3.求二叉树的深度
好用的递归方法继续:
int Depth(BiTree T) {
if (!T)return 0;
int hl = Depth(T->lchild);
int hr = Depth(T->rchild);
return (hl > hr ? hl + 1: hr + 1);
}4.输出二叉树树根到所有叶子结点的路径
void OutPath(BiTree T, Stack& S) {
if (!T)return;
Push(S, T);
if (!T->lchild && !T->rchild)
StackTraverse(S);
OutPath(T->lchild, S);
OutPath(T->rchild, S);
Pop(S, e);
}5.(重点)表达式求值
算术表达式可以用二叉树的形式来表示。
用二叉树表示算术表达式的递归方法如下:
(1)如果表达式为常数或简单变量,则二叉树中仅有一个根结点,根结点的数据域存放该表达式的值。
(2)如果表达式的形式是:
(左操作数) 二目运算符 (右操作数)
则二叉树中,以左子树表示左操作数,右子树表示右操作数,根结点的数据域存放二目运算符。
(3)操作数本身又是表达式
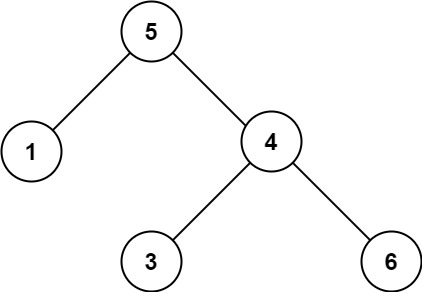
例如表达式的二叉树表示如下:
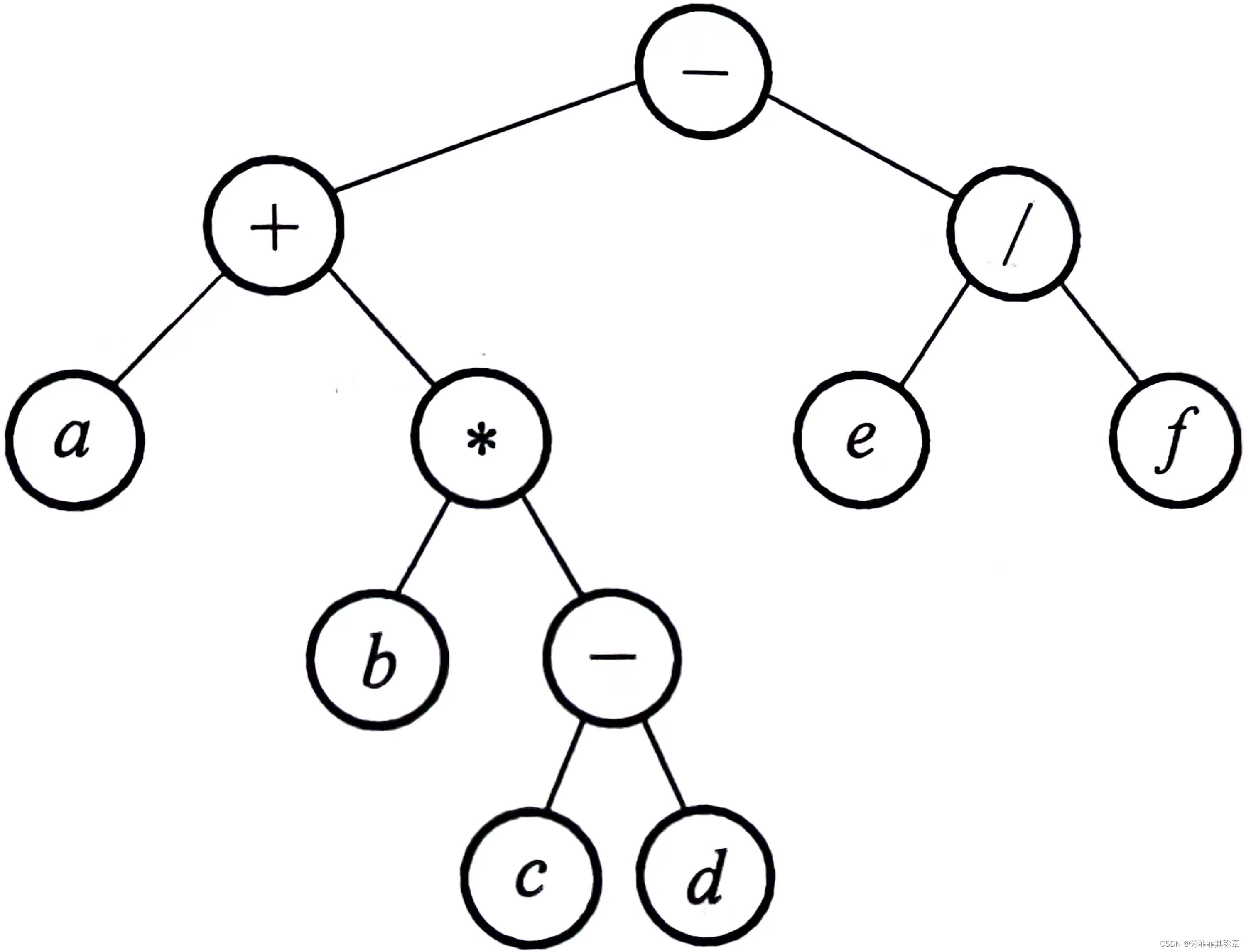
该二叉树的先序序列为
恰好是表达式的前缀表示(波兰式)
该二叉树的后序序列为
恰好是表达式的后缀表示(逆波兰式)
下面给出表达式二叉树结点的存储类型定义:
typedef struct BiNode {
double val;
char op;
unsigned char tag;
struct BiNode* lchild, * rchild;
}BiTNode,*BiTree;其中val分量用来存放表达式中的数值,op分量用来存放表达式中的运算符。
tag起标志作用,若tag=0,则表示结点中存放的是数值,取val分量;
若tag=1,则表示结点中存放的是运算符,取op分量。
对表达式求值可用逆波兰式的求值方法,即利用后序遍历完成计算
double Calculate(BiTree T) {
if (T->tag == 0)return T->val;
double a = Calculate(T->lchild);
double b = Calculate(T->rchild);
return operate(a, T->op, b);//计算并返回a op b
}其中operate函数表示计算算式值
今天我们就到这里,可以对照黑体字查看主干知识,下一讲,我们聊聊线索二叉树
附链接:【数据结构】五分钟自测主干知识()
长咕一下