堆的特征

1.堆是一个完全二叉树

2.堆分为大堆和小堆。大堆：左右节点都小于根节点

小堆：左右节点都大于根节点

堆的应用：堆排序，topk问题

堆排序

堆排序的思路：

1.升序排序，建小堆。堆顶就是这个堆最小的数，堆顶和这个堆的最后一个数换位置，然后再把最后一个数取出，再pop这个数。就得到最小值。像这样每次取一个最小值，再删掉。依次把取出的数放在数组中，就得到升序排序了。

2.降序排序，建大堆。思路同升序一样。

上面说的是向下调整。向下调整就是每次取个数，由于和堆的最后一个数交换了位置，取出之后的二叉树需要调整一下才能成为一个堆。如果是大堆，就比较堆顶的和左右子树，大于它，堆顶和大的那个交换，这样层层交换下去。

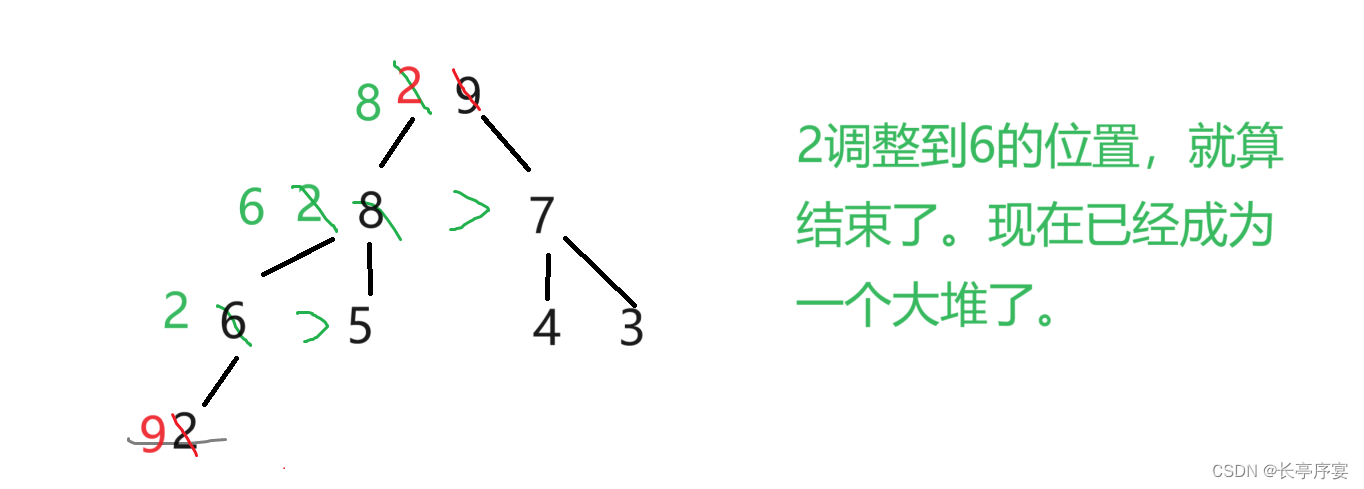
如果一共有k层，最坏交换k次，如果是N个节点，就是log(N+1)次。

堆排序就是排N个数嘛，时间复杂度就是O(N*logN)，空间复杂度就是O(N)。

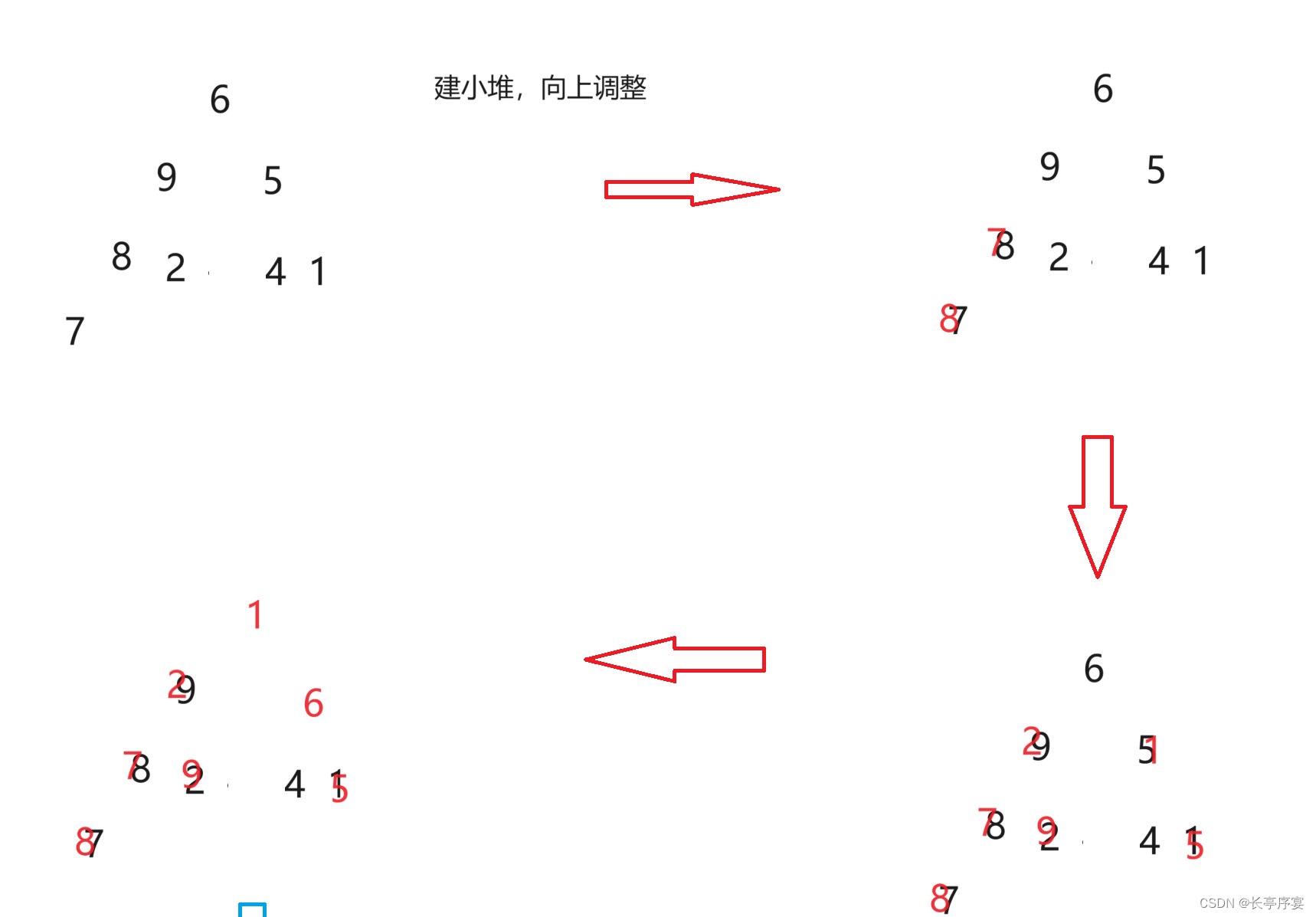
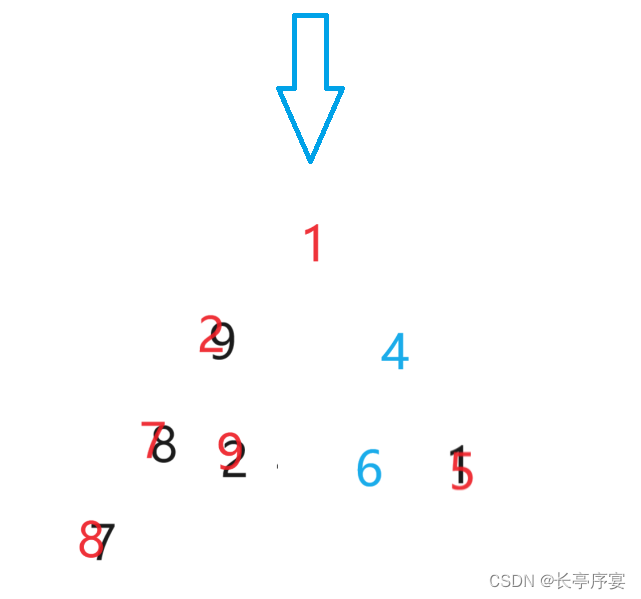
向上调整：

向上调整可以应用于尾部插入数。调成一个大堆后停止。

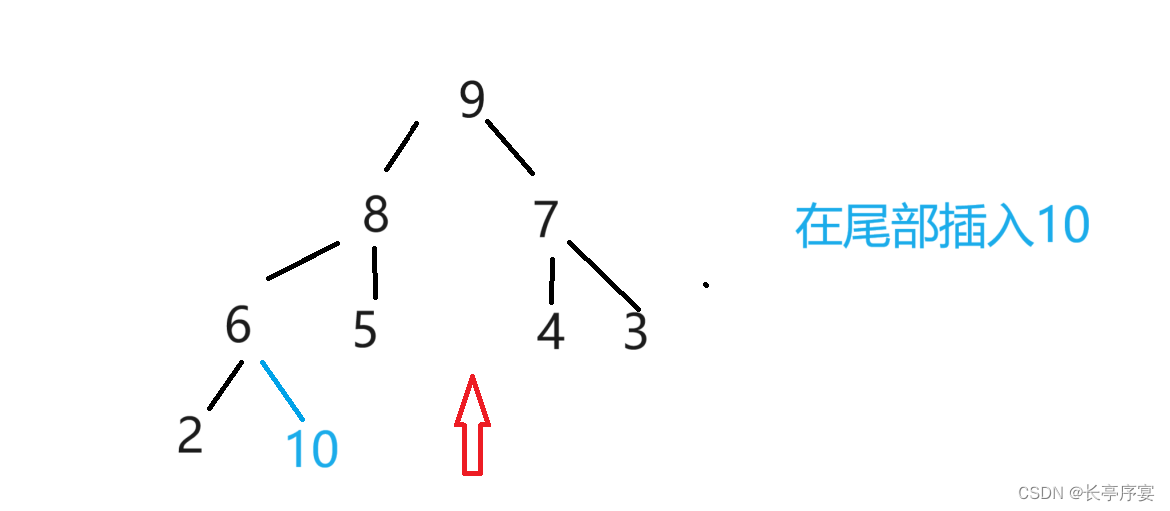
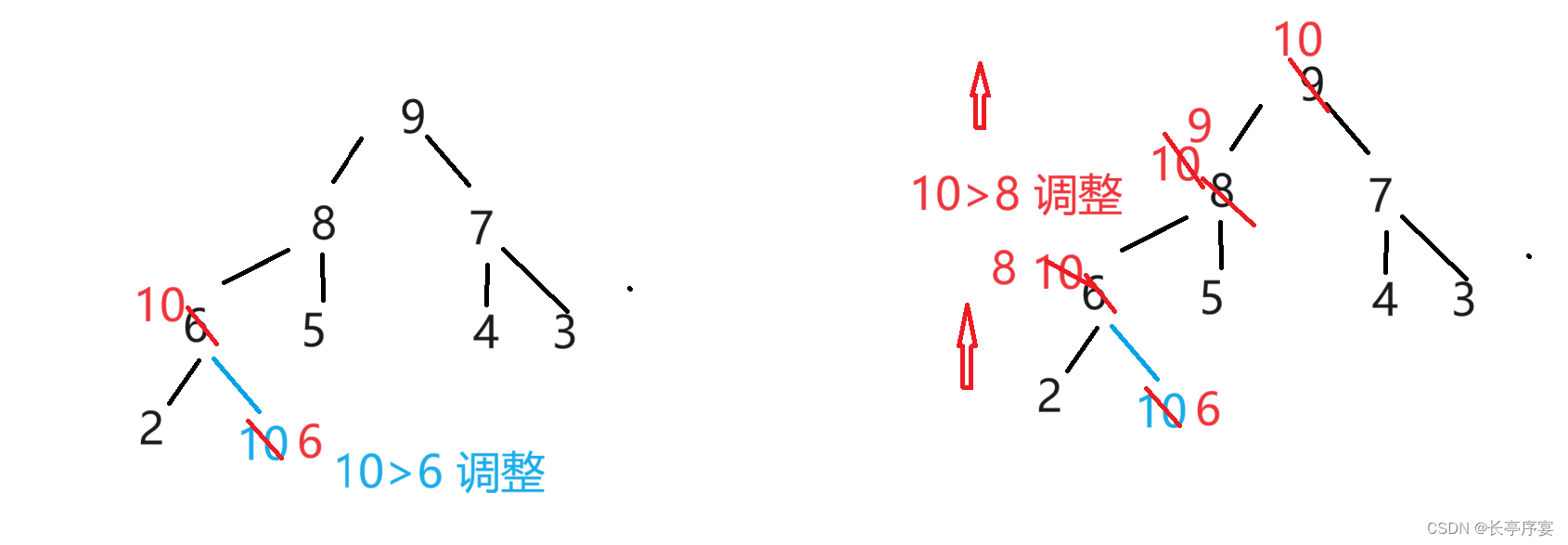
对于一个随机数组，建大堆，向下调整法：

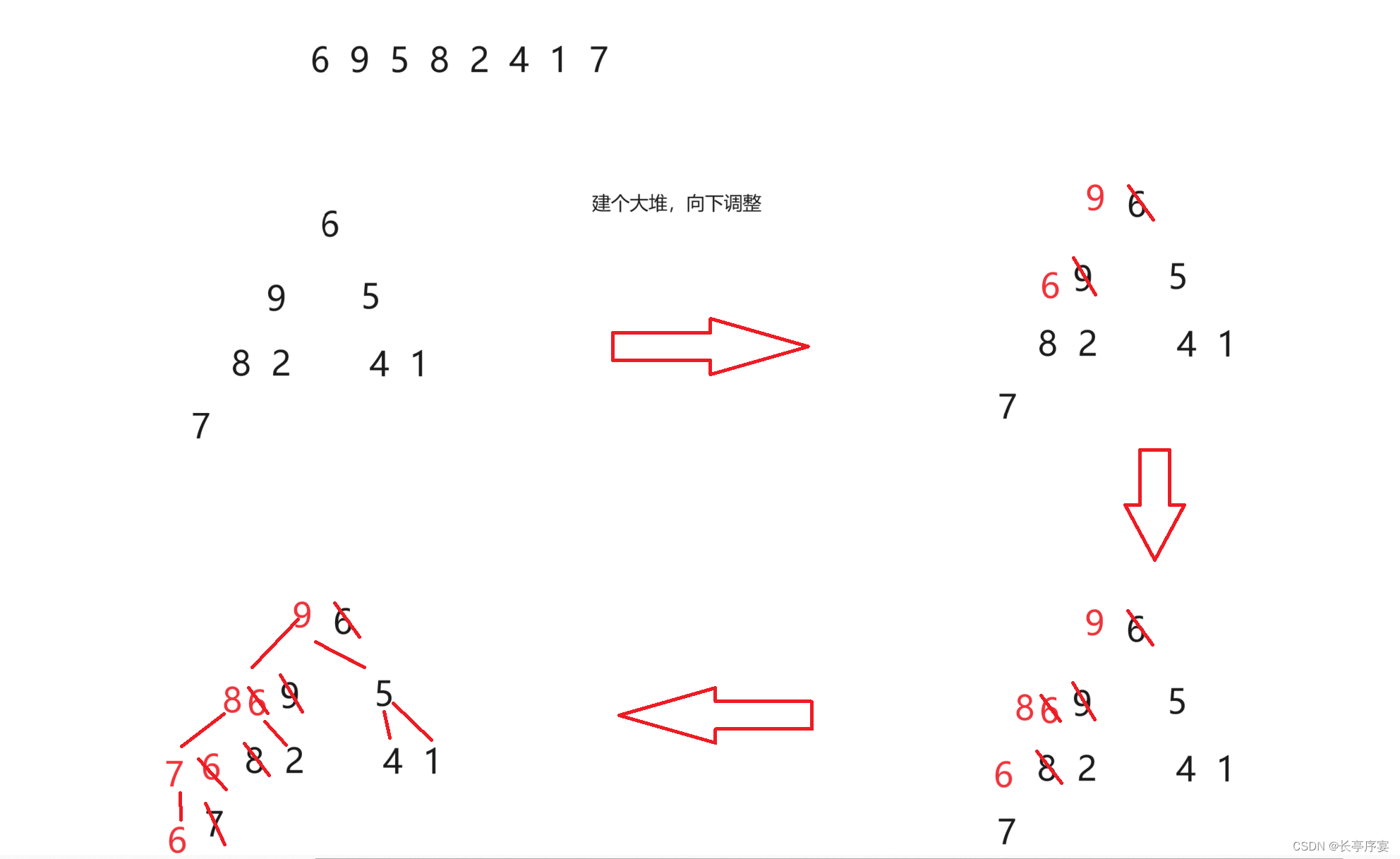
对于一个随机数组建小堆，向上调整法：

topk问题

如何从10000个数中取出最大的50个数？此问题也可以用于：内存空间不够，建堆数量有限，如何在大量的数据中取出前k个最大（小）的数。

答：先取出这些数据中前50(k)个建小堆，剩下的数和堆顶相比，遇到大于堆顶的数就直接替换掉堆顶的数。替换一次，小堆也要向下调整一次，保持它是一个小堆。这样比到最后一个数。就能保持这个小堆是这10000个数中最大的50个了。

如果是取出最小的50个数，那就是建大堆了。遇到比堆顶小的就替换、调整等。

二叉树的遍历

用链表建二叉树。

typedef struct BinaryNode
{
    int val;
    struct BinaryNode* left;
    struct BinaryNode* right;
}BTNode,*pBTNode;

如上述代码所示，树的一个节点存储三个值，一个是它的数据，一个是它指向的左子树指针，一个是指向右子树的指针。如果左子树和右子树都是空，就指向空。

这样由链表构建的一个二叉树。可以通过三种遍历方式来读取整个二叉树的数据。

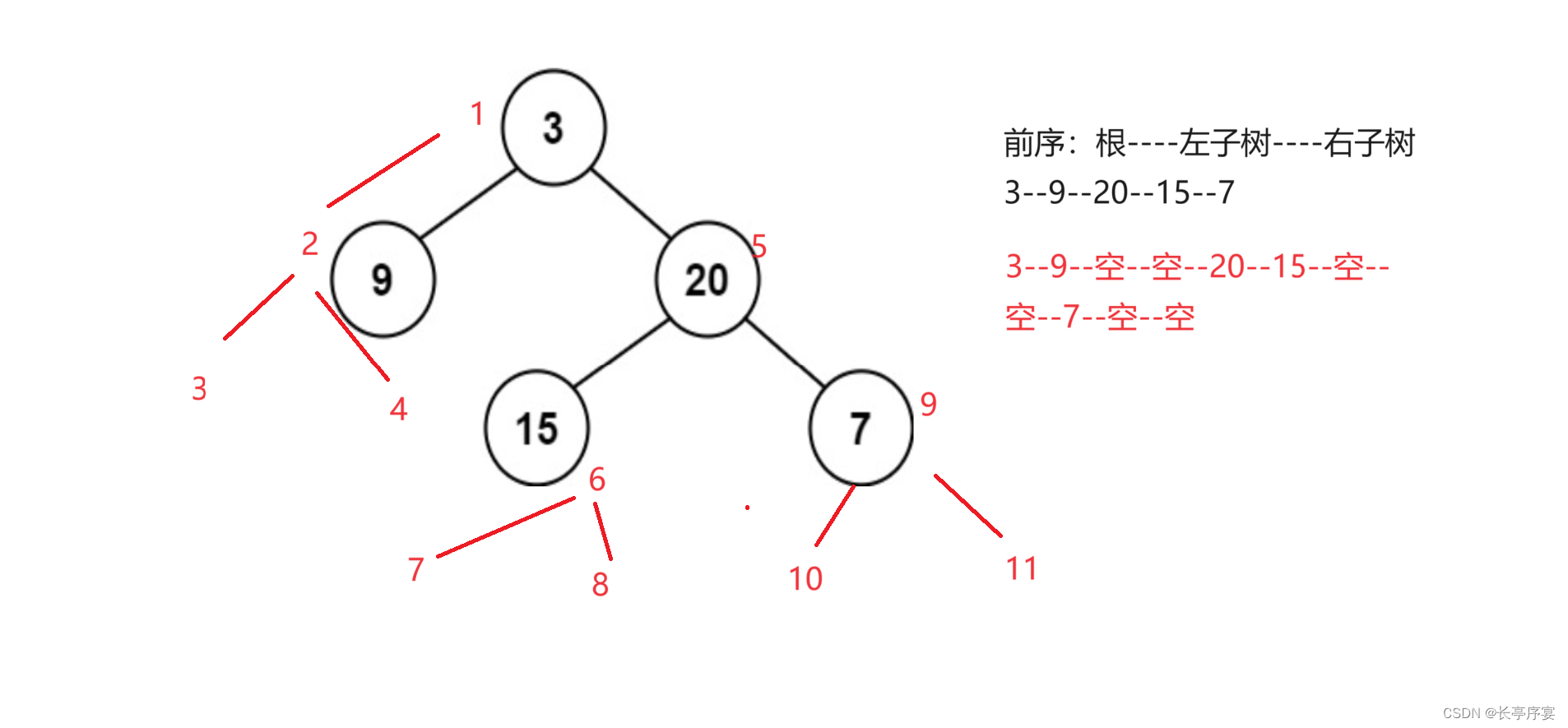
前序：根----左子树----右子树

中序：左子树----根----右子树

后序：左子树----右子树----根

前中后序的命名是根据访问根的顺序来命名的。以前序遍历来举例：