基础思想 :
介绍
线段树可以用来维护区间信息(区间和 , 区间最值 , 区间GCD等) ,可以在log n的时间内执行区间修改 和 区间查询 ;
1 . 叶子结点的特点是左右结点相等 , 存储元素本身;
2 . 非叶子结点存储的是区间内的统计值 ,
建树
建树的过程相当于dfs :
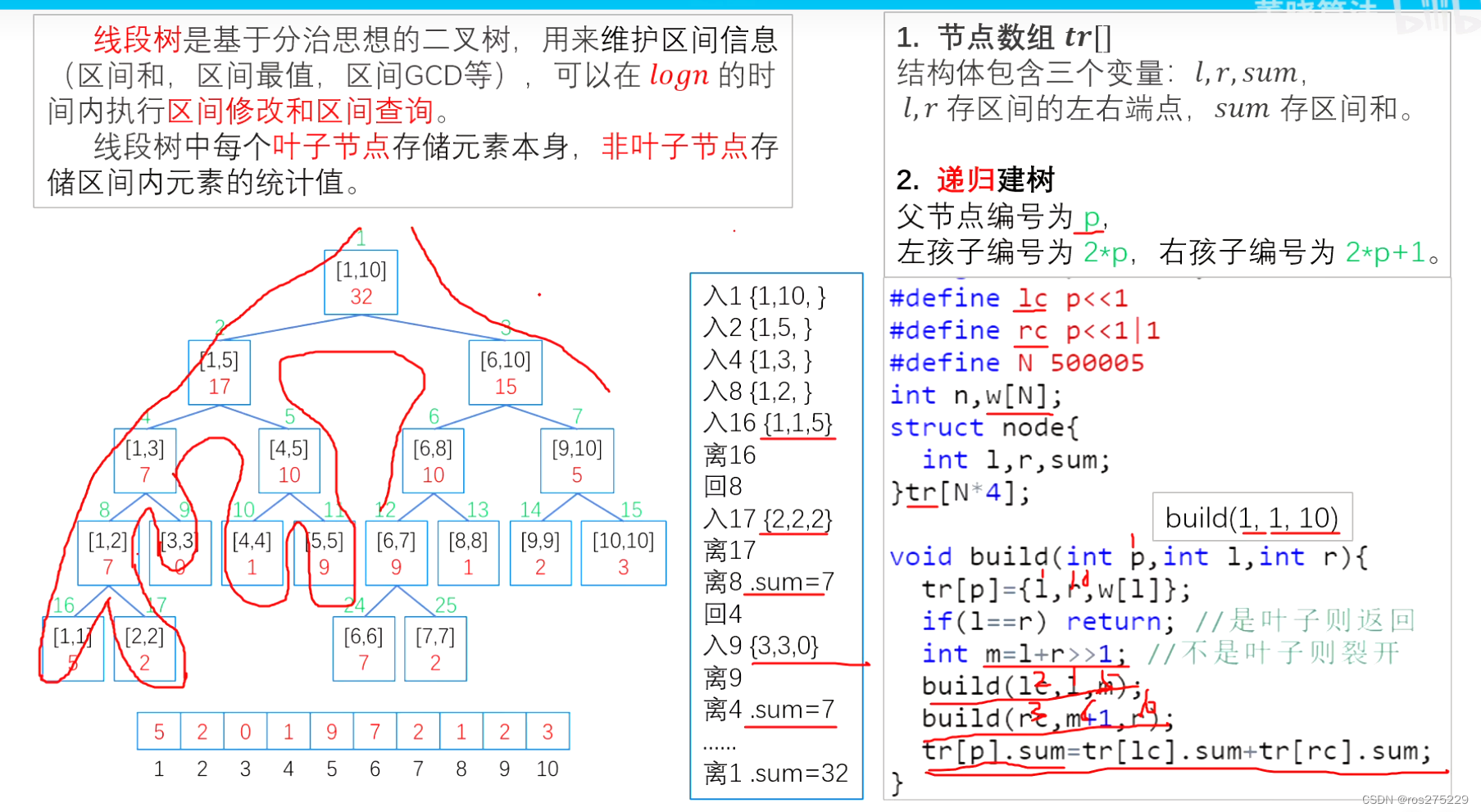
#define lc p<<1 ;
#define rc P<<|1 ;
#define N 5e5 + 10 ;
int n , w[N] ;
struct node{
int l , r , sum , add ;
}tr[N*4];
// 建树
void build(int p , int l , int r){
// 对 [l,r] 区间建立线段树 ,当前根的编号为 p
tr[p] = {l , r , w[l]} ;
if(l==r) return ; // 是叶子结点就返回
int m = l + ((r-l)>>1);
build(lc,l,m) ;
build(rc,m+1,r);
tr[p].sum = tr[lc].sum + tr[rc].sum ;
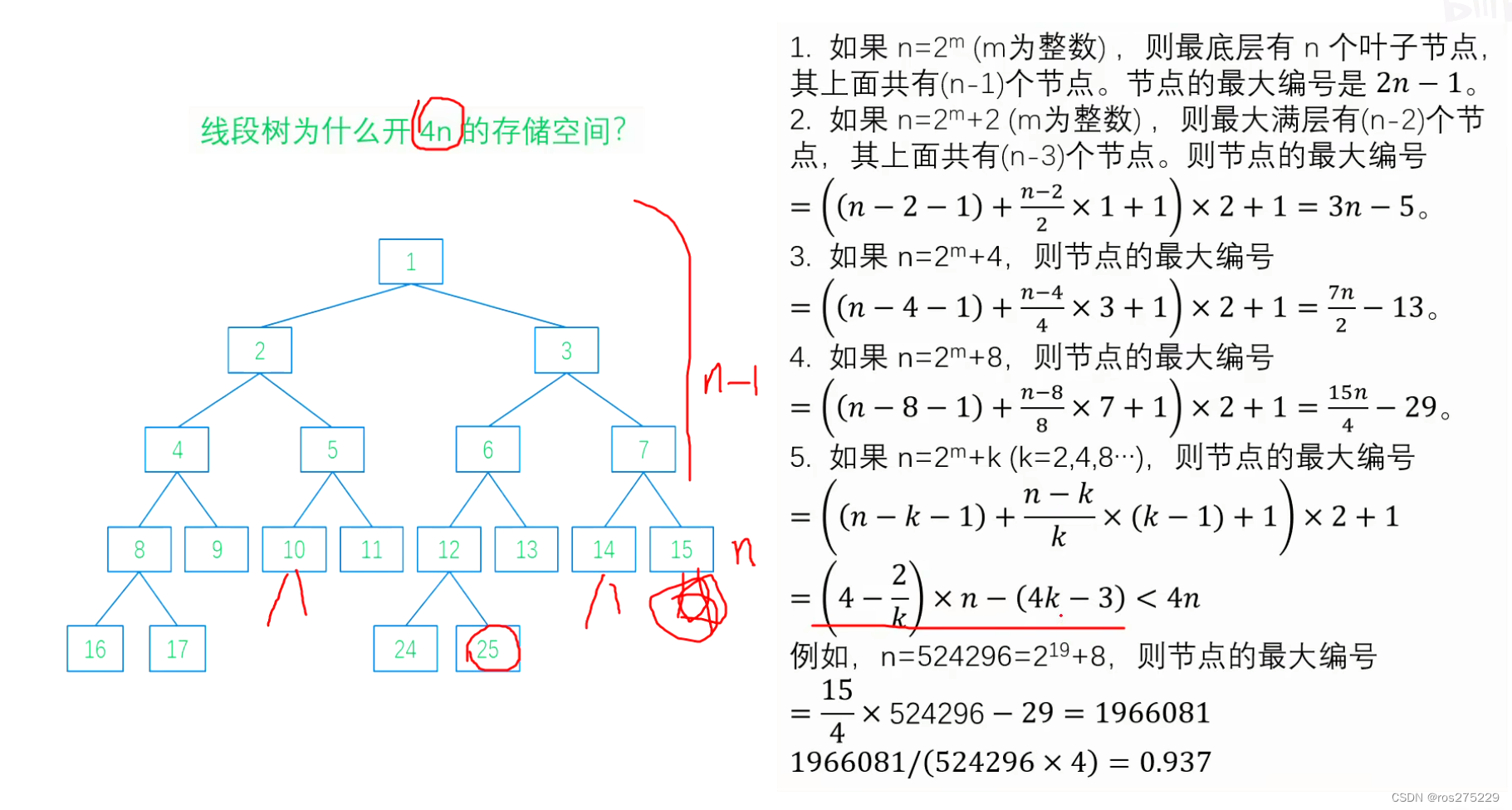
}为什么要开N*4的存储空间 :
点修改 :

// 点修改
void update(int p,int x , int k){ // 点修改 : 对点x加上k : O(logn)
// 从根节点出发,递归找到叶子节点,然后从下往上更新其祖先结点
if(tr[p].l==x && tr[p].r==x){ // 叶子结点
tr[p].sum += k ;
return ;
}
int m = tr[p].l + ((tr[p].r-tr[p].l)>>1) ;//非叶子结点则裂开
if(x<=m) udate(lx,x,k) ;
if(x>m) update(rc,x,k) ;
tr[p].sum = tr[lc].sum + tr[rc].sum ;
} 区间查询 :

// 区间查询
int query(int p,int x,int y){ // 查询区间[x,y]的和 : O(logn)
if(x<=tr[p].l&&tr[p].r<=y){
return tr[p].sum ;
}
int m = tr[p].l + ((tr[p].r-tr[p].l)>>1) ;
int sum = 0 ;
if(x<=m) sum += query(lc,x,y);//与左区间重叠
if(y>m) sum += query(rc,x,y);//与右区间重叠
return sum ;
}如果带上懒标记 :
// 区间查询
int query(int p,int l,int r){ // 查询区间[x,y]的和 : O(logn)
if(l<=tr[p].l&&tr[p].r<=r){
return tr[p].sum ;
}
pushdown(p) ;
int m = tr[p].l + tr[p].r >> 1 ;
int sum = 0 ;
if(l<=m) sum += query(lc,l,r);//与左区间重叠
if(r>m) sum += query(rc,l,r);//与右区间重叠
return sum ;
}区间修改 :
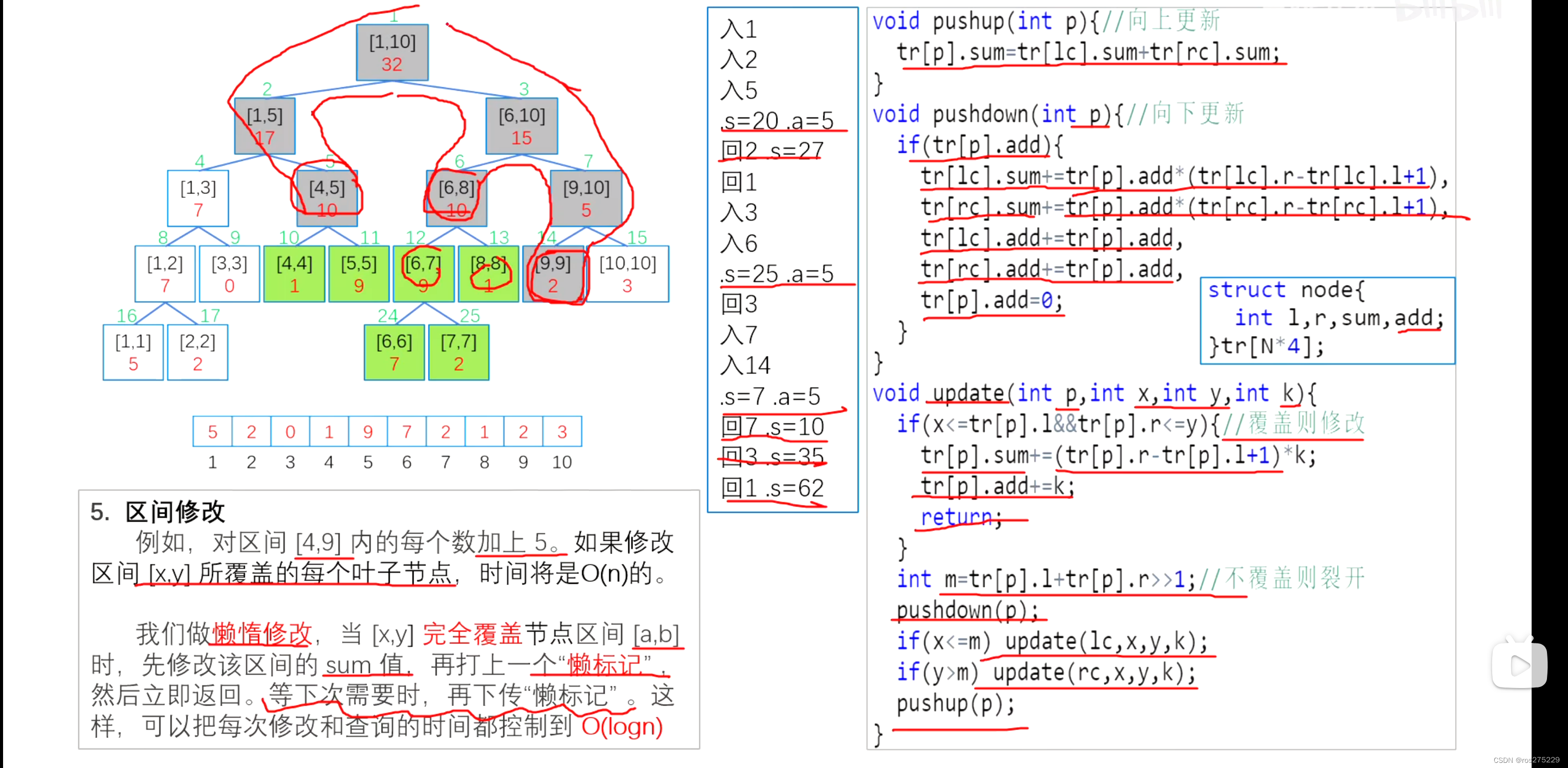
// 区间修改
void pushup(int p){// 向上更新
tr[p].sum=tr[lc].sum+tr[rc].sum;
}
void pushdown(int p){ // 向下更新
if(tr[p].add){
tr[lc].sum+=tr[p].add*(tr[lc].r-tr[lc].l+1),
tr[rc].sum+=tr[p].add*(tr[rc].r-tr[rc].l+1),
tr[lc].add+=tr[p].add,
tr[rc].add+=tr[p].add,
tr[p].add=0;
}
}
void updateQJ(int p,int x,int y,int k){//对[x,y]全部+k
// 先走到叶子节点,将每个叶子节点+k,然后返回修改祖先的结点
// 做懒惰标记,当区间[x,y]完全覆盖[a,b],先修改区间的sum值,再打上一个懒标记,然后立即返回
// 等下次需要是,再下传懒标记,这样就可以将每次修改和查询的时间都控制在O(logn);
if(x<=tr[p].l&&tr[p].r<=y){//覆盖则修改
tr[p].sum += (tr[p].r-tr[p].l+1)*k;
tr[p].add+=k;
return ;
}
int m = tr[p].l + ((tr[p].r-tr[p].l)>>1) ;
pushdown(p);
if(x<=m) update(lc,x,y,k) ;
if(y>m) update(rc,x,y,k) ;
pushup(p);
}例题 :
【模板】线段树 1 - 洛谷
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
const int N = 1e5 + 10 ;
#define lc p<<1
#define rc p<<1|1
int w[N] ;
struct Tree{
int l , r , sum , add ;
}tr[N*4];
// 区间修改
void pushup(int p){// 向上更新
tr[p].sum=tr[lc].sum + tr[rc].sum;
}
void pushdown(int p){ // 向下更新
if(tr[p].add>0){
tr[lc].sum+=tr[p].add*(tr[lc].r-tr[lc].l+1);
tr[rc].sum+=tr[p].add*(tr[rc].r-tr[rc].l+1);
tr[lc].add+=tr[p].add;
tr[rc].add+=tr[p].add;
tr[p].add=0;
}
}
// 建树
void build(int p , int l , int r){
// 对 [l,r] 区间建立线段树 ,当前根的编号为 p
tr[p] = {l , r , w[l],0} ;
if(l==r) return ; // 是叶子结点就返回
int m = l + r >> 1 ;
build(lc,l,m) ;
build(rc,m+1,r);
pushup(p) ;
}
void updateQJ(int p,int l,int r,int k){//对[l,r]全部+k
// 先走到叶子节点,将每个叶子节点+k,然后返回修改祖先的结点
// 做懒惰标记,当区间[l,r]完全覆盖[a,b],先修改区间的sum值,再打上一个懒标记,然后立即返回
// 等下次需要是,再下传懒标记,这样就可以将每次修改和查询的时间都控制在O(logn);
if(l<=tr[p].l&&tr[p].r<=r){//覆盖则修改
tr[p].sum += (tr[p].r-tr[p].l+1)*k;
tr[p].add+=k;
return ;
}
int m = tr[p].l + tr[p].r >> 1 ;
pushdown(p);
if(l<=m) updateQJ(lc,l,r,k) ;
if(r>m) updateQJ(rc,l,r,k) ;
pushup(p);
}
// 区间查询
int query(int p,int l,int r){ // 查询区间[x,y]的和 : O(logn)
if(l<=tr[p].l&&tr[p].r<=r){
return tr[p].sum ;
}
pushdown(p) ;
int m = tr[p].l + tr[p].r >> 1 ;
int sum = 0 ;
if(l<=m) sum += query(lc,l,r);//与左区间重叠
if(r>m) sum += query(rc,l,r);//与右区间重叠
return sum ;
}
// 点修改
void update(int p,int x , int k){ // 点修改 : 对点x加上k : O(logn)
// 从根节点出发,递归找到叶子节点,然后从下往上更新其祖先结点
if(tr[p].l==x && tr[p].r==x){ // 叶子结点
tr[p].sum += k ;
return ;
}
int m = tr[p].l + ((tr[p].r-tr[p].l)>>1) ;//非叶子结点则裂开
if(x<=m) update(lc,x,k) ;
if(x>m) update(rc,x,k) ;
tr[p].sum = tr[lc].sum + tr[rc].sum ;
}
signed main(){
int n , m ; cin >> n >> m ;
for(int i=1;i<=n;i++) cin >> w[i] ;
build(1,1,n);
for(int i=1;i<=m;i++){
int op ; cin >> op ;
if(op==1){
int x , y , k ; cin >> x >> y >> k ;
updateQJ(1,x,y,k) ;
}else{
int x , y ; cin >> x >> y ;
int ans = query(1,x,y);
cout << ans << endl ;
}
}
}
参考 :
线段树 - OI Wiki
C02【模板】线段树+懒标记 Luogu P3372 线段树 1_哔哩哔哩_bilibili