---------------🎈🎈42. 接雨水 题目链接🎈🎈-------------------

解法1 前后缀分解

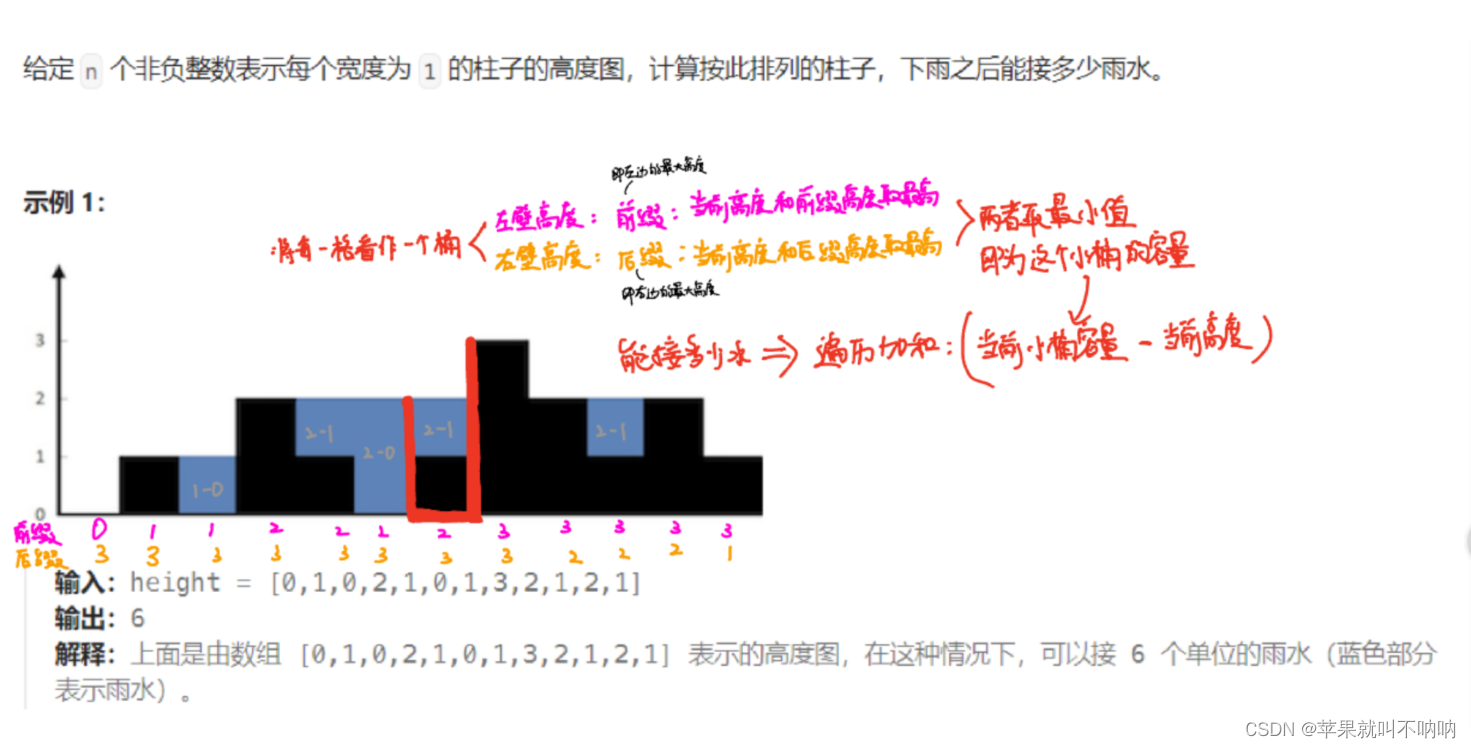
维护一个前缀（左侧最高）后缀（右侧最高）数组
把每一个小区间看做一个桶，桶的容量取决于左右壁中最低的那一个Min（leftmax，rightmax）
左壁就是当前这块及其左侧高度的最大值：前缀 leftmax
右壁就是当前这块及其右侧高度的最大值：后缀 rightmax
最终能装的水 = 当前小桶的容量-当前小柱子高度

时间复杂度O(N)
空间复杂度O(N)

class Solution {
    public int trap(int[] height) {
        // 把每一个小区间看做一个桶，桶的容量取决于左右壁中最低的那一个Min（leftmax，rightmax）
        // 左壁就是当前这块及其左侧高度的最大值：前缀 leftmax
        // 右壁就是当前这块及其右侧高度的最大值：后缀 rightmax
        // 能装的水 = 桶容量-柱子高度

        int[] leftmax = new int[height.length]; // 左边的最大高度
        int[] rightmax = new int[height.length]; // 右边的最大高度
        int templeftmax = 0;
        for(int i = 0; i < height.length;i++){ // 前缀数组
            if(height[i] > templeftmax){
                templeftmax = height[i];
            }
            leftmax[i] = templeftmax;
        }

        int temprightmax = 0;
        for(int i = height.length-1; i >=0;i--){ // 后缀数组
            if(height[i] > temprightmax){
                temprightmax = height[i];
            }
            rightmax[i] = temprightmax;
        }

        int totalWater = 0;
        // 同时遍历前后缀数组，两者取取Min即为桶内可以容纳的高度。之后减去筒高度即为水的高度，累加即可
        for(int i = 0; i< height.length; i++){
            totalWater += Math.min(leftmax[i],rightmax[i])-height[i];
        }
        return totalWater;
    }
}   

解法2 双指针

多做做吧 不行就看看动图

双指针法👿
while（left<right）
每次更新前缀最大值和后缀最大值
⭐️当 前缀最大值 < 后缀最大值时：当前的桶容量肯定为前缀最大值
⭐️当 后缀最大值 < 前缀最大值时：当前的桶容量肯定为后缀最大值
之后就更新totalwater = 当前桶容量- 底部高度即可

时间复杂度O(N)
空间复杂度O(1)⭐️⭐️

class Solution {
    public int trap(int[] height) {
        int totalWater = 0;
        // 初始化双指针 一个指头一个指尾
        int left = 0;
        int right = height.length-1;
        // 前缀最大值和后缀最大值
        int preMax =0;
        int backMax = 0;
        
        // 双指针left< right遍历
        while(left < right){
            // 更新前缀最大值和后缀最大值
            preMax = Math.max(preMax, height[left]);
            backMax = Math.max(backMax, height[right]);
            // 1.当：前缀最大值 小于 后缀最大值：说明桶容量一定为前缀最大值！！！
            if(preMax < backMax){
                totalWater += (preMax-height[left]);  // 计算totalwater = 桶容量-柱子高度
                left++;
            }
            // 2.当：后缀最大值 小于 前缀最大值：说明桶容量一定为后缀最大值！！！
            if(preMax >= backMax){
                totalWater += (backMax-height[right]);  // 计算totalwater = 桶容量-柱子高度
                right--;
            }
            // 3.前缀最大值和后缀最大值相等的时候，随便归入一类就行
        }
        return totalWater;

    }
}