多处最优服务次序问题

题目描述

设有n个顾客同时等待一项服务。顾客i需要的服务时间为ti, 1≤i≤n。共有s处可以提供此项服务。应如何安排n个顾客的服务次序才能使平均等待时间达到最小? 平均等待时间是n个顾客等待服务时间的总和除以n。
算法设计：对于给定的n个顾客需要的服务时间和s的值，计算最优服务次序。

输入描述

第一行有2 个正整数n和s，表示有n个顾客且有s处可以提供顾客需要的服务。接下来的1行中，有n个正整数，表示n个顾客需要的服务时间。

输出描述

将计算出的最小平均等待时间输出

样例

输入
10 2
56 12 1 99 1000 234 33 55 99 812
输出
336

---

思路：贪心策略，先将顾客所需服务时间按升序排序，因为要先服务所需时间少的顾客，才能是整体的平均等待时间最短（最短作业优先调度算法-SJF），每一次任务调度，都选择当前所有服务窗口中服务时间总和最短的窗口，这样当前任务所等待的时间才最少，以局部最少达到全局最少。

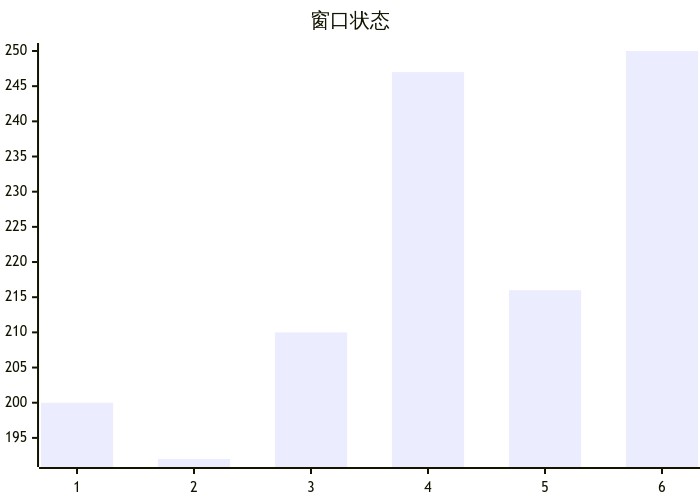
假设某时刻窗口状态如下：则下一个顾客要想等待的时间最少，那么应选择窗口2（等待时长192），所有顾客的选择策略（贪心）也均是如此。

---

Code:

#include<bits/stdc++.h>
using namespace std;
const int INF = 1e9 + 10;
const int N = 1e5 + 10;

int ms[N],t[N];
int n,s;
struct cmp {
	bool operator()(pair<int,int>&a,pair<int,int>&b) {
		return a.first>b.first;
	}
};

int main() {
	cin>>n>>s;
	for(int i=1; i<=n; i++) cin >> t[i];
	sort(t+1,t+1+n);
	priority_queue<pair<int,int>,vector<pair<int,int>>,cmp> q; //维护窗口状态
	for(int i=1; i<=s; i++) q.push({0,i});
	double sum=0;
	for(int i=1; i<=n; i++) {
		int id = q.top().second;
		q.pop();
		ms[id]+=t[i];
		sum+=ms[id];
		q.push({ms[id],id});
	}
	
	cout<<sum/n;
	
	return 0;
}

/*


*/