753. 破解保险箱

题目描述

有一个需要密码才能打开的保险箱。密码是 n 位数, 密码的每一位是 k 位序列 0, 1, ..., k-1 中的一个。

你可以随意输入密码，保险箱会自动记住最后 n 位输入，如果匹配，则能够打开保险箱。

举个例子，假设密码是 “345”，你可以输入 “012345” 来打开它，只是你输入了 6 个字符.

请返回一个能打开保险箱的最短字符串。

原文：

There is a safe protected by a password. The password is a sequence of n digits where each digit can be in the range [0, k - 1].

The safe has a peculiar way of checking the password. When you enter in a sequence, it checks the most recent n digits that were entered each time you type a digit.

For example, the correct password is "345" and you enter in "012345":
- After typing 0, the most recent 3 digits is "0", which is incorrect.
- After typing 1, the most recent 3 digits is "01", which is incorrect.
- After typing 2, the most recent 3 digits is "012", which is incorrect.
- After typing 3, the most recent 3 digits is "123", which is incorrect.
- After typing 4, the most recent 3 digits is "234", which is incorrect.
- After typing 5, the most recent 3 digits is "345", which is correct and the safe unlocks.

Return any string of minimum length that will unlock the safe at some point of entering it.

示例 1

Input: n = 1, k = 2

Output: “10”

Explanation: The password is a single digit, so enter each digit. “01” would also unlock the safe.

示例 2

Input: n = 2, k = 2
Output: “01100”
Explanation: For each possible password:

“00” is typed in starting from the 4th digit.
“01” is typed in starting from the 1st digit.
“10” is typed in starting from the 3rd digit.
“11” is typed in starting from the 2nd digit.
Thus “01100” will unlock the safe. “01100”, “10011”, and “11001” would also unlock the safe.

提示

1 <= n <= 4
1 <= k <= 10
1 <= kⁿ <= 4096

算法一：贪心

思路

题意转换：「求出一个最短的字符串，使其包含从 0∼kⁿ（k进制）中的所有数字」，即将所有的 n−1 位数作为节点。每个节点有 k 条边，节点上添加数字 0∼ k−1 视为一条边。

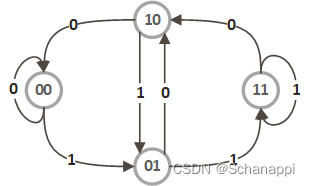
举例说明，如 n=3, k=2（三位二进制数），其节点（二位二进制数）为 “00”，“01”，“10”，“11” ，每个节点有 2 条边，节点上添加数字 0∼1 可转化到自身或另一个节点，如下图所示。
如果我们从任一节点出发，能够找出一条路径，经过图中的所有边且只经过一次，然后把边上的数字写入字符串（还需加入起始节点的数字），那么这个字符串显然符合要求，而且找不出比它更短的字符串了。
从任一节点开始，从 0∼k−1 遍历，只要有可用的路就走，直到无法继续为止。 当我们无路可走时，一定是在起始点，并且起始点的所有边都已经过。这是因为所有节点的入度和出度均为 k 。如果我们不在起始点，那 “只要有进去的路，就一定还有至少一条出去的路”。
再看之前出现的无路可走的情况，我们发现，起始点回的太早了。从贪心的角度来想，如果可以 尽可能晚返回起始点，就能遍历更多的边。
如果实现这个算法呢？

我们选择 “00” 作为起始点。每次要选择添加的数字时，从大数字开始（即从 k−1 遍历到 0），这样可以尽可能晚地回到起始点。
如何得到下一个节点的下标 ？

即解释 idx = (idx * k + edge) % nodeNum;

对于一个 k 进制数，如果当前节点对应的数为 a1 a2 ⋯ an−1，那么它的第 x 条出边就连向数 a2 ⋯ an−1 x 对应的节点（下一个节点），那么下一个节点如何表示呢? （这里节点和下标是等价的）

想象一下 10 进制，如何 9846 – x = 9 --> 8469
显然就是 8469 = (9846 * 10 + 9) % 10000
如果是 k 进制，那么就是 a2⋯an−1x = (a1a2⋯an−1 * k + x) % nodeNum

收获

这道题涉及到 欧拉路径 和 Hierholzer 算法，具体介绍见参考资料3 。解法一倒是没怎么涉及这些知识，用了贪心的思想，原理挺好理解的，但是代码难懂，尤其是下一个节点的下标计算，我看了很多解释才明白，解法一的正确性证明见参考资料 1。

算法情况

时间复杂度：O（kⁿ）
空间复杂度：O（kⁿ）

代码

class Solution {
public:
	string crackSafe(int n, int k) {
		//k的n-1次方个节点，每个节点有k条出边，所以图有k的n次方条边。
		int edgesNum = pow(k, n), nodeNum = pow(k, n - 1);
		//数组node是用来存储每个节点的出边，出边用索引表示，最大索引是k-1
		vector<int> node(nodeNum, k - 1);
		//这里多出来的n-1，其实是因为要初始化第一个节点"00..0"
		string s(edgesNum + (n - 1), '0');
        //idx表示节点索引
		for (int i = n - 1, idx = 0; i < s.size(); ++i) {
			int edge = node[idx];
			s[i] = edge + '0';
			//将对应的边出栈
			node[idx]--;
			//一共k^(n-1)个节点，可以看作n-2位的k进制数能表示的数，
			//即最小为0，最大为k^(n-1) - 1 (想象一下10进制，比如10^2，就好理解了)
			//如果当前节点对应的数为a1,a2,⋯,an−1，那么它的第x条出边就连向数 a2,⋯,an−1,x对应的节点
			//那么计算通向的下一个节点，需要先对当前的数进行左移操作（即在数值右端补0）
			//所以先 * k, 然后加上出边x，最后再通过 % 来抹去高位的a1。
			idx = (idx * k + edge) % nodeNum;
		}
		return s;
	}
};