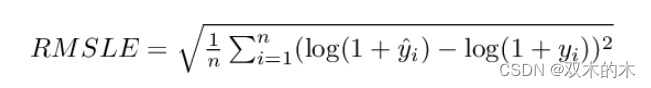毕业答辩PPT模板涵盖多种风格,包括母版的设计及主题色的设计
- 前言
- 一两个页面的展示
- 研究内容主题概述
- 主题内容一:主要面向三点研究内容
- 主题内容二:主要面向两点研究内容
- 主题内容三:主要面向包含应用开发的研究
前言
之前做了有关开题,中期答辩的PPT模板,最近又学到了一些PPT的技能😂。刚好也在做毕设答辩的PPT,所以打算抽离出来作为PPT模板。与之前不同的是,这一次添加了一些关于母版的设计及主题色的设计,方便同学的更改与设计。而且这一次包含多种颜色的主题!以及不同的汇报风格,可以方便研究内容多或少的同学进行选择。而且可以方便更多学校的同学做选择,可以将学校的logo替换掉,非常方便。
🖊 一些打杂打发时间的无聊时刻😪
ps:一些PPT计划在进行中,后面再来放资源了😂…
原创设计,未经同意,请勿转载,侵权必究
希望下面我的研究排版设计对你们也有所帮助,哈哈哈哈
一两个页面的展示
这里因为笔者我还没有放资源,所以先放一两个界面展示吧,其他风格样式其实也可以参考我现有的PPT风格,因为毕竟是毕业答辩,所以是偏学术风。
之前的PPT答辩模板:
- 【PPT模板合集】关于自制内容的PPT模板合集,包括原创的PPT及改良内容的PPT,适合科研/比赛/工作
- 华工各种毕设答辩PPT模板(包括开题,中期和最终答辩)
- 华工考研复试模板
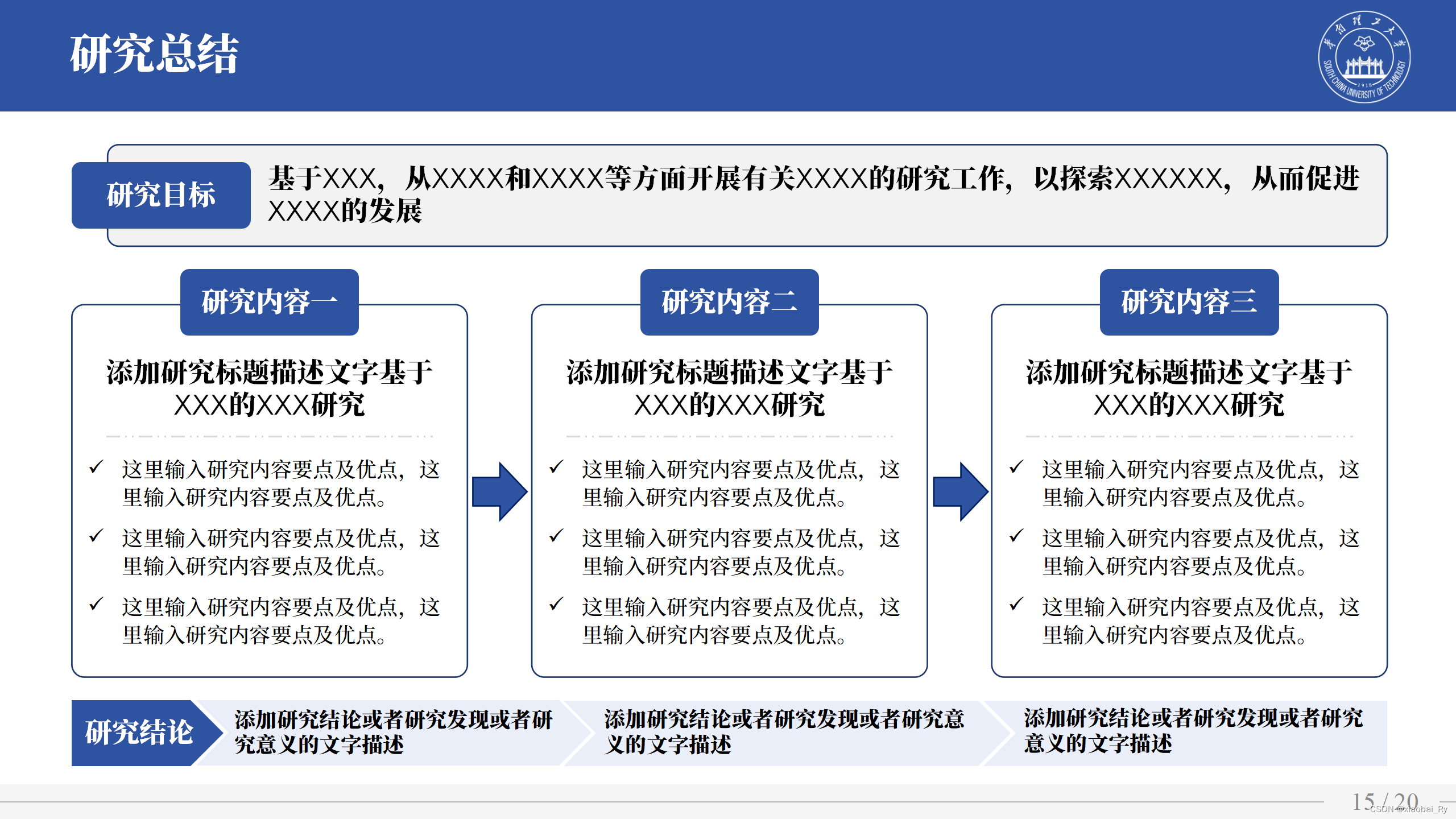
研究内容主题概述
下面主要是笔者面向不同研究内容情况做的PPT概述。主要是按照研究内容(目录)来分类,每个主题内容下,包括多种颜色主题!
主题内容一:主要面向三点研究内容
待更新
主题内容二:主要面向两点研究内容
待更新
主题内容三:主要面向包含应用开发的研究
待更新