搭建一个简单的网络结构（Pytorch实现二分类）

搭建一个神经网络并进行训练的话，大致需要分为三步：

第一步是数据的处理，将数据整理成输入网络结构中合适的格式
第二步是网络的搭建，包括每层网络的结构和前向传播
第三步是网络的训练，包括损失计算，优化器选择，梯度清零，反向传播，梯度优化等

这里我们以简单的二分类来进行一个简单的网络搭建：

一、数据处理

首先来生成含200个样本的数据

#生成200个点的数据集，返回的结果是一个包含两个元素的元组 (X, y),X是点，y是x的分类
X, y =  sklearn.datasets.make_moons(200, noise = 0.2)

并绘制出样本的散点图如下图所示：

save_path = "/data/wangweicheng/ModelLearning/SimpleNetWork"
plt.scatter(X[:,0],X[:,1],s=40,c=y,cmap=plt.cm.Spectral)
plt.savefig(f'{save_path}/dataset.png')   #保存生成的图片

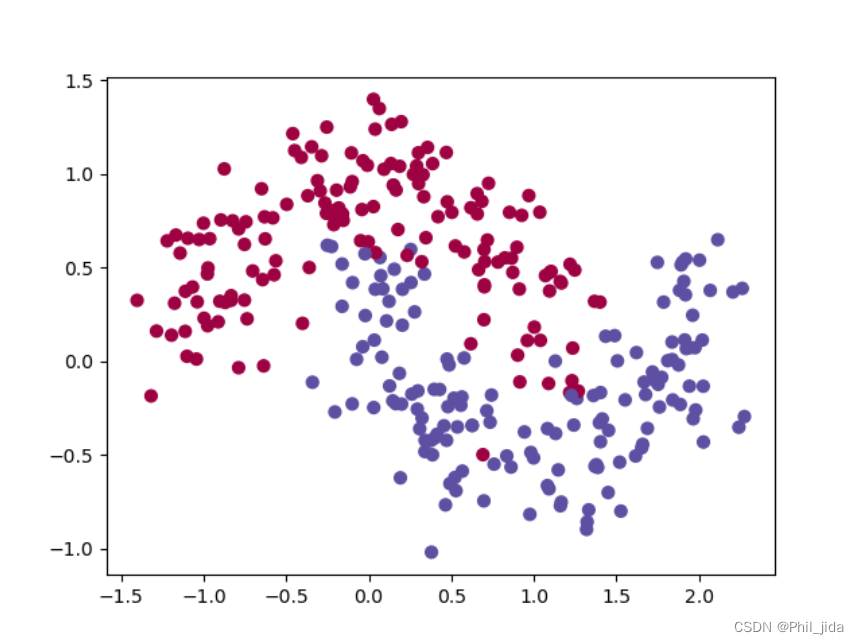
在这里插入图片描述

**可以看到我们生成了两类数据，分别用 0 和 1 来表示。**我们接下来将要在这个样本数据上构造一个分类器，采用的是一个很简单的全连接网络，网络结构如下：

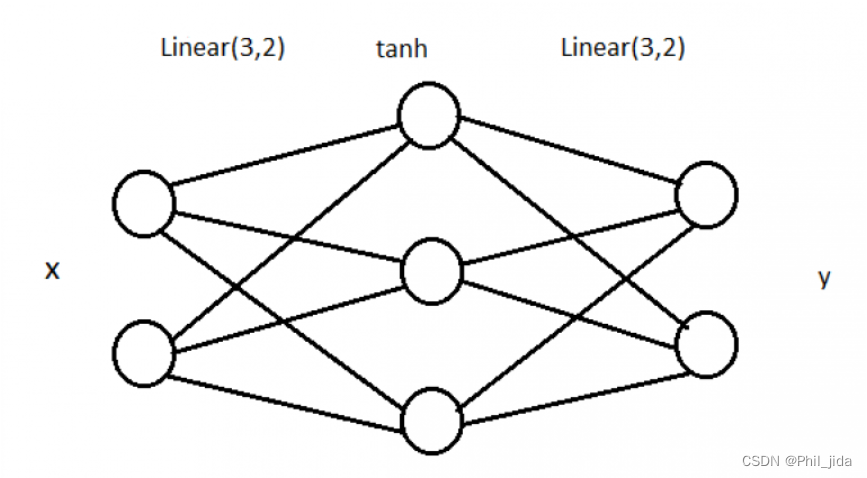
在这里插入图片描述

这个网**络包含一个输入层，一个中间层，一个输出层。**中间层包含 3 个神经元，使用的激活函数是 tanh。当然，中间层的神经元越多，分类效果一般越好，但这个 3 层的网络对于我们的样本数据已经足够用了。我们来算一下参数数量：上图中一共有 6 6 = 12 条线，就是 12 个权重，加上 3 2 = 5 个 bias，一共 17 个参数需要训练。

最后我们将样本数据从 numpy 转成 tensor：，后面我们就可以进行网络的搭建了

# 将 NumPy 数组转换为 PyTorch 张量，并指定张量的数据类型
X = torch.from_numpy(X).type(torch.FloatTensor)
y = torch.from_numpy(y).type(torch.LongTensor)

二、网络搭建

# 搭建网络
class BinaryClassifier(nn.Module):
    #初始化，参数分别是初始化信息，特征数，隐藏单元数，输出单元数
    def __init__(self,n_feature,n_hidden,n_output):
        super(BinaryClassifier, self).__init__()
        #输入层到隐藏层的全连接
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        #隐藏层到输出层的全连接
        self.output = torch.nn.Linear(n_hidden, n_output)

    #前向传播，把各个模块连接起来，就形成了一个网络结构
    def forward(self, x):
        x = self.hidden(x)  
        x = torch.tanh(x)   #激活函数
        x = self.output(x)
        return x
    
      
    def predict(self,x):
        #训练好之后，重新将x输入到网络中，进行测试
        #softmax得到0到1的一个值
        pred = F.softmax(self.forward(x),dim=1)
        ans = []
        #对不同点分别进行判断，如果第一个位置的数值大于第二个位置，就返回0，反之返回1
        for t in pred:
            if t[0]>t[1]:
                ans.append(0)
            else:
                ans.append(1)
        return torch.tensor(ans)

三、网络训练

选择损失函数CrossEntropyLoss，以及梯度优化器 Adam：

#初始化模型
model = BinaryClassifier(2, 3, 2)
#定义损失函数，用于衡量模型预测结果与真实标签之间的差异。
loss_criterion = nn.CrossEntropyLoss()
#定义优化器，优化器（optimizer）用于更新模型的参数，以最小化损失函数并提高模型的性能
# model.parameters() 表示要优化的模型参数，lr=0.01 表示学习率（learning rate）为 0.01，即每次参数更新的步长。
optimizer = torch.optim.Adam(model.parameters(), lr = 0.01)

进行迭代，获取当前loss，清除上一次的梯度，进行梯度下降和反向传播，更新参数：

#训练的次数
epochs = 10000
#存储loss
losses = []

for i in range(epochs):
    #得到预测值
    y_pred = model.forward(X)
    #计算当前的损失
    loss = loss_criterion(y_pred, y)
    #添加当前的损失到losses中
    losses.append(loss.item())
    #清除之前的梯度
    optimizer.zero_grad()
    #反向传播更新参数
    loss.backward()
    #梯度优化
    optimizer.step()
    if(i % 500 == 0):
        print('loss: {:.4f}'.format(loss.item()))

查看训练准确率：

print(accuracy_score(model.predict(X),y))

结果可视化：

def predict(x):
    x = torch.from_numpy(x).type(torch.FloatTensor)
    ans = model.predict(x)
    return ans.numpy()
    
# 画出边框
def plot_decision_boundary(pred_func,X,y):
    # 找到x，y的最大和最小值，并填充一些边框
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01
    # 生成一个网格
    xx,yy=np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # 将两个展平后的一维数组 xx.ravel() 和 yy.ravel() 按列连接起来，生成一个二维数组，然后对这个点进行预测
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    # 将预测结果 Z 重塑为与点网格 xx 相同的形状
    Z = Z.reshape(xx.shape)
    # 画出图像，绘制等高线图的代码
    plt.contourf(xx, yy, Z, cmap=plt.cm.YlGnBu)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.binary)
    plt.savefig(f'{save_path}/dataout.png')
    
    
plot_decision_boundary(lambda x : predict(x) ,X.numpy(), y.numpy())

输出结果：

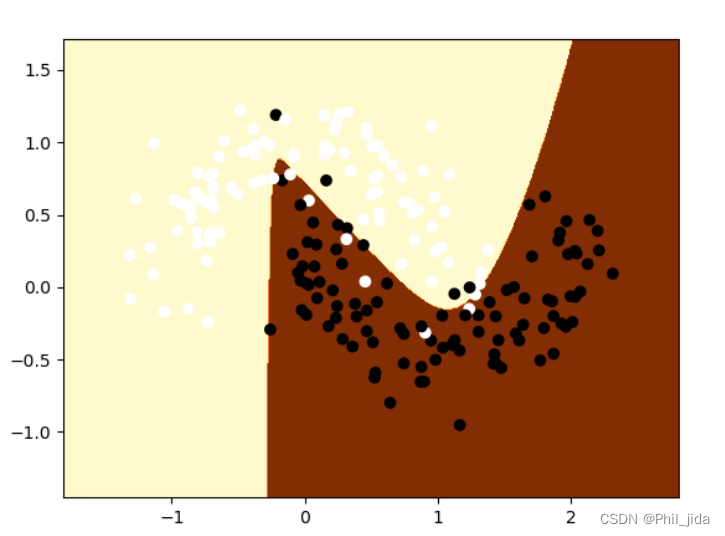
在这里插入图片描述

结果还是不错的！

完整代码：GitHub

#引入必要的包
#数据处理的包
import matplotlib.pyplot as plt
from sklearn.cluster import SpectralClustering
import sklearn.datasets
import numpy as np
#搭建网络的包
import torch
import torch.nn as nn
import torch.nn.functional as F
#统计分数
from sklearn.metrics import accuracy_score

#生成200个点的数据集，返回的结果是一个包含两个元素的元组 (X, y),X是点，y是x的分类
X, y =  sklearn.datasets.make_moons(200, noise = 0.2)

save_path = "/data/wangweicheng/ModelLearning/SimpleNetWork"
plt.scatter(X[:,0],X[:,1],s=40,c=y,cmap=plt.cm.Spectral)
plt.savefig(f'{save_path}/dataset.png')     #保存生成的图片

# 将 NumPy 数组转换为 PyTorch 张量，并指定张量的数据类型
X = torch.from_numpy(X).type(torch.FloatTensor)
y = torch.from_numpy(y).type(torch.LongTensor)


# 搭建网络
class BinaryClassifier(nn.Module):
    #初始化，参数分别是初始化信息，特征数，隐藏单元数，输出单元数
    def __init__(self,n_feature,n_hidden,n_output):
        super(BinaryClassifier, self).__init__()
        #输入层到隐藏层的全连接
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        #隐藏层到输出层的全连接
        self.output = torch.nn.Linear(n_hidden, n_output)

    #前向传播，把各个模块连接起来，就形成了一个网络结构
    def forward(self, x):
        x = self.hidden(x)  
        x = torch.tanh(x)   #激活函数
        x = self.output(x)
        return x
    
      
    def predict(self,x):
        #训练好之后，重新将x输入到网络中，进行测试
        #softmax得到0到1的一个值
        pred = F.softmax(self.forward(x),dim=1)
        ans = []
        #对不同点分别进行判断，如果第一个位置的数值大于第二个位置，就返回0，反之返回1
        for t in pred:
            if t[0]>t[1]:
                ans.append(0)
            else:
                ans.append(1)
        return torch.tensor(ans)


#初始化模型
model = BinaryClassifier(2, 5, 2)
#定义损失函数，用于衡量模型预测结果与真实标签之间的差异。
loss_criterion = nn.CrossEntropyLoss()
#定义优化器，优化器（optimizer）用于更新模型的参数，以最小化损失函数并提高模型的性能
# model.parameters() 表示要优化的模型参数，lr=0.01 表示学习率（learning rate）为 0.01，即每次参数更新的步长。
optimizer = torch.optim.Adam(model.parameters(), lr = 0.01)

#训练的次数
epochs = 10000
#存储loss
losses = []

for i in range(epochs):
    #得到预测值
    y_pred = model.forward(X)
    #计算当前的损失
    loss = loss_criterion(y_pred, y)
    #添加当前的损失到losses中
    losses.append(loss.item())
    #清除之前的梯度
    optimizer.zero_grad()
    #反向传播更新参数
    loss.backward()
    #梯度优化
    optimizer.step()
    if(i % 500 == 0):
        print('loss: {:.4f}'.format(loss.item()))


#进行预测
print(accuracy_score(model.predict(X),y))

def predict(x):
    x = torch.from_numpy(x).type(torch.FloatTensor)
    ans = model.predict(x)
    return ans.numpy()
    
# 画出边框
def plot_decision_boundary(pred_func,X,y):
    # 找到x，y的最大和最小值，并填充一些边框
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01
    # 生成一个网格
    xx,yy=np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # 将两个展平后的一维数组 xx.ravel() 和 yy.ravel() 按列连接起来，生成一个二维数组，然后对这个点进行预测
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    # 将预测结果 Z 重塑为与点网格 xx 相同的形状
    Z = Z.reshape(xx.shape)
    # 画出图像，绘制等高线图的代码
    plt.contourf(xx, yy, Z, cmap=plt.cm.YlOrBr)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.binary)
    plt.savefig(f'{save_path}/dataout.png')
    
    
plot_decision_boundary(lambda x : predict(x) ,X.numpy(), y.numpy())