数据结构：图的最短路径

一、最短路径的基本概念

二、无权图单源最短路径

三、Dijkstra算法（正权图单源）

3.1、算法的基本步骤

3.2、算法的实现

3.3、习题思考

3.3.1、网络延迟时间

四、A*算法（正权图单源单目标点）

4.1、算法的基本概念

4.2、算法的重要证明

五、Floyd算法（带权每对顶点间的最短路）

5.1、算法的基本原理

5.2、算法的实现

5.3、扩展

六、Bellman-Ford算法（负权图单源最短路径问题）

6.1、算法的基本原理

6.2、算法的实现

七、SPFA（贝尔曼福特队列优化）

7.1、算法的基本思想

7.2、算法的实现

本篇所有证明都是博主自己想的，如有疑问，扔给GPT，他会帮你解答。

一、最短路径的基本概念

无权图：路径包含的边的条数。
带权图：路径包含的各边权值之和。
长度最小的路径称为最短路径，最短路径的长度也称为最短距离。

二、无权图单源最短路径

无权图单源最短路径使用BFS求出，时间复杂度为O(n+e)。该算法可以求出单源到所有顶点的最短路，并且可以通过静态链表的方式存储各顶点的最短路径信息。

在BFS访问的过程中，当访问某个顶点时，就确定了该点与源点的最短距离。

#include<bits/stdc++.h>
using namespace std;
#define n 10
struct Edge{
    int VerName;
    Edge * next;
};
struct Vertex{
    int VerName;
    Edge * edge=nullptr;
};
vector<int> path(n);
Vertex Head[n];
vector<int> dist(n,0x3f3f3f3f);
void BFS(Vertex * Head,int s){
    dist[s]=0;path[s]=-1;
    queue<int> q;
    q.push(s);
    while(!q.empty()) {
        int pre=q.front();q.pop();
        for(Edge * edge=Head[pre].edge;edge!=nullptr;edge=edge->next) {
            int k=edge->VerName;
            if(dist[k]==0x3f3f3f3f) {//未被访问过
                dist[k]=dist[pre]+1;
                q.push(k);
                path[k]=pre;//记录该路径的前驱
            }
        }
    }
    return;
}
int main(void) {return 0;}

三、Dijkstra算法（正权图单源）

虽然在关键路径中，我们使用过拓扑排序+动态规划求最长路径，时间复杂度是O(n+e)。但是这是在图存在拓扑排序时才能使用的。一般情况下的图更加复杂。一般情况下的正权图，可以使用迪杰斯特拉算法求出最短路径。迪杰斯特拉不能求带有负权图的最短路径。

Dijkstra算法可以求出单源点到所有点的最短路径。该算法使用优先队列可以优化成O(nlogn+e)。

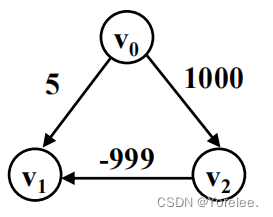
Dijkstra算法不能求负权图的原因是，即使当前在优先队列中选定了当前距离源点最短的一个点，此时确定它的最短路径，但是由于负权边的存在，可能使得未来，它到源点的最短距离更短。比如求v0到各点的最短路，下图中的v1会比v2先确定，且认为v1的最短路就是5，实际上应该是先选择v2，求得v1最短路是-1。如果仅仅存在正权，路径的权值只能增加不能减少，当前最小就是最小（贪心的局部最优），因此不会出现这样的情况。

3.1、算法的基本步骤

①将图中的所有顶点分成两个集合，一个是集合S，一个是集合V-S，S中的顶点表示已经确定最短路的顶点，V-S中表示尚未确定最短路的顶点。

②在初始时S为空集，将源点压入优先队列，执行③

③在V-S中选择离源点最近的顶点（包括源点自身），将该顶点放入S，表示该顶点已经求出最短路径，执行④

④遍历该顶点的所有边，更新其他顶点的最短路径，重复③，直至所有顶点都已经求出最短路径。

其主要思想是贪心。该算法实现时遍历所有顶点一次，遍历所有边一次，对于每一个顶点的所有边访问的顶点只要不在S中都压入优先队列中（延迟出栈，不修改队列中的元素，也可以直接自定义实现修改队列中的元素），可能重复压栈，因此时间复杂度为O(nloge+e)。由于e<=n^2 loge<=2logn，取最大阶，因此时间复杂度为O(nlogn+e)。

正确性证明：证明在S中的顶点的最短路一定被求出，在V-S中新选择的顶点其最短路一定已经被求出。

数学归纳法：令S中的元素个数为n

①当n=0时，选择源点，源点到源点必然是最短路。

②当n=1时，即源点更新最短路，在V-S中选择一步到源点的最短边对应的顶点v，也一定是v的最短路，因为从源点走其他一步的长度都比源点到v的路径更长，因此直接走到v必然是最短的，将其加入到S中，此时S中的元素都已经被求出最短路。

③当n=k-1时(k>=1)，反证法：假设在V-S当前到源点的最短的距离顶点为v，假如目前该最短距离还不是源点到v的最短路，则必然有一条源点到v的路径经过一点u，使得源点到v的最短路距离更短（且u不在S中，不然u就已经更新过v了，就不存在这个u的说法了），由于最短路的性质，此时源点到u的最短路会更短，且u不在S中，所以应该选择的是u而不是v，因此与选择v矛盾，则目前该最短距离是v到源点的最短路，将其加入到S中，此时S中的元素都已经被求出最短路，证毕。

3.2、算法的实现

这里采用STL的优先队列的方法，优先队列采用延迟出栈，出栈的顶点若不在S中，则选择它，如果出栈的顶点在S中，则忽略该顶点，直至找到真正不在S中的顶点，多个副本在优先队列中是没问题的，因为多个副本距离最短的优先出队。出队防止队列为空！

这里直接通过距离来判断是否在S中：同样的距离仍然会被更新，但是不影响。

int n=100;
vector<int> dist(n,0x3f3f3f3f);
vector<int> path(n);
void Dijkstra(Vertex * Head,int s){
    priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;//默认是大根堆，定义小根堆! {dist,k} 直接使用pair的比对函数，先比较dist，dist小者优先
    q.push({0,s});
    dist[s]=0;path[s]=-1;
    while(!q.empty()){//优先队列不为空继续遍历，如果已经遍历了所有顶点，循环内部也会解决该问题
        int pre=q.top().second;
        int dis=q.top().first;q.pop();
        if(dist[pre]<dis) continue;//优先队列中弹出的pre的最小值，应当是当前pre存储的最小值，才算是最小的，不是最小的出队。不能保证每个点只更新一次，但这样的多次更新对结果没影响
        for(Edge * edge=Head[pre].edge;edge!=nullptr;edge=edge->next) {
            int k=edge->VerName;
            if(dist[k]<dist[pre]+edge->cost){//小时更新，等于时也不更新了。
                path[k]=pre;//更新前驱
                q.push({dist[k],k});//只有被更新了才导入，没被更新不是最优解就不导了
                
            }
        }
    }
    return;
}

使用vector实现的，并使用“集合”的思想：

        vector<int> S(n,0);
        while(!q.empty()){
            int pre=q.top().second;q.pop();
            if(S[pre]==1) continue;//pre在S中，即pre已经更新过则继续
            S[pre]=1;//标记pre放入S并更新，保证每个点只更新一次了
            for(auto i : Head[pre]) {
                int k=i.first;
                if(dist[pre]+i.second<dist[k]){//只有距离更短才放入，当然随着更新，可能同一个点多次放入，但是我们只在优先队列中选择一次，所以之后用S[pre]可以判断。
                    dist[k]=dist[pre]+i.second;
                    q.push({dist[k],k});
                }
            }
        }

3.3、习题思考

3.3.1、网络延迟时间

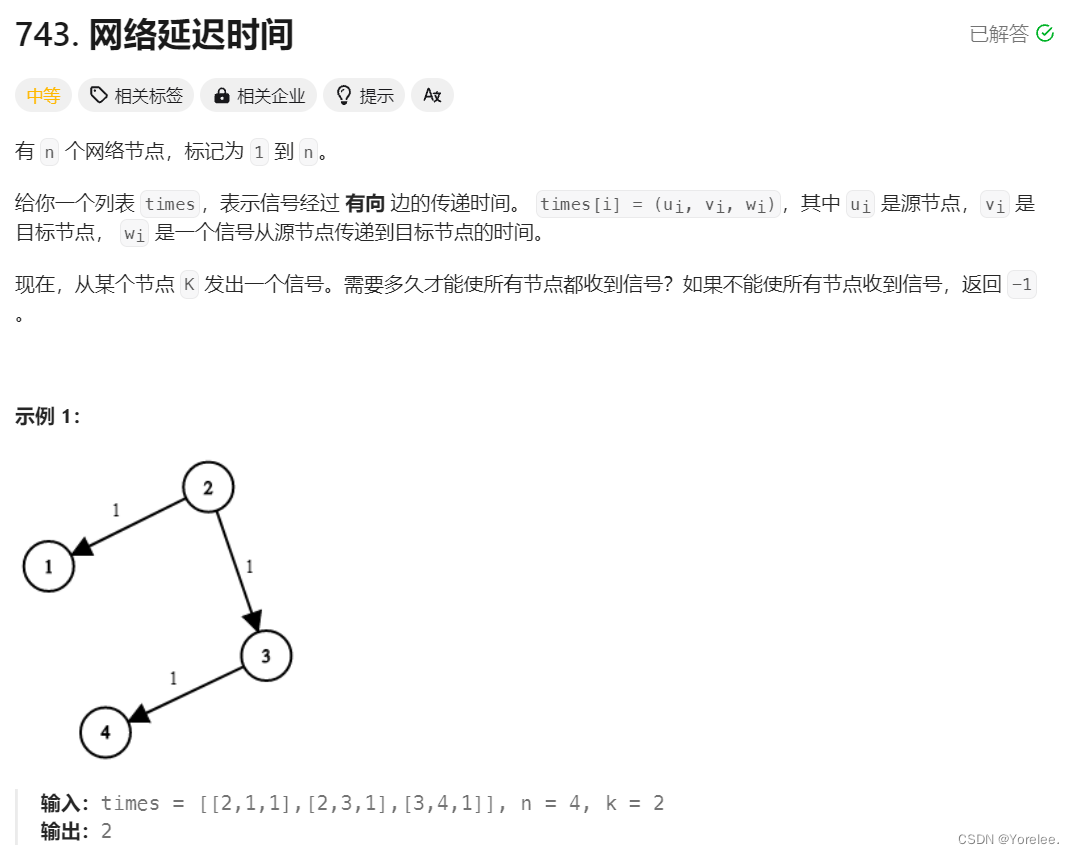
实际上由于STL的引入，存储边并不需要使用邻接表了，使用vector就能解决存储边的问题！以后我们都用vector存储边。

class Solution {
public:
    const int INF=0x3f3f3f3f;
    int Dijkstra(vector<vector<int>>& times, int n, int s) {
        vector<vector<pair<int,int> > > Head(n);
        for(auto &i:times){
            Head[i[0]-1].emplace_back(i[1]-1,i[2]);
        }
        vector<int> dist(n,0x3f3f3f3f);
        priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
        q.push({0,s});
        dist[s]=0;
        while(!q.empty()){
            int pre=q.top().second;
            int dis=q.top().first;q.pop();
            if(dist[pre]<dis) continue;//
            for(auto i : Head[pre]) {
                int k=i.first;
                if(dist[pre]+i.second<dist[k]){
                    dist[k]=dist[pre]+i.second;
                    q.push({dist[k],k});//只有被更新了才导入，没被更新不是最优解就不导了
                }
            }
        }
        int max=-1;
        for(auto i:dist) if(max<i) max=i;
        if(max!=INF) return max;
        return -1;
    }
        int networkDelayTime(vector<vector<int>>& times, int n, int k) {
            return Dijkstra(times,n,k-1);
        }
};

**四、A*算法（正权图单源单目标点）**

4.1、算法的基本概念

【路径规划】全局路径规划算法——A*算法（含python实现 | c++实现）

在游戏中，如《新倩女幽魂》里的自动寻路功能，通常采用路径规划算法来计算从当前位置到目标位置的最佳路径。这种路径规划可能会涉及到各种算法，如A*（A-Star）、Dijkstra等，这些算法在寻找最短路径的同时，也会考虑其他因素，如路径上的障碍、地形的不同代价以及可能的动态变化等。
A*算法是一种启发式搜索，它每次选择估价函数最小的顶点进行下一步移动。
A*算法的执行步骤和Dijkstra算法很相似，区别就是A*算法每次选择的不是没被选择过的里面距离源点最短的顶点更新，而是选择没被选择过的里面估价函数最低的顶点更新。
估价函数f(v) 包含了dijkstra里面距离源点的最短路径g(v)，还多出来了h(v)。并且我们更新的最短路实际上也是更新的g(v)，只是在选择更新时选择了f(v)而已，选择f(v)可以让算法更快抵达目标点。

4.2、算法的重要证明

当保证h(v)<=h*(v)时，我们根据之前的阐述可以发现，最短路的顶点是可能被选到的，因为h(v)==h*(v)时，最短路径上的顶点f(v)总是最小的，当h(v)不超过实际代价时，最短路径上的顶点f(v)也大概率会比其他顶点小，因此会优先被更新。并且对于一些顶点到源点的距离g(v)就可能已经超过了最短路径上的f(v)，因此不会再被更新。
证明启发函数小时能找到最短路：A* 算法的一个核心停止条件是当目标节点被移动到关闭列表（已经被更新过）时，此时算法认为已经找到了一条路径，并且基于启发式函数的设定，认为这是最优路径。如果h(v)>h*(v)，那么最优路径的顶点可能在优先队列中靠后，导致更新不及时，最终到达终点，找到近似解，当然也可能找到最优解。而如果h(v)<=h*(v)，则在终点更新扩展时，终点的估价函数等于f0，而最短路径上的估价函数等于f(v)=g(v)+h(v)<=g(v)+h*(v)<=f0，而若终点未被最短路径上的顶点更新，那么其f必然是大于f0的（因为g(v)更大，h(v)=0），因此最短路径上的顶点会比终点先扩展，g(v)是唯一确定的，扩展后终点的g(v)也会被确定为最短。这意味着，对于最短路径上的任一节点 v，f(v)≤f0，确保了在目标节点的 f0 值被确定之前，最短路径上的所有节点都已被考虑。这是因为 A* 算法总是优先扩展 f 值最小的节点。

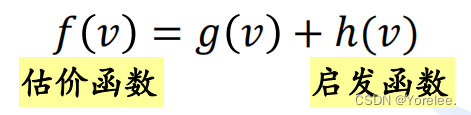
解释：

五、Floyd算法（带权每对顶点间的最短路）

带权每对顶点间的最短路：

①如果全是正权，可以让每个顶点都做一次源点，执行n次Dijkstra算法，时间复杂度为O(n²logn)

②带有负权，也可以使用Floyd算法，时间复杂度为O(n³)

5.1、算法的基本原理

        Floyd算法实际上是一个动态规划算法，它定义dp[k][i][j]，表示能经过顶点0~k时，i到j的最短路。

        状态转移方程：dp[k][i][j]=min(dp[k-1][i][j],dp[k-1][i][k]+dp[k-1][k][j])，即经过顶点0~k时，i到j的最短路等于 {经过顶点0~k-1时，i到j的最短路，可以经过顶点0~k-1时，i先经过k，再从k到j的距离}的最小值。

        降维优化，由于只用到之前的距离，因此可以直接将三维数组改写成二维dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])。//我们不需要担心i==k||j==k时，更新它是会影响之后的更新情况，不用担心，因为k能经过k 和k能经过0~k-1是没区别的。

         不允许存在负环（环上所有边的权值和为负数，理论上不存在最短路，因为可以无限小，Floyd此时求不出最短路）。Floyd算法可以判负环，初始时D[i][i]=0，算法执行过程中若D[i][i]<0，表示顶点i到自己的最短距离为负值，即存在负环。（可以这样考虑为什么不允许存在负环，初始化时，你将dp[i][i]初始化为0，表示自己到自己应该是0距离，而实际上存在负环，可以是负无穷，因此即使算法没逻辑问题，但是初始化就导致算法结果出现问题）

5.2、算法的实现

int A[n][n];
vector<vector<int> >dp(n,vector<int>(n,0));
vector<vector<int> >path(n,vector<int>(n,0));
void Floyd(int n){
    for(int i=0;i<n;++i)
        for(int j=0;j<n;++j){
            dp[i][j]=A[i][j];
            if(i!=j)
                path[i][j]=i;//表示i到j的最短路 j 的前驱
            else path[i][j]=-1;
        }
    for(int k=0;k<n;++k)
        for(int i=0;i<n;++i)
            for(int j=0;j<n;++j)
                if(dp[i][j]>dp[i][k]+dp[k][j]){
                    dp[i][j]=dp[i][k]+dp[k][j];
                    path[i][j]=path[k][j];//i到j的最短路前驱变成了k到j的最短路前驱。
                }
    return;
}

5.3、扩展

不经过 v1,v2,v3,v4··的最短路（不存在v1,v2,v3,v4··为中间顶点时），我们直接让k不能等于它们即可。

    for(int k=0;k<n;++k)
        if(k!=v1&&k!=v2&&k!=v3&&k!=v4)//使得k不能作为中间结点~
        for(int i=0;i<n;++i)
            for(int j=0;j<n;++j)
                if(dp[i][j]>dp[i][k]+dp[k][j]){
                    dp[i][j]=dp[i][k]+dp[k][j];
                    path[i][j]=path[k][j];//i到j的最短路前驱变成了k到j的最短路前驱。
                }

六、Bellman-Ford算法（负权图单源最短路径问题）

6.1、算法的基本原理

先看一下是什么：

再来说说为什么：

我们可以将源点到所有顶点的所有可能路径展开（类似一个散射图），不管重不重复出现，将所有可能的路径都向外展开就行。这样，我们将所有的可能路径都分开了，每一条单独而不影响！

我们再来看算法，当算法第1次迭代时，必定只有离原点只有一条边的顶点的距离被更新，第2次迭代时才可以更新离源点有两条边的顶点，依次类推。那么，我们是如何找到最短路的？对于同一个顶点v，可能出现在我们刚刚展开的图中两条（或多条）路径中，我们来证明一下v最短路径那条路径（包含e条边）一定会在e次迭代后被成功更新，即第e次一定会迭代出v的最短路径长度。假设v的最短路径包含e条边，且前驱是u，根据最短路的性质，源点到u也应该是最短路，若不然，u的最短路在另外一条路径中的长度应该更长（至少包含e条边，因为本条路径对于u来说到源点一共e-1条边），因为u还未被更新为最短路，一旦被更新为最短路，则u的最短值不可能被更改，所以u如果在v的该路中不是最短路，则u应该会更长，这与v的前驱是u，且最短路包含e条边矛盾，因为u可以更短且包含更多的边，则v的前驱有u，则v也可以包含更多的边而不是e，与之前矛盾，所以u确实是v的最短路。证毕。

再来看看更容易的证明：

最优子结构的存在，对于v的最短路来说，源点到v之前的所有顶点都必然是自己的最短路，这样的话，v的最短路e条边，实际上迭代e次必然就出现了~（因为迭代e次相当于只能往外走e次，并且一旦被更新为最短路，则最短值不可能被更改）。

最优子结构是因为，源点到v的最短路经过x，那么源点到x也必然是最短路，因为v的最短路=<源点,u,x>+<x,,v)，如果<源点,u,x> 不是x的最短路，那么换一个最短的，v还能短，所以v最短必然x也最短~（）

6.2、算法的实现

不存储边：时间复杂度O(n²+ne)<=O(n³)，注意，虽然最坏也是n³，但是Floyd可以求两两之间的最短路～

vector<int> path(n,-1);
vector<int> dist(n,0x3f3f3f3f);
bool Bellman_Ford(vector<vector<pair<int,int> > > & g,int n,int s){
    dist[s]=0;
    for(int k=1;k<n;++k)//只需要迭代n-1次 就行~
        for(int i=0;i<g.size();++i)
            for(int j=0;j<g[i].size();++j)
                if(dist[i]+g[i][j].second<dist[j]){
                    dist[j]=dist[i]+g[i][j].second;
                    path[j]=i;
                }
    
    for(int i=0;i<g.size();++i)//检测负环
        for(int j=0;j<g[i].size();++j)
            if(dist[i]+g[i][j].second<dist[j]){//还能更新，存在负环！
                return false;
            }
    return true;
}

存储边：时间复杂度O(n+ne)<=O(n³)

vector<int> path(n,-1);
vector<int> dist(n,INT_MAX);
bool Bellman_Ford(vector<vector<pair<int,int> > > & g,int n,int s){
    vector<pair<int,pair<int,int> > > edge;
    for(int i=0;i<g.size();++i)
        for(auto &j:g[i])
            edge.push_back({i,j});
    dist[s]=0;
    for(int k=1;k<n;++k)//只需要迭代n-1次 就行~
        for(auto & i:edge)
            if(dist[i.first]+i.second.second<dist[i.second.first]){
                dist[i.second.first]=dist[i.first]+i.second.second;
                path[i.second.first]=i.first;
            }
    
    for(auto & i:edge)//检测负环
       if(dist[i.first]+i.second.second<dist[i.second.first]){
          return false;
       }
    return true;
}

七、SPFA（贝尔曼福特队列优化）

SPFA实际上是贝尔曼福特算法的队列优化版本。

SPFA存在卡时，如网格图可以将SPFA卡成O(ne)。

7.1、算法的基本思想

        SPFA和Bellman-Ford算法的区别在于，SPFA每次迭代并不遍历所有边，因为可能有些边的遍历是多余的，比如第k-1次遍历，没有更新dist[u]，且第k-1次遍历会遍历尝试更新u邻接的所有顶点的dist，则第k次遍历用上一次一样的dist[u]继续更新是没有意义的。

        因此我们使用的方法的核心思想仍然是迭代次数遍历边，但是我们只遍历这次迭代被更新顶点的边：我们使用一个队列保存需要用来更新的顶点，用该顶点更新其邻居，当其邻居的dist被更新了，则将其邻居入队，相当于下一次迭代我们只需要遍历这些被更新的邻居即可，由于队列是先进先出的，我们直接不断取出不断弹出直到队列为空即可。这里我们还可以优化一部分，就是如果在队列中的顶点就不需要继续入队，因为一个点v 更新其邻接顶点使用越接近最短距离的越好；可能在“本次迭代”更新的时候，压入了一个顶点u，然后之后的某一次这个顶点u还没出队，又更新了这个顶点u，这个顶点u如果在队列中我们就不需要压入了，原因是即使是不压入，u也确实被更新了，它仍然会带着这个被更新的值继续用最好的dist去更新。（这和dijkstra不一样， SPFA队列中是点不是值值在外部）



入队次数等于n说明个什么问题？

        由于SPFA相当于Bellman-Ford算法的优化，实际上也是一个迭代过程，如果我们保证每次迭代队列中的元素只入队一次的话。也就是说可以想象成队列中的元素是按迭代次序摆放的且分开的，下一次迭代的元素会在本次被压入队列中，因此近似地入队次数可以被认为是一个顶点的迭代次数。准确的说，入队次数是≤Bellman-ford的迭代次数的，因为第k次迭代更新的顶点的结果应该在k+1次迭代中使用并进行更新其邻接顶点，但是可能在第k次迭代被更新时，此时还没出队，即它也将进行第k次迭代，则它不会再被入队，因此也不会参与第k+1次迭代了，即第k+1次不会更新该顶点的邻居，所以入队次数少于等于实际的迭代次数的，如果此时入队次数达到了n则至少在Bellman-Ford算法中的迭代次数达到了n，负权环的存在可以使得更新产生无数次，入队次数也可以无数次。

        如果入队次数等于n说明一个顶点在不同的路径中存在着n个不同的位置，否则根据Bellman-Ford算法的思想，它不能被迭代n次！而不存在负环的图，n个顶点，任何一个顶点最多出现在一条路的n-1个不同的位置，因此如果有n个位置就说明存在负环，路径可以无限长。

7.2、算法的实现

bool SPFA(vector<vector<pair<int,int>>> &g,int n,int s){
    vector<int> path(n,-1);
    vector<int> times(n,0);//入队次数
    queue<int> q;
    vector<int> dist(n,INT_MAX);
    vector<int> Inqueue(n,0);
    dist[s]=0;
    q.push(s);times[s]+=1;
    while(!q.empty()){
        int u=q.front();q.pop();
        Inqueue[u]=0;
        for(auto &i:g[u]){
            int v=i.first;int weight=i.second;
            if(dist[u]+weight<dist[v]){
                dist[v]=dist[u]+weight;
                path[v]=u;
                if(Inqueue[v]==0){
                    Inqueue[v]=1;
                    q.push(v);
                    if(++times[v]==n) return false;//一次迭代只算一次入队哦
                }
            }
        }

    }
    return true;
}