损失函数

Dice Loss

Dice Loss 是一种用于图像分割的损失函数，其灵感来自于Dice 系数，是一种衡量两个样本相似度的方法。Dice 系数定义为：

Dice 系数 = 2 * TP / (2 * TP + FP + FN)

其中：

TP：预测为正且真实值为正的像素数量
FP：预测为正且真实值为负的像素数量
FN：预测为负且真实值为正的像素数量
Dice 系数的值域为 [0, 1]，值越大表示两个样本越相似。

Dice Loss 的定义为：
$$DiceLoss=1-Dice系数=1-2\ast TP/(2\ast TP+FP+FN)$$
Dice Loss 的特点：

能够克服类别不平衡问题：Dice Loss 直接使用预测和真实值之间的重叠面积来衡量相似度，因此能够有效克服类别不平衡问题。
梯度平滑：Dice Loss 的梯度是平滑的，这使得模型训练更加稳定。

Dice Loss 的应用：

图像分割：Dice Loss 是图像分割中常用的损失函数，特别适用于分割小目标或不规则目标。
医学图像分割：Dice Loss 在医学图像分割中也得到了广泛应用，例如，用于分割肿瘤、器官等。
Dice Loss 代码讲解
PyTorch 中的 Dice Loss 代码实现如下：

import torch

def dice_loss(pred, target):
    # 计算预测和真实值之间的重叠面积
    intersection = (pred * target).sum()
    # 计算预测和真实值的面积
    union = pred.sum() + target.sum()
    # 计算 Dice Loss
    dice_loss = 1 - (2 * intersection) / union
    return dice_loss

.
总结
Dice Loss 是一种用于图像分割的有效损失函数，能够克服类别不平衡问题，并且梯度平滑。其代码实现也比较简单，可以方便地应用于各种图像分割任务。

Lovasz-Softmax损失函数

Lovasz-Softmax损失函数的中文解释和代码解释

1. 简介
   Lovasz-Softmax损失函数是一种用于图像分割的损失函数，它可以有效地解决分割任务中常见的类别不平衡问题。该函数由Berman等人于2018年提出，并在论文《The Lovasz-Softmax loss: A tractable surrogate for the optimization of the intersection-over-union measure in neural networks》中进行了详细介绍。
2. 原理
   Lovasz-Softmax损失函数是基于Lovasz扩展构建的，该扩展可以将交并比（IoU）指标转换为一个可优化的损失函数。具体来说，Lovasz-Softmax损失函数可以表示为：

$$L(y,p)=-\sum _{i=1}^C\frac{1}{C}\left(1-\frac{I(y_i,p_i)}{U(y_i,p_i)}\right)$$

其中，
y 是真值标签，
p 是预测概率，
C 是类别数，
I(yi​,pi​) 是真值标签 yi​ 和预测概率 pi​ 的交集，
U(yi​,pi​) 是真值标签 yi​ 和预测概率 pi​ 的并集。

3. 优点
   Lovasz-Softmax损失函数具有以下优点：
   可以有效地解决类别不平衡问题，因为它不依赖于预测概率的绝对值，而是依赖于预测概率的相对大小。
   可以获得更准确的分割结果，因为它可以更好地处理边缘像素的分割问题。
   具有较强的鲁棒性，因为它可以抵抗噪声和干扰的影响。

4. 代码
   以下是Lovasz-Softmax损失函数的PyTorch代码实现：

def lovasz_softmax(probas, labels, classes='present'):
    """
    Multi-class Lovasz-Softmax loss as described in the paper
    "Lovasz-Softmax and Jaccard Hinge Loss for Semantic Segmentation"
    (https://arxiv.org/abs/1705.08797).

    Args:
        probas: (N, C, H, W) logits.
        labels: (N, H, W) labels.
        classes: 'present' or 'all'.

    Returns:
        Lovasz-Softmax loss.
    """
    if probas.dim() != 4:
        raise ValueError("probas must be 4D tensor")
    if labels.dim() != 3:
        raise ValueError("labels must be 3D tensor")
    if classes not in ['present', 'all']:
        raise ValueError("classes must be 'present' or 'all'")
    inter, union = _lovasz_softmax_inter_union(probas, labels, classes)
    loss = 1. - inter / union
    return loss.mean()

代码中的主要函数是 _lovasz_softmax_inter_union，该函数用于计算真值标签和预测概率之间的交集和并集。具体来说，该函数的代码如下：

def _lovasz_softmax_inter_union(probas, labels, classes):
    """
    计算真值标签和预测概率之间的交集和并集。

    参数：
        probas: (N, C, H, W) logits。
        labels: (N, H, W) 标签。
        classes: 'present' 或 'all'。

    返回值：
        inter, union.
    """

    if probas.dim() != 4:
        raise ValueError("probas必须是4D张量")
    if labels.dim() != 3:
        raise ValueError("labels必须是3D张量")
    if classes not in ['present', 'all']:
        raise ValueError("classes必须是'present'或'all'")

    if classes == 'present':
        # 计算每个类别的交集和并集
        inter, union = _lovasz_softmax_inter_union_present(probas, labels)
    elif classes == 'all':
        # 计算类别无关的交集和并集
        inter, union = _lovasz_softmax_inter_union_all(probas, labels)
    else:
        raise ValueError("classes必须是'present'或'all'")

    return inter, union

align

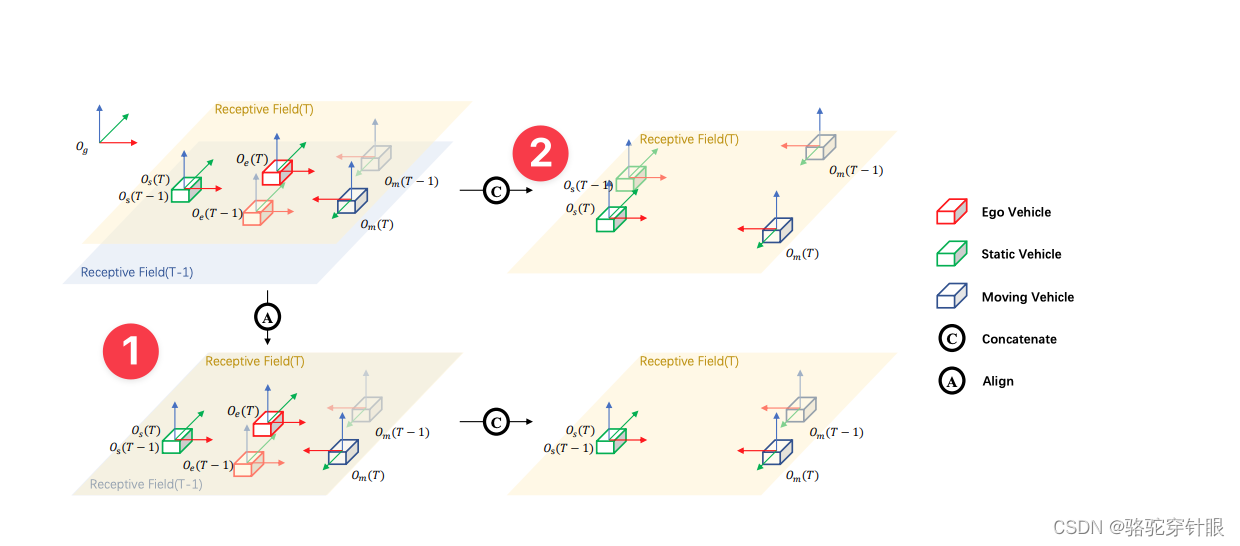
# 获取feat_prev的维度信息，其中_代表批量大小(batch size)，C是通道数，H是高度，W是宽度
_, C, H, W = feat_prev.shape

# 使用self.shift_feature方法对feat_prev进行特征对齐
# [sensor2keyegos_curr, sensor2keyegos_prev]用于指定当前帧和前一帧的传感器到关键帧的变换
# bda是变换或对齐参数
feat_prev = \
    self.shift_feature(feat_prev,
                        [sensor2keyegos_curr, sensor2keyegos_prev],
                        bda)

# 将对齐后的feat_prev重塑，并添加到特征列表bev_feat_list中
# 重塑后的特征尺寸为(1, (self.num_frame - 1) * C, H, W)，这里通过self.num_frame - 1计算得到的是
# 除当前帧外的帧数，乘以C得到总的通道数，H和W保持不变
bev_feat_list.append(feat_prev.view(1, (self.num_frame - 1) * C, H, W))

# 使用torch.cat将bev_feat_list中的所有特征在通道维度上进行拼接
# 得到的bev_feat是一个融合了多帧特征的张量
bev_feat = torch.cat(bev_feat_list, dim=1)

# 将融合后的特征张量bev_feat通过一个编码器(self.bev_encoder)进行处理
# 得到x，x是经过编码后的特征，可用于后续的任务，比如分类、回归等
x = self.bev_encoder(bev_feat)

调参

占用网络(Occupancy Networks)的调参策略至关重要。鉴于鸟瞰视图(BEV)架构的网络通常包含众多模块且相对庞大，其训练周期可能根据网络结构和数据规模的不同而变化，通常在1至5天之间。如果训练过程中出现长时间的损失(loss)停滞，将极大拖延实验进度，对科研活动或工作进度造成不利影响。

为了提高调参效率并优化训练过程，以下是一些实用的建议：

**确定批处理大小：**基于可用的数据集大小和资源限制，首先确定合适的批处理大小（batch size）。

优化器选择：在训练初期，避免使用如OneCycleLR这类固定epoch数量的学习率调整策略。由于损失下降趋势无法预先确定，且epoch数量可能会变化，一成不变的策略可能不如其他方法有效。

**学习率调整：**建议初始阶段采用步进式(step-wise)降低学习率的方法。如果发现损失下降幅度有限，可以暂停训练，调低学习率后继续（resume）。通过几轮训练，大致可以找到针对特定数据集和批处理大小的最优配置，然后在此基础上探索不同的网络结构或损失函数。

**热身策略：**制定合理的热身(warm-up)策略，包括初始学习率和迭代次数。

**优化器进阶调整：**如果采用SGD或ADAMw等优化器，除了学习率之外，也应考虑调整权重衰减(weight decay)等其他参数。

数据加载与损失计算优化：在加载真实标签(ground truth)数据和计算损失时，应尽量使用张量(tensor)操作，避免使用for循环。for循环会显著降低数据加载和损失计算的速度，从而拖慢整体训练进度。通常，采用现有的实现框架可以避免这一问题。

遵循以上建议，可以有效地优化占用网络的训练过程，提高实验效率