🥚误码

误码首先介绍误码的相关概念

🍔两种常见的检错技术

⭐奇偶校验

奇校验是在待发送的数据后面添加1个校验位，使得添加该校验位后的整个数据中比特1的个数为奇数
偶校验是在待发送的数据后面添加1个校验位，使得添加该校验位后的整个数据中比特1的个数为偶数

---

我们来看下面的例子

奇校验

偶校验

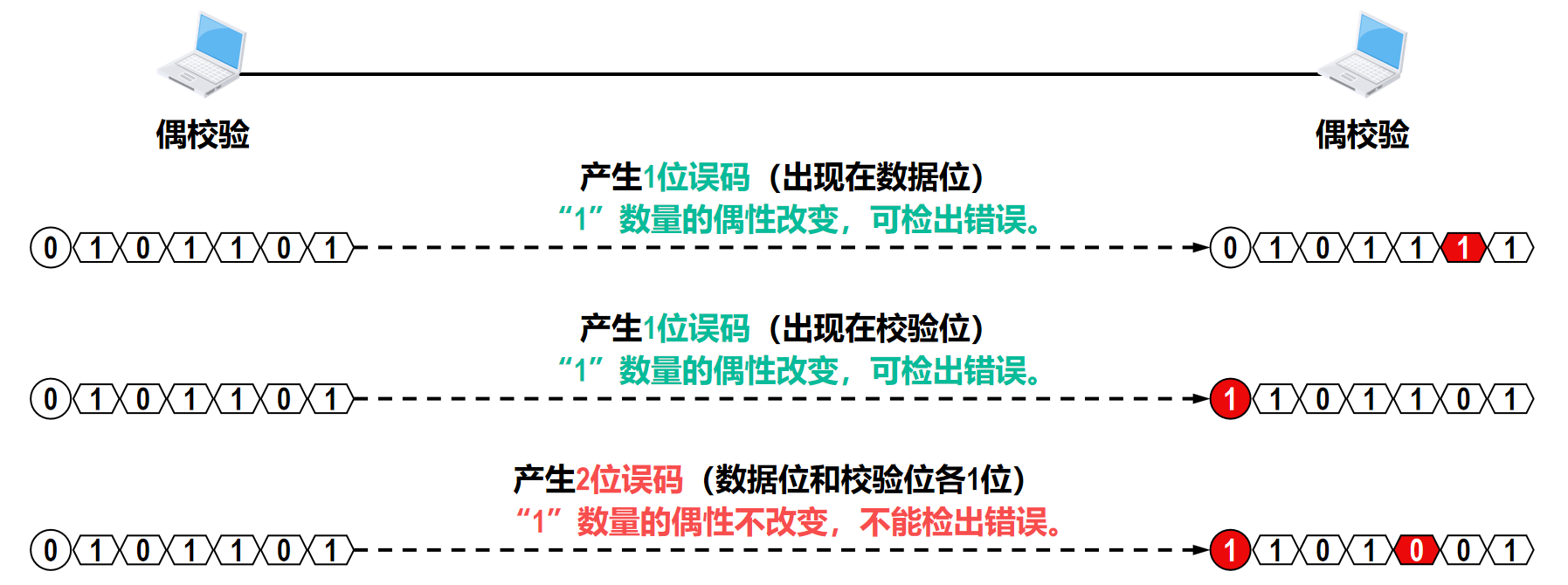
于是我们得到了下面的结论

在所传输的数据中，如果有奇数个位发生误码，则所包含比特1的数量的奇偶性会发生改变，可以检测出误码。
在所传输的数据中，如果有偶数个位发生误码，则所包含比特1的数量的奇偶性不会发生改变，无法检测出误码（漏检）。

⭐循环冗余校验

数据链路层广泛使用漏检率极低的循环冗余校验（Cyclic Redundancy Check，CRC）检错技术。
循环冗余校验CRC的基本思想：

收发双方约定好一个生成多项式G(X)。
发送方基于待发送的数据和生成多项式G(X)，计算出差错检测码（冗余码），将冗余码添加到待发送数据的后面一起传输。
接收方收到数据和冗余码后，通过生成多项式G(X)来计算收到的数据和冗余码是否产生了误码。

发送方CRC操作
如下图所示
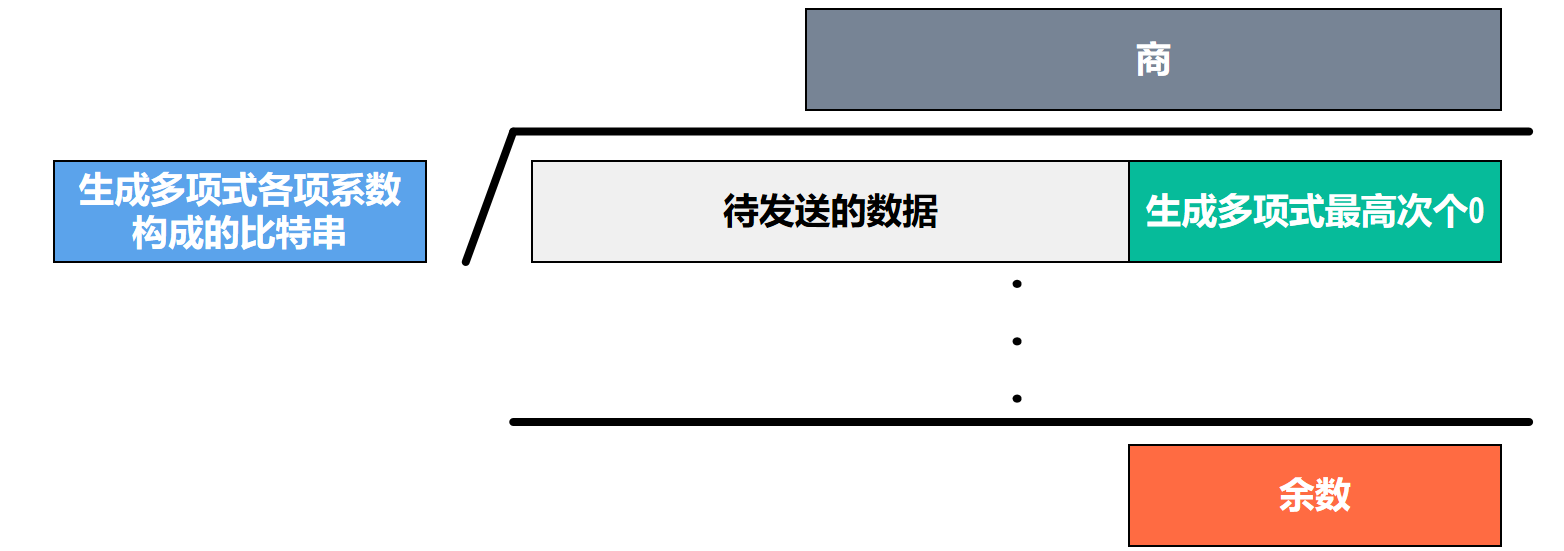进行除法，将待发送的数据作为被除数的一部分，后面添加生成多项式最高次个0以构成被除数。
生成多项式各项系数构成的比特串作为除数，进行除法，得到商和余数

将余数添加到发送数据的后面，一起发送。

注意：
商仅作为标记，防止计算过程对错位
余数的长度应与生成多项式最高次数相同，作为冗余码
这里的除法是指：二进制模2除法，二进制模2除法既不向上进位，也不比较除数和被除数的对应位数值的大小，只要以相同位数进行相除即可，相当于对应位进行逻辑异或运算

接收方CRC操作
如下图所示
与发送方类似，也要进行除法。
将收到的数据和冗余码作为被除数，生成多项式各项系数构成的比特串作为除数，进行除法，得到商和余数。
如果余数为0，就可判定数据和冗余码中没有出现误码，否则出现了误码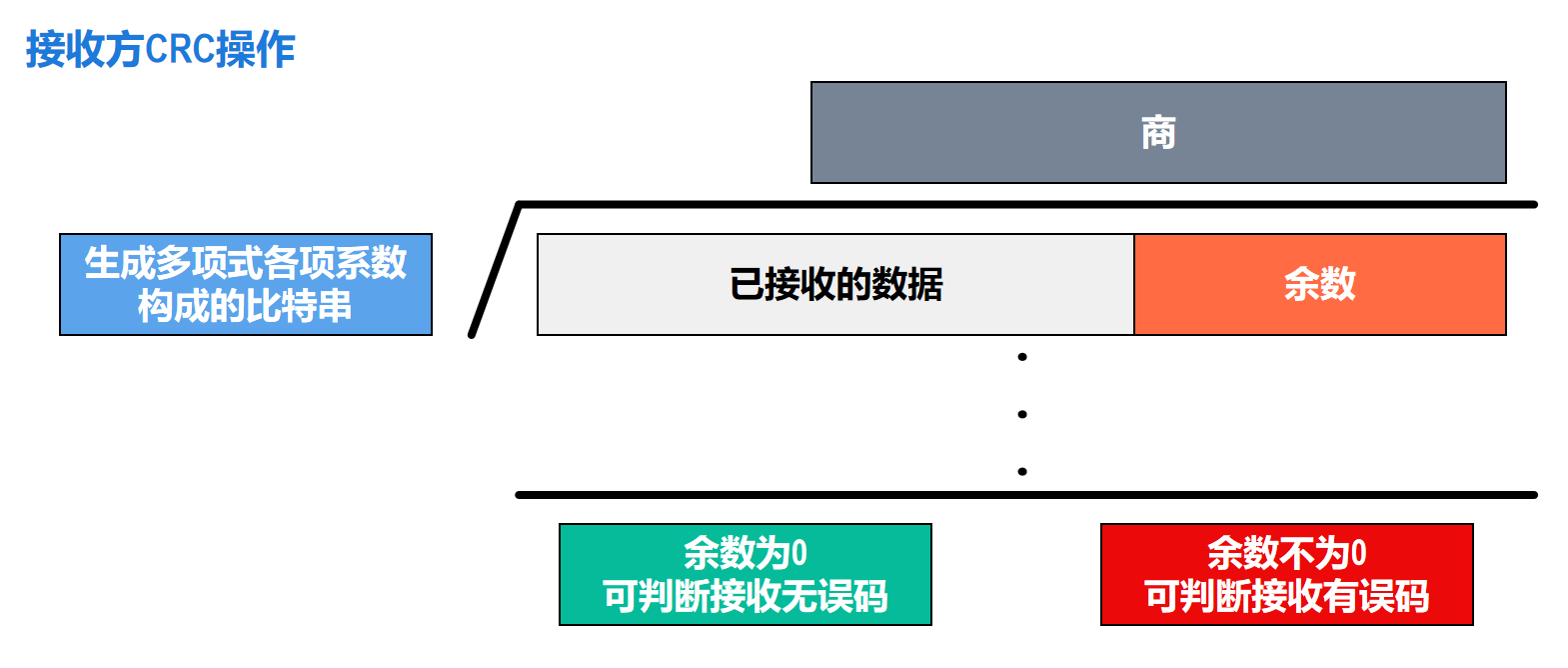生成多项式举例

🎈例子

发送方

将冗余码添加到待发送数据的后面进行发送

接收方

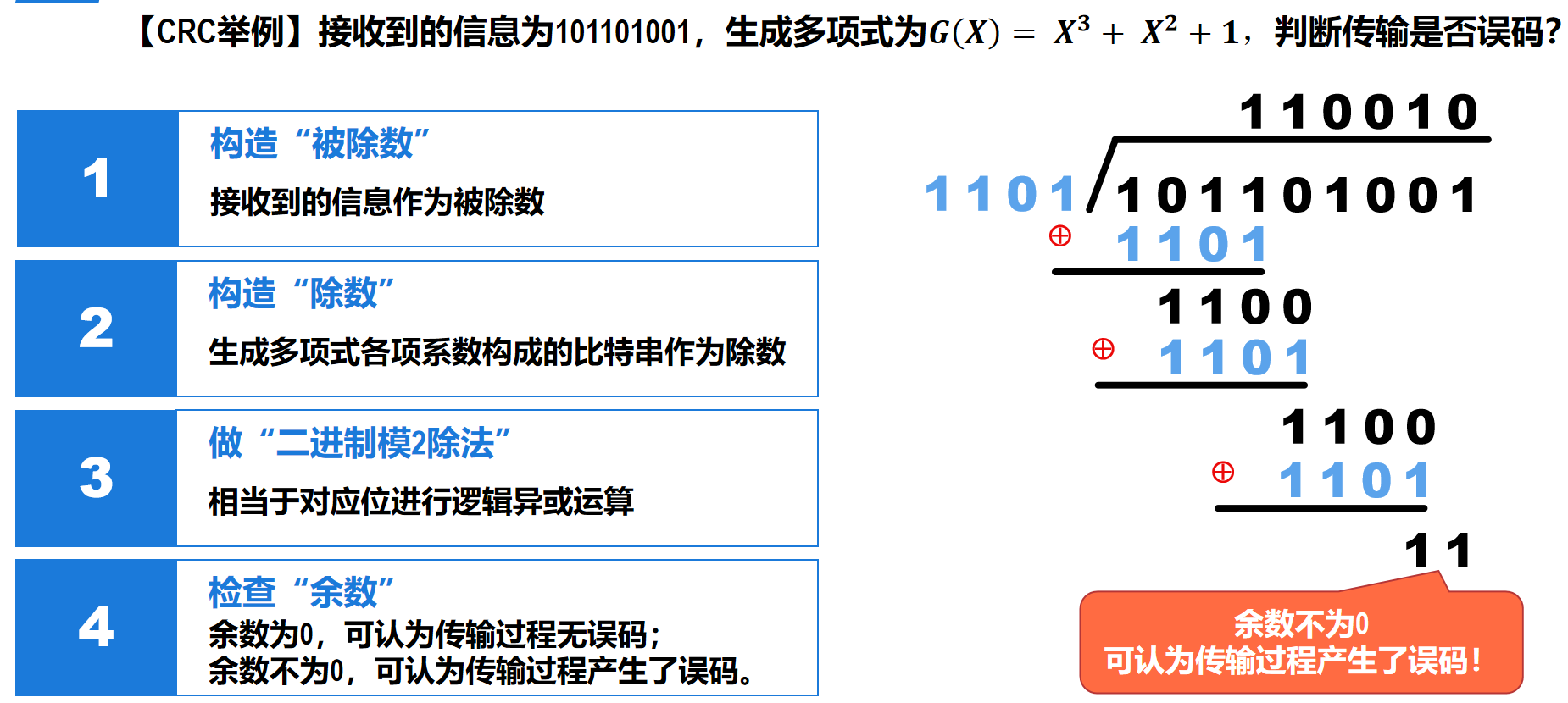
注意：

数据链路层的差错检测通常通过循环冗余检验（CRC）来实现。CRC是一种基于多项式除法的技术，用于对数据帧进行检验，以确定数据在传输过程中是否发生了错误。

在数据链路层，发送方在发送数据帧之前会计算出一个CRC码，并将其附加到数据帧的尾部。接收方在接收数据帧后，也会计算接收到的数据帧中的CRC码，然后与接收到的CRC码进行比较。如果两者不一致，则表明数据帧在传输过程中发生了错误。

通过CRC的差错检测，数据链路层能够及时发现数据帧中的比特错误，从而提高数据传输的可靠性。