目录
一、什么是FCN
1、FCN简介
2、核心思想
二、代码实现
1、FCN结构介绍
2、ResNet-18提取图像特征
3、1×1卷积层将通道数变换为类别个数
4、转置卷积还原输入图像的高和宽
5、初始化转置卷积层
6、读取数据集
7、训练
8、预测
三、总结
一、什么是FCN
1、FCN简介
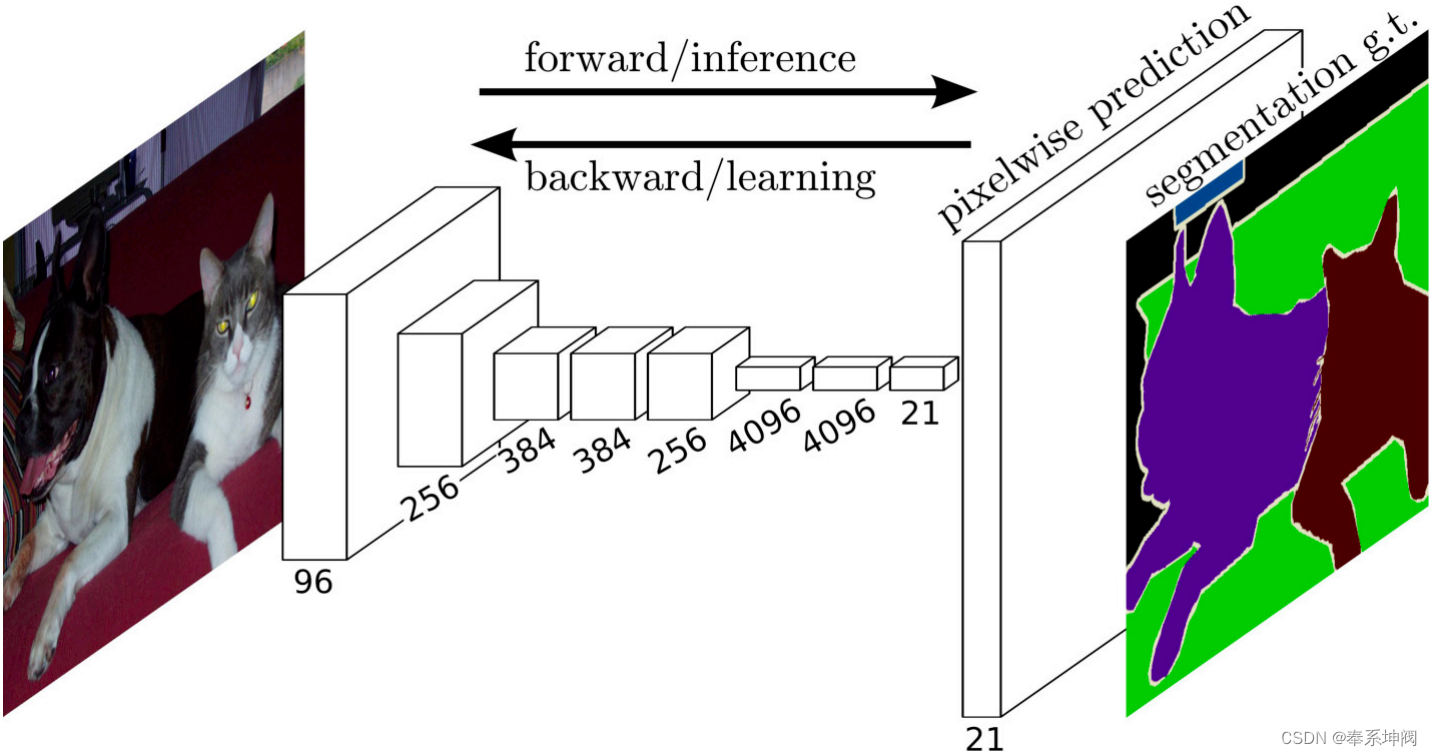
全卷积网络(Fully Convolutional Networks,FCN)是Jonathan Long等人于2015年在Fully Convolutional Networks for Semantic Segmentation一文中提出的用于图像语义分割的一种框架,是深度学习用于语义分割领域的开山之作。FCN将传统CNN后面的全连接层换成了卷积层,这样网络的输出将是热力图而非类别;同时,为解决卷积和池化导致图像尺寸的变小,使用上采样方式对图像尺寸进行恢复。
2、核心思想
- 不含全连接层的全卷积网络,可适应任意尺寸输入;
- 反卷积层增大图像尺寸,输出精细结果;
- 结合不同深度层结果的跳级结构,确保鲁棒性和精确性。
二、代码实现
1、FCN结构介绍
如fig1所示,全卷积网络先使用卷积神经网络抽取图像特征,然后通过卷积层将通道数变换为类别个数,最后再通过转置卷积层将特征图的高和宽变换为输入图像的尺寸。因此,模型输出与输入图像的高和宽相同,且最终输出通道包含了该空间位置像素的类别预测。
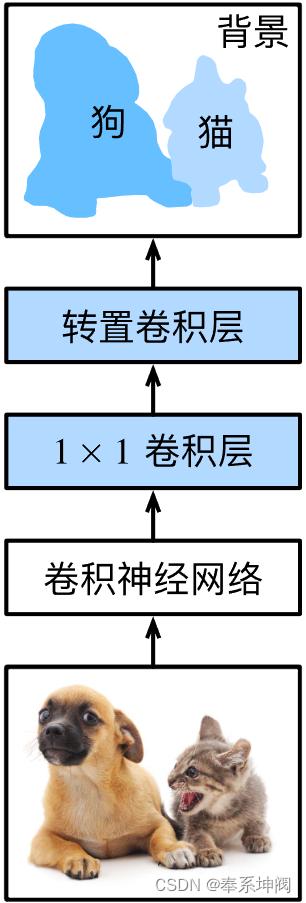
2、ResNet-18提取图像特征
下面,我们使用在ImageNet数据集上预训练的ResNet-18模型来提取图像特征,并将该网络记为pretrained_net。ResNet-18模型的最后几层包括全局平均池化层和全连接层,然而全卷积网络中不需要它们。
pretrained_net = torchvision.models.resnet18(pretrained=True)
# list(pretrained_net.children())
list(pretrained_net.children())[-3:] # .children()遍历模型的所有子层,[-3:]列出最后3层[Sequential(
(0): BasicBlock(
(conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
),
AdaptiveAvgPool2d(output_size=(1, 1)),
Linear(in_features=512, out_features=1000, bias=True)]可以看到最后一层是线性层,倒数第二层是全局平均池化层,倒数第三层是ResNet-18的一个block,因此最后两层是我们不需要的。关于Pytorch中.children()的用法可参考下面链接。
PyTorch中的modules()和children()相关函数简析 - 知乎目的: 介绍PyTorch中 model.modules(), model.named_modules(), model.children(), model.named_children(), model.parameters(), model.named_parameters(), model.state_dict()这些model实例方法的返回值。 例…![]() https://zhuanlan.zhihu.com/p/349156416
https://zhuanlan.zhihu.com/p/349156416
接下来,我们创建一个全卷积网络`net`。它复制了ResNet-18中大部分的预训练层,除了最后的全局平均池化层和最接近输出的全连接层。
net = nn.Sequential(*list(pretrained_net.children())[:-2]) 给定高度为320和宽度为480的输入,`net`的前向传播将输入的高和宽减小至原来的,即10和15。
X = torch.rand(size=(1, 3, 320, 480))
net(X).shapetorch.Size([1, 512, 10, 15])3、1×1卷积层将通道数变换为类别个数
接下来使用卷积层将输出通道数转换为Pascal VOC2012数据集的类数(21类,包括背景)。最后需要将特征图的高度和宽度增加32倍,从而将其变回输入图像的高和宽。
回想一下转置卷积中计算输出形状的结论:我们可以看到如果步幅为,填充为
(假设
是整数)且卷积核的高和宽为
,转置卷积会将输入的高和宽分别放大
倍。由于
且
,我们构造一个步幅为
的转置卷积层,并将卷积核的高和宽设为
,填充为
。
num_classes = 21
net.add_module('final_conv', nn.Conv2d(512, num_classes, kernel_size=1))4、转置卷积还原输入图像的高和宽
net.add_module('transpose_conv', nn.ConvTranspose2d(num_classes, num_classes,
kernel_size=64, padding=16, stride=32))5、初始化转置卷积层
在图像处理中,我们有时需要将图像放大,即上采样(upsampling)。双线性插值(bilinear interpolation)是常用的上采样方法之一,它也经常用于初始化转置卷积层。
为了解释双线性插值,假设给定输入图像,我们想要计算上采样输出图像上的每个像素。
- 将输出图像的坐标
映射到输入图像的坐标
上。例如,根据输入与输出的尺寸之比来映射。请注意,映射后的
和
是实数。
- 在输入图像上找到离坐标
最近的4个像素。
- 输出图像在坐标
上的像素依据输入图像上这4个像素及其与
的相对距离来计算。
双线性插值的上采样可以通过转置卷积层实现,内核由以下bilinear_kernel函数构造。限于篇幅,我们只给出bilinear_kernel函数的实现,不讨论算法的原理。
def bilinear_kernel(in_channels, out_channels, kernel_size):
factor = (kernel_size + 1) // 2
if kernel_size % 2 == 1:
center = factor - 1
else:
center = factor - 0.5
og = (torch.arange(kernel_size).reshape(-1, 1),
torch.arange(kernel_size).reshape(1, -1))
filt = (1 - torch.abs(og[0] - center) / factor) * \
(1 - torch.abs(og[1] - center) / factor)
weight = torch.zeros((in_channels, out_channels,
kernel_size, kernel_size))
weight[range(in_channels), range(out_channels), :, :] = filt
return weight让我们用双线性插值的上采样实验它由转置卷积层实现。我们构造一个将输入的高和宽放大2倍的转置卷积层,并将其卷积核用bilinear_kernel函数初始化。
conv_trans = nn.ConvTranspose2d(3, 3, kernel_size=4, padding=1, stride=2,
bias=False)
conv_trans.weight.data.copy_(bilinear_kernel(3, 3, 4))tensor([[[[0.0625, 0.1875, 0.1875, 0.0625],
[0.1875, 0.5625, 0.5625, 0.1875],
[0.1875, 0.5625, 0.5625, 0.1875],
[0.0625, 0.1875, 0.1875, 0.0625]],
[[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000]]],
[[[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000]],
[[0.0625, 0.1875, 0.1875, 0.0625],
[0.1875, 0.5625, 0.5625, 0.1875],
[0.1875, 0.5625, 0.5625, 0.1875],
[0.0625, 0.1875, 0.1875, 0.0625]],
[[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000]]],
[[[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000]],
[[0.0625, 0.1875, 0.1875, 0.0625],
[0.1875, 0.5625, 0.5625, 0.1875],
[0.1875, 0.5625, 0.5625, 0.1875],
[0.0625, 0.1875, 0.1875, 0.0625]]]])读取图像`X`,将上采样的结果记作`Y`。为了打印图像,我们需要调整通道维的位置。
img = torchvision.transforms.ToTensor()(d2l.Image.open('../img/catdog.jpg'))
X = img.unsqueeze(0)
Y = conv_trans(X)
out_img = Y[0].permute(1, 2, 0).detach()可以看到,转置卷积层将图像的高和宽分别放大了2倍。
d2l.set_figsize()
print('input image shape:', img.permute(1, 2, 0).shape)
d2l.plt.imshow(img.permute(1, 2, 0))
print('output image shape:', out_img.shape)
d2l.plt.imshow(out_img)input image shape: torch.Size([561, 728, 3])
output image shape: torch.Size([1122, 1456, 3])
<matplotlib.image.AxesImage at 0x1c1aee9c520>
全卷积网络用双线性插值的上采样初始化转置卷积层。对于卷积层,我们使用Xavier初始化参数。
W = bilinear_kernel(num_classes, num_classes, 64)
net.transpose_conv.weight.data.copy_(W)tensor([[[[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
...,
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
...,
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]]],
[[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
...,
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
...,
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]]],
[[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
...,
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002]],
...,
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]]],
...,
[[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
...,
[[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
...,
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]]],
[[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
...,
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
...,
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]]],
[[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
...,
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
[[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
...,
[0.0012, 0.0037, 0.0061, ..., 0.0061, 0.0037, 0.0012],
[0.0007, 0.0022, 0.0037, ..., 0.0037, 0.0022, 0.0007],
[0.0002, 0.0007, 0.0012, ..., 0.0012, 0.0007, 0.0002]]]])6、读取数据集
指定随机裁剪的输出图像的形状为:高和宽都可以被
整除。
batch_size, crop_size = 32, (320, 480)
train_iter, test_iter = d2l.load_data_voc(batch_size, crop_size)7、训练
现在我们可以训练全卷积网络了。这里的损失函数和准确率计算与图像分类中的并没有本质上的不同,因为我们使用转置卷积层的通道来预测像素的类别,所以需要在损失计算中指定通道维。此外,模型基于每个像素的预测类别是否正确来计算准确率。
def loss(inputs, targets):
return F.cross_entropy(inputs, targets, reduction='none').mean(1).mean(1)
num_epochs, lr, wd, devices = 5, 0.001, 1e-3, d2l.try_all_gpus()
trainer = torch.optim.SGD(net.parameters(), lr=lr, weight_decay=wd)
d2l.train_ch13(net, train_iter, test_iter, loss, trainer, num_epochs, devices)loss 0.443, train acc 0.863, test acc 0.848
254.0 examples/sec on [device(type='cuda', index=0), device(type='cuda', index=1)]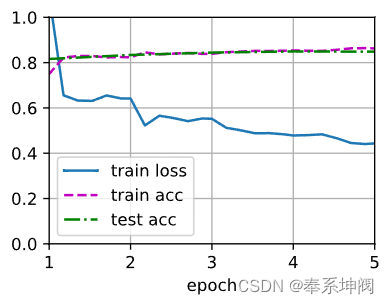
8、预测
在预测时,我们需要将输入图像在各个通道做标准化,并转成卷积神经网络所需要的四维输入格式。
def predict(img):
X = test_iter.dataset.normalize_image(img).unsqueeze(0)
pred = net(X.to(devices[0])).argmax(dim=1)
return pred.reshape(pred.shape[1], pred.shape[2])为了可视化预测的类别给每个像素,我们将预测类别映射回它们在数据集中的标注颜色。
def label2image(pred):
colormap = torch.tensor(d2l.VOC_COLORMAP, device=devices[0])
X = pred.long()
return colormap[X, :] 测试数据集中的图像大小和形状各异。由于模型使用了步幅为32的转置卷积层,因此当输入图像的高或宽无法被32整除时,转置卷积层输出的高或宽会与输入图像的尺寸有偏差。为了解决这个问题,我们可以在图像中截取多块高和宽为32的整数倍的矩形区域,并分别对这些区域中的像素做前向传播。请注意,这些区域的并集需要完整覆盖输入图像。当一个像素被多个区域所覆盖时,它在不同区域前向传播中转置卷积层输出的平均值可以作为`softmax`运算的输入,从而预测类别。为简单起见,我们只读取几张较大的测试图像,并从图像的左上角开始截取形状为的区域用于预测。对于这些测试图像,我们逐一打印它们截取的区域,再打印预测结果,最后打印标注的类别。
voc_dir = d2l.download_extract('voc2012', 'VOCdevkit/VOC2012')
test_images, test_labels = d2l.read_voc_images(voc_dir, False)
n, imgs = 4, []
for i in range(n):
crop_rect = (0, 0, 320, 480)
X = torchvision.transforms.functional.crop(test_images[i], *crop_rect)
pred = label2image(predict(X))
imgs += [X.permute(1,2,0), pred.cpu(),
torchvision.transforms.functional.crop(
test_labels[i], *crop_rect).permute(1,2,0)]
d2l.show_images(imgs[::3] + imgs[1::3] + imgs[2::3], 3, n, scale=2)
三、总结
- 全卷积网络先使用卷积神经网络抽取图像特征,然后通过
卷积层将通道数变换为类别个数,最后通过转置卷积层将特征图的高和宽变换为输入图像的尺寸。
- 在全卷积网络中,我们可以将转置卷积层初始化为双线性插值的上采样。