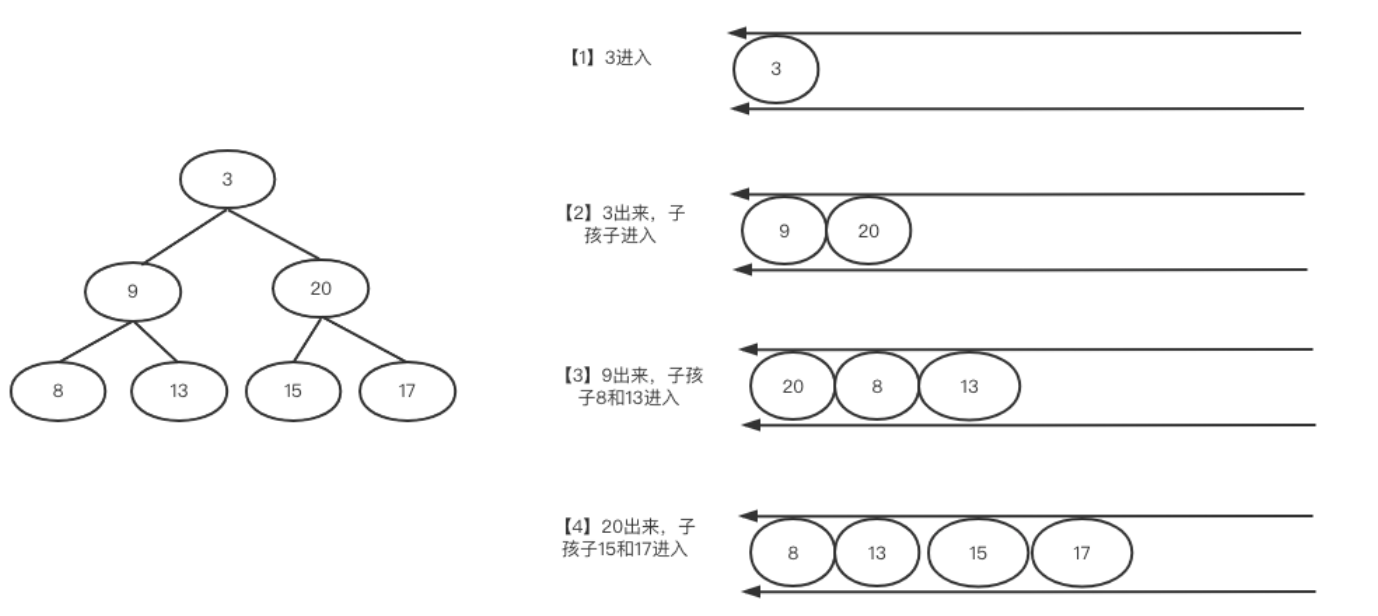
问题描述：

---

解题思路：

        一个数也可以看作是一段区间，当该区间的异或和为完全平方数时则符合题意。

        我们需要注意枚举的完全平方的上限。

        异或前缀和减小时间复杂度。

---

题解：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e4 + 9;

int a[N],cnt[N << 2];  // cnt要开大点，因为cnt[(j * j) ^ a[i]]给j*j开的范围是n << 1, 所以(n << 1) ^ a[i]时，为了保证上限不溢出再往左一位，n << 1 << 1 == n << 2

int main()
{
  ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
  int n;cin >> n;
  for(int i = 1; i <= n; i++)cin >> a[i];


  for(int i = 1; i <= n; i++)  // 异或前缀和
  {
    a[i] = a[i] ^ a[i - 1];
  }

  ll ans = 0;
  cnt[0]++;  // 前缀和0和i位置的异或值代表原数组1~i的异或值,子数组只有一个数的情况也算进去 
  for(int i = 1; i <= n; i++)
  {
   
    for(int j = 0; j * j <= n << 1; j++)  // n<<1是因为数组二进制异或最大不会超过n位，让n左移一位开大点无妨 
    {
      ans += cnt[(j * j) ^ a[i]];
    // 枚举全部完全平方，0~i位置异或结果为完全平方数加入 
    }
    cnt[a[i]]++;  // 为了防止混乱，没枚举到的i位置默认没有，计数为0 （每次遍历的区间上限为i） 

  }
	
  cout << (n*(n + 1))/2 - ans << '\n';
  return 0;
}

---

知识点：异或