二叉树的层次遍历经典问题-算法通关村

---

1 层次遍历简介

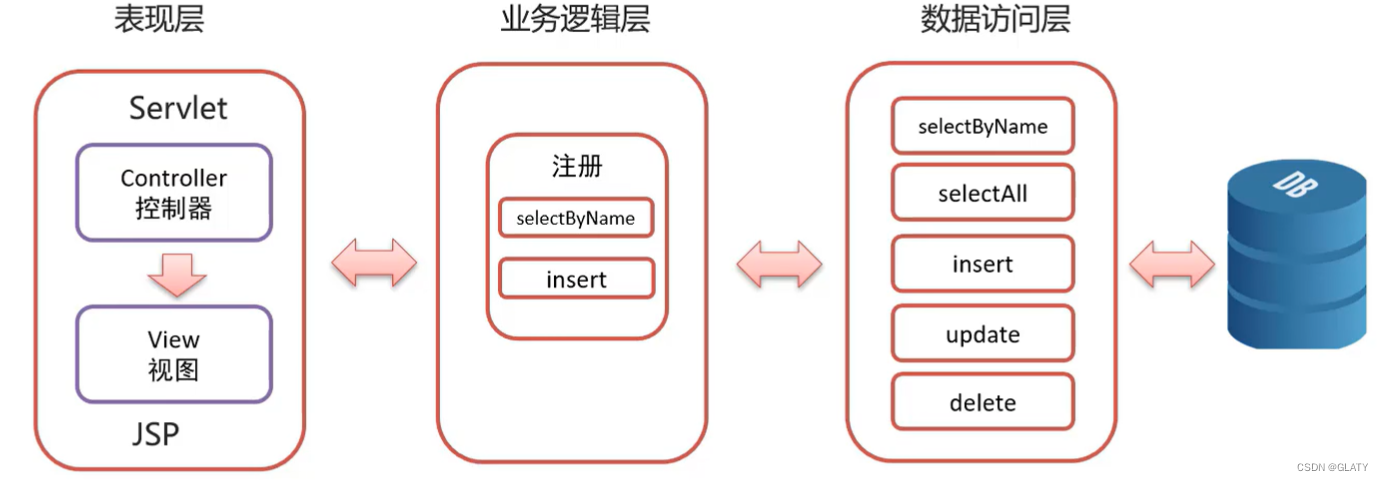
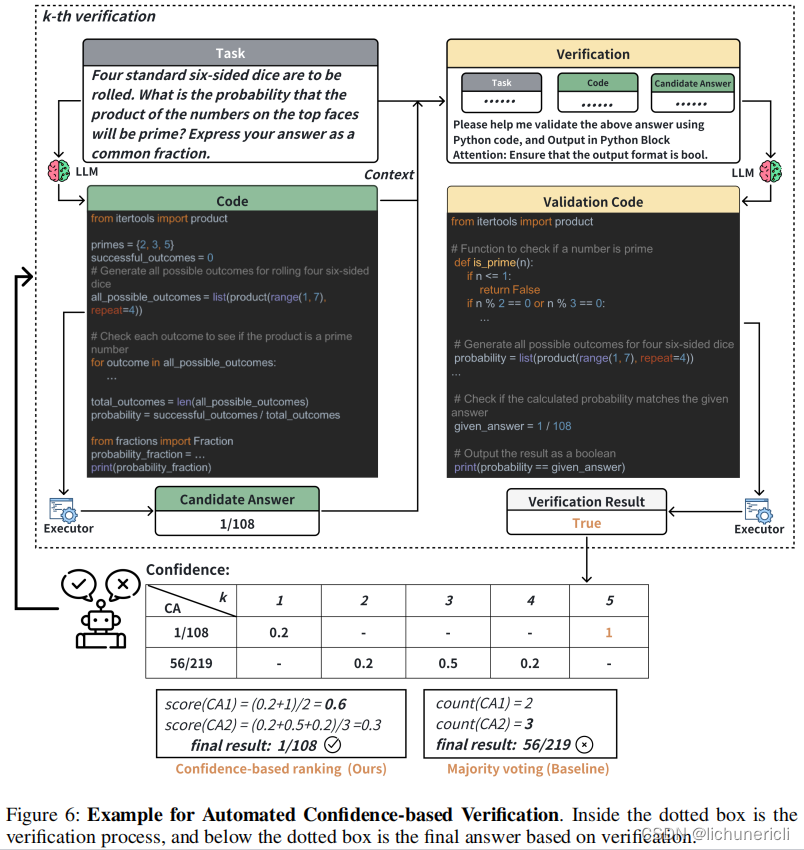
• 广度优先在面试里出现的频率非常高，整体属于简单题。广度优先又叫层次遍历，基本过程如下：

• 

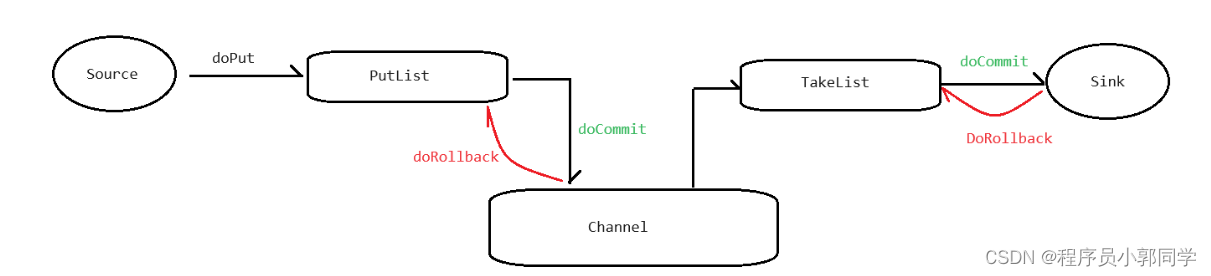
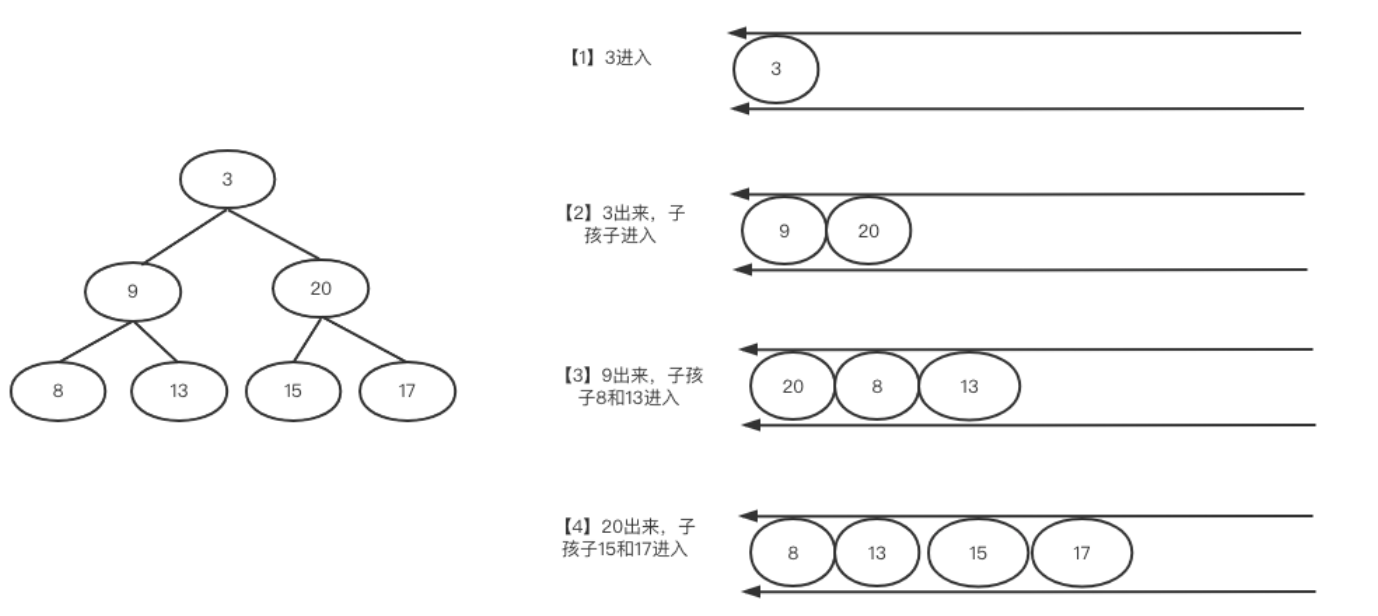
• 层次遍历就是从根节点开始，先访问根节点下面一层全部元素，再访问之后的层次，类似金字塔一样一层层访问。我们可以看到这里就是从左到右一层一层的去遍历二叉树，先访问3，之后访问3的左右子孩子9和20，之后分别访问9和20的左右子孩子［8,13］和［15，17］，最后得到结果
  ［3,9,20,8,13,15,17］。
  这里的问题是怎么将遍历过的元素的子孩子保存一下呢，例如访问9时其左右子孩子8和13应该先存一下，直到处理20之后才会处理。使用队列来存储能完美解决上述问题，例如上面的图中：

• 1. 首先3入队 2.然后3出队，之后将3的左右孩子9和20，保存到队列中。 3.之后9出队，将9的左右孩子8和13入队。 4.之后20出队，将20的左右孩子15和7入队。 5.之后 8,13,15,7分别出队，此时都是叶子结点，只出队就行。

• 这就是LeetCode里经典的层次遍历题！102.二叉树的层序遍历，107.二叉树的层次遍历II，199.二叉树的右视图，637.二叉树的层平均值，429.N叉树的前序遍历，515.在每个树行中找最大值，116.填充每个节点的下一个右侧节点指针，117.填充每个节点的下一个右侧节点指针II，103 锯齿层序遍历
  除此之外，在深度优先的题目里，有些仍然会考虑层次遍历的实现方法。

---

2 基本的层序遍历与变换

• 仅仅遍历并输出全部元素

• 

•   public List<Integer> simpleLevelOrder(TreeNode root){
           if(root == null){
               return new ArrayList<Integer>();
           }
           List<Integer> list = new ArrayList<>();
           Deque<TreeNode> TreeQueue = new ArrayDeque<>();
           //将根节点放入队列中，然后不断遍历
           TreeQueue.offer(root);
           while(!TreeQueue.isEmpty()){
               //一层一层的遍历
               for(int i = 0; i< TreeQueue.size(); i++){
                   TreeNode temp = TreeQueue.poll();
                   list.add(temp.val);
                   if(temp.left != null){
                       TreeQueue.offer(temp.left);
                   }
                   if(temp.right != null){
                       TreeQueue.offer(temp.right);
                   }
               }
           }
           return list;
        }
  

---

2.1二叉树的层序遍历

• LeetCode102：给你一个二叉树，请你返回其按层次遍历得到的节点值。（即逐层地，从左到右访问所有节点）。

• 

• 如何判断某一层访问完了呢？简单，用一个变量size标记一下就行了，size表示某一层的元素个数，只要出队，就将size减1，减到O就说明该层元素访问完了。当size变成0之后，这时队列中剩余元素的个数恰好就是下一层元素的个数，因此重新将size标记为下一层的元素个数就可以继续处理新的一行了。最后，把每层遍历到的节点都放到一个结果集中，将其返回就行了。

•   public List<List<Integer>> levelOrder(TreeNode root){
            if(root == null){
                return new ArrayList<List<Integer>>();
            }
            List<List<Integer>> res = new ArrayList<>();
            Deque<TreeNode> TreeQueue = new ArrayDeque<>();
            //将根节点放入队列中，然后不断遍历
            TreeQueue.offer(root);
            while(!TreeQueue.isEmpty()){
                //存储每一层的元素
                List<Integer> list = new ArrayList<>();
                for(int i = 0; i< TreeQueue.size(); i++){
                    TreeNode temp = TreeQueue.poll();
                    list.add(temp.val);
                    if(temp.left != null){
    
                        TreeQueue.offer(temp.left);
                    }
                    if(temp.right != null){
                        TreeQueue.offer(temp.right);
                    }
                }
                res.add(list);
            }
            return res;
        }
  

---

2.2 层序遍历-自底向上

• LeetCode 107.给定一个二叉树，返回其节点值自底向上的层序遍历。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）。例如给定的二叉树为：

• 

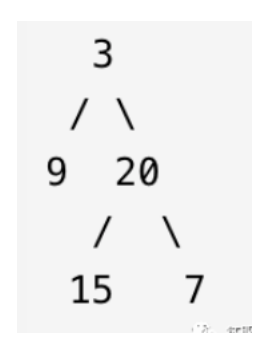
• [ [15, 7], [9, 20], [3] ]

• 如果要求从上到下输出每一层的节点值，做法是很直观的，在遍历完一层节点之后，将存储该层节点值的列表添加到结果列表的尾部。这道题要求从下到上输出每一层的节点值，只要对上述操作稍作修改即可，在遍历完一层节点之后，将存储该层节点值的列表添加到结果列表的头部。

•   public List<List<Integer>> levelOrderBottom(TreeNode root){
            if(root == null){
                return new ArrayList<List<Integer>>();
            }
            List<List<Integer>> res = new ArrayList<>();
            Deque<TreeNode> TreeQueue = new ArrayDeque<>();
            //将根节点放入队列中，然后不断遍历
            TreeQueue.offer(root);
            while(!TreeQueue.isEmpty()){
                //存储每一层的元素
                List<Integer> levelList = new ArrayList<>();
                for(int i = 0; i< TreeQueue.size(); i++){
                    TreeNode temp = TreeQueue.poll();
                    levelList.add(temp.val);
                    if(temp.left != null){
    
                        TreeQueue.offer(temp.left);
                    }
                    if(temp.right != null){
                        TreeQueue.offer(temp.right);
                    }
                }
                //当前层的节点值列表 levelList 添加到结果列表 res 的开头，
                // 实现了层次遍历结果的逆序存储。
                res.add(0, levelList);
            }
            return res;
        }
  

---

2.3二叉树的锯齿形层序遍历

• LeetCode103 ：给定一个二叉树，返回其节点值的锯齿形层序遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。
  例如：给定二叉树 ［3,9,20,null,null,15,7］

• 

• [ [3], [20, 9] [15, 7] ]

• 这个题也是102的变种，只是最后输出的要求有所变化，要求我们按层数的奇偶来决定每一层的输出顺序。如果当前层数是偶数，从左至右输出当前层的节点值，否则，从右至左输出当前层的节点值。

• 我们依然可以沿用第102题的思想，为了满足题目要求的返回值为**「先从左往右，再从右往左」交替输出的锯齿形，可以利用「双端队列」**的数据结构来维护当前层节点值输出的顺序。双端队列是一个可以在队列任意一端插入元素的队列。在广度优先搜索遍历当前层节点拓展下一层节点的时候我们仍然从左往右按顺序拓展，但是对当前层节点的存储我们维护一个变量isOrderLeft
  记录是从左至右还是从右至左的：
  • 如果从左至右，我们每次将被遍历到的元素插入至双端队列的末尾。
  •从右至左，我们每次将被遍历到的元素插入至双端队列的头部。

•   public List<List<Integer>> zigzagLevelOrder(TreeNode root){
            if(root == null){
                return new ArrayList<List<Integer>>();
            }
            List<List<Integer>> res = new ArrayList<>();
            Deque<TreeNode> TreeQueue = new ArrayDeque<>();
            //将根节点放入队列中，然后不断遍历
            TreeQueue.offer(root);
            boolean isOrderLeft = true;
            while(!TreeQueue.isEmpty()){
                //存储每一层的元素
                Deque<Integer> levelQueue = new ArrayDeque<>();
                for(int i = 0; i< TreeQueue.size(); i++){
                    TreeNode temp = TreeQueue.poll();
                    if(isOrderLeft){
                        levelQueue.addLast(temp.val);
                    }else{
                        levelQueue.addFirst(temp.val);
                    }
                    if(temp.left != null){
                        TreeQueue.offer(temp.left);
                    }
                    if(temp.right != null){
                        TreeQueue.offer(temp.right);
                    }
                }
                res.add(new ArrayList<Integer>(levelQueue));
                isOrderLeft = !isOrderLeft;
            }
            return res;
        }
  

---

2.4 N 叉树的层序遍历

• LeetCode429 给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。树的序列化输入是用层序遍历，每组子节点都由 null值分隔（参见示例）。

• 

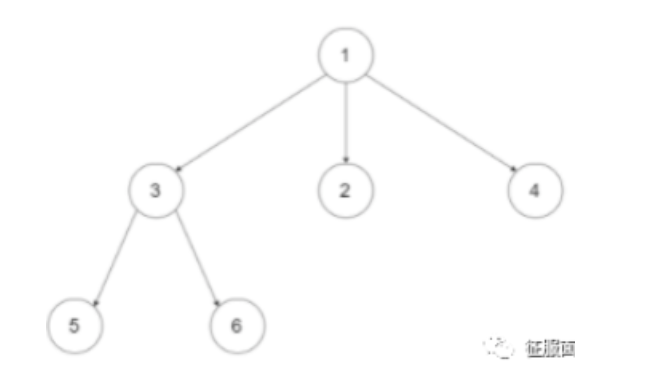
• 输入：root = [ 1, null, 3, 2, 4, null, 5, 6]（表述树的元素是这个序列） 输出：[ [1] ，[3,2,4]，[5,61] ]

• N 叉树的定义如下，就是一个值，加一个列表。

•   public class Node {
        public int val;
        public List<Node> children;
    }
  

•   public List<List<Integer>> nLevelOrder(Node root){
            if(root == null){
                return new ArrayList<List<Integer>>();
            }
            List<List<Integer>> res = new ArrayList<>();
            Deque<Node> NTreeQueue = new ArrayDeque<>();
            NTreeQueue.offer(root);
            while(!NTreeQueue.isEmpty()){
                List<Integer> levelList = new ArrayList<>();
                while(!NTreeQueue.isEmpty()){
                    Node cur = NTreeQueue.pollFirst();
                    levelList.add(cur.val);
                    for (Node child : cur.children) {
                        if(child != null){
                            NTreeQueue.add(child);
                        }
                    }
                }
                res.add(levelList);
            }
            return res;
        }
  

---

3 几个处理每层元素的项目

• LeetCode三道题目：515.在每个树行中找最大值（最小），637.二叉树的层平均值，199.二叉树的右视图。

3.1 在每个树行中找最大值

• LeetCode515: 给定一棵二叉树的根节点 root，请找出该二叉树中每一层的最大值。

• 

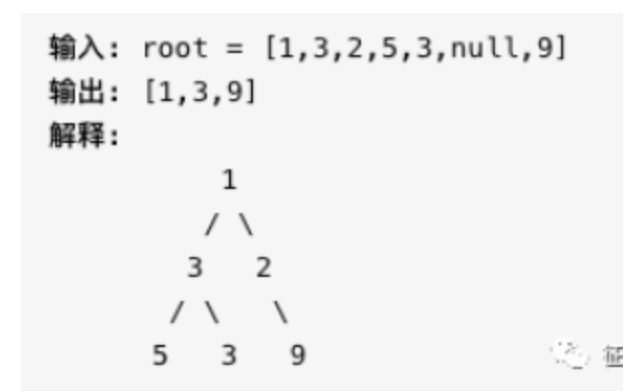
• 在得到一层的元素之后，用一个变量记录其最大值。

•   public List<Integer> largestValues(TreeNode root){
            if(root == null){
                return new ArrayList<Integer>();
            }
           List<Integer> res = new ArrayList<>();
            Deque<TreeNode> TreeQueue = new ArrayDeque<>();
            //将根节点放入队列中，然后不断遍历
            TreeQueue.offer(root);
            while(!TreeQueue.isEmpty()){
                //存储每一层的元素
                int levelMaxNum = Integer.MIN_VALUE;
                for(int i = 0; i< TreeQueue.size(); i++){
                    TreeNode temp = TreeQueue.poll();
                    levelMaxNum = Math.max(levelMaxNum, temp.val);
                    if(temp.left != null){
                        TreeQueue.offer(temp.left);
                    }
                    if(temp.right != null){
                        TreeQueue.offer(temp.right);
                    }
                }
                res.add(levelMaxNum);
            }
            return res;
        }
  

---

3.2 在每个树行中找平均值

• LeetCode637：要求给定一个非空二叉树，返回一个由每层节点平均值组成的数组。

• 

• 将每层的元素都先保存下来，最后求平均值。

•   public List<Double> averageOfLevels(TreeNode root){
            if(root == null){
                return new ArrayList<Double>();
            }
            List<Double> res = new ArrayList<>();
            Deque<TreeNode> TreeQueue = new ArrayDeque<>();
            //将根节点放入队列中，然后不断遍历
            TreeQueue.offer(root);
            while(!TreeQueue.isEmpty()){
                double levelAverage = 0;
                int len = TreeQueue.size();
                for(int i = 0; i< len; i++){
                    TreeNode temp = TreeQueue.poll();
                    levelAverage += temp.val;
                    if(temp.left != null){
                        TreeQueue.offer(temp.left);
                    }
                    if(temp.right != null){
                        TreeQueue.offer(temp.right);
                    }
                }
                res.add(levelAverage/len);
            }
            return res;
        }
  

---

3.3 二叉树的右视图

• LeetCode 199：给定一个二叉树的根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。例如：

• 

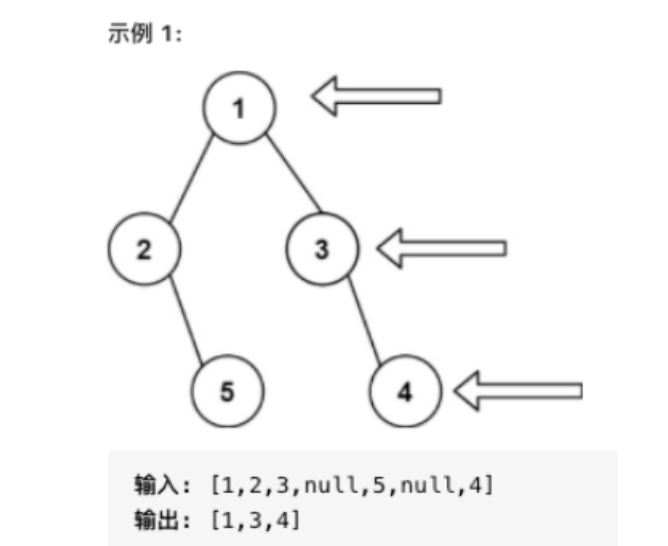
• 利用BFS进行层次遍历，记录下每层的最后一个元素。

•   public List<Integer> rightSideView(TreeNode root){
            if(root == null){
                return new ArrayList<Integer>();
            }
            List<Integer> res = new ArrayList<>();
            Deque<TreeNode> TreeQueue = new ArrayDeque<>();
            //将根节点放入队列中，然后不断遍历
            TreeQueue.offer(root);
            while(!TreeQueue.isEmpty()){
                int len = TreeQueue.size();
                int rightValue = 0;
                for(int i = 0; i< len; i++){
                    TreeNode temp = TreeQueue.poll();
                    if(i == len-1){
                        rightValue = temp.val;
                    }
                    if(temp.left != null){
                        TreeQueue.offer(temp.left);
                    }
                    if(temp.right != null){
                        TreeQueue.offer(temp.right);
                    }
                }
                res.add(rightValue);
            }
            return res;
        }
  

---

3.4 最底层最左边

• LeetCode513: 给定一个二叉树的 根节点root，请找出该二叉树的 最底层 最左边 节点的值。

• 

• 假设二叉树中至少有一个节点。

• 示例1：
  输入：root = [2, 1, 3] 输出：1
  示例2：
  输入：[1, 2, 3, 4, null, 5, 6, null, null, 7] 输出：7

• 这里有两个问题：该怎么知道什么时候到了最底层呢？假如最底层有两个，该怎么知道哪个是最左的呢？我们继续观察层次遍历的执行过程：

• 

• 我们可以发现，正常执行层次遍历，不管最底层有几个元素，最后一个输出的一定是是最底层最右的元素7，那这里我们就想了，能否将该处理与上一次题的翻转结合一下，每一层都是先反转再放入队列，就可以让最后一个输出的是最左的呢？是的，这就是解决本题的关键。

•   public int findBottomLeftValue(TreeNode root){
            if(root.right == null && root.left == null){
                return root.val;
            }
            Deque<TreeNode> TreeQueue = new ArrayDeque<>();
            TreeQueue.offer(root);
            TreeNode temp = new TreeNode();
            while(!TreeQueue.isEmpty()){
                int len = TreeQueue.size();
                for(int i = 0; i< len; i++){
                    temp = TreeQueue.poll();
                    //右节点先入队
                    if(temp.right != null){
                        TreeQueue.offer(temp.right);
                    }
                    //左节点后入队
                    if(temp.left != null){
                        TreeQueue.offer(temp.left);
                    }
                }
            }
            return temp.val;
        }
  

• 下面这个没有上面简洁，而且相比之下增加了一些额外的开销，仅供参考：

•   public int findBottomLeftValue2(TreeNode root){
            if(root.right == null && root.left == null){
                return root.val;
            }
            Deque<TreeNode> TreeQueue = new ArrayDeque<>();
            TreeQueue.offer(root);
            int res = 0;
            while(!TreeQueue.isEmpty()){
                int len = TreeQueue.size();
                Deque<TreeNode> queue = new ArrayDeque<>();
                for(int i = 0; i< len; i++){
                    TreeNode temp = TreeQueue.poll();
                    queue.addFirst(temp);
                    if(temp.left != null){
                        TreeQueue.offer(temp.left);
                    }
                    if(temp.right != null){
                        TreeQueue.offer(temp.right);
                    }
                }
                res = queue.removeLast().val;
            }
            return res;
        }