简介
贪心算法(Greedy Algorithm)是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是全局最好或最优的算法。也就是首先选取局部最优,从局部最优推出全局最优。
举例
有一堆不同面额的钞票,要从中取十次,要求最后的总金额最大。我们当然是每次都去取最大面额的钞票,最终的总金额才是最大。
特点
贪心算法的题目有两种极端:第一种是比较简单的,这一种在解答时候会觉得就是常识,怎么还需要算法呢。第二种就是复杂类的。在此说明的原因是希望各位不要轻视贪心算法,这个算法没有那么简单。
题目示例
示例一:分发饼干
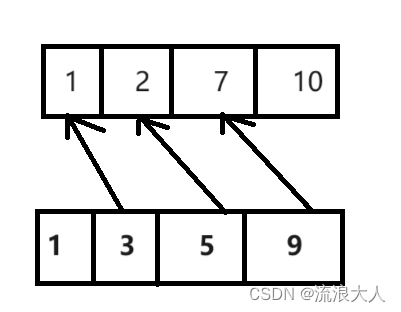
假设数组stomach=[1,2,7,10]表示的是孩子胃口的大小,数组cookie=[1,3,5,9]表示饼干大小,用这些饼干最多可以满足多少孩子(饼干的大小要大于小孩胃口才能满足孩子)。最终结果输出3.
要想满足上述条件,局部最优也应该是如下
public static int getResult(int[] stomach,int[] cookie){
//TODO 在最开始先将两个数组排序,此处示例是已经排好序的,故省略
//最终返回结果
int result = 0;
//该变量是饼干数组的最大索引
int index = cookie.length-1;
//在遍历匹配时应倒叙取遍历,因为最先匹配胃口最大的小孩(局部最优)
for (int i = stomach.length-1; i >= 0; i--) {
//获取到饼干数组的最后一个索引对应的数据,将该数据和stomacth数组的每一个数据比较
//注意:必须先比较索引不能为负数,如果调整while循环的位置,会出现异常情况
while (index>=0 && cookie[index]>=stomach[i]){
//记录此次结果
result++;
//饼干数组的索引往前移动一位
index--;
break;
}
}
return result;
}
public static void main(String[] args) {
int[] stomach={1,2,7,10};
int[] cookie={1,3,5,9};
int result = getResult(stomach, cookie);
System.out.println(result);
}示例二:摆动序列
给定数组arr,可以删除数组中的元素,问什么时候摆动序列最长。(摆动序列:相邻两个数的差值满足一正一负或一负一正)。
举例一:[1,7,4,9,2,5] ,后一个数字减去前一个数字的正负为:+ - + - +,所以原数组是摆动序列,输出6.
举例二:[1,17,5,10,13,15,10,5,16,8]。 输出结果:7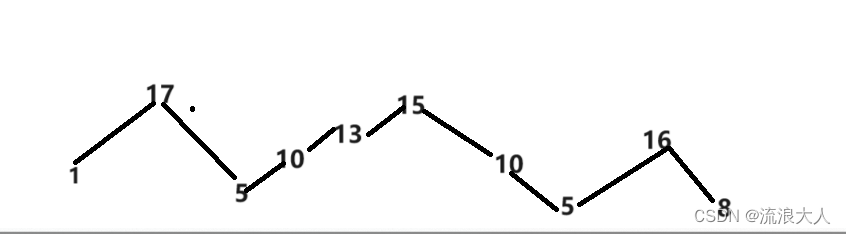
根据上图可知,要想满足摆动序列去删除元素,首先峰值的三个不能删除,只能删除在增长过程中的数据(局部最优)。
在编码时要考虑相同的情况
- 上下有p情况,如:[1,2,2,2,1]
- 首尾元素:如果数组中只有两个元素,且不相同,认为是两个摆动
- 单调过程中有平破,如:[1,2,2,3,4]
public static int getResult(int[] arr){
if (arr.length==1)return 1;
//前序差值
int preDiff = 0;
//后序差值
int curDiff = 0;
//默认最右端是有一个坡度的
int result = 1;
for (int i = 0; i < arr.length - 1; i++) {
curDiff = arr[i+1] - arr[i];
if ((preDiff>=0 && curDiff <0) || (preDiff<=0 && curDiff > 0)){
//因为最终是要返回摆动序列的长度,没有必要真正的去删除原数组中的数值
result++;
//当前数值比较完成后数据往后移动,下一个的preDiff就是上一次的curDiff
//不能将这行代码放到if外面,preDiff只有在坡度发生变化的时候才去更改,而不是每次都去更改,
//为了解决上方的第三点:单调平破
preDiff = curDiff;
}
}
return result;
}
public static void main(String[] args) {
// int[] arr = {1,2,2,3,4};
int[] arr = {1,17,5,10,13,15,10,5,16,8};
int result = getResult(arr);
System.out.println(result);
}