系列文章目录

第1章 专家系统
第2章 决策树
第3章 神经元和感知机
识别手写数字——感知机
第4章 线性回归
第5章 逻辑斯蒂回归和分类

---

前言

支持向量机(Support Vector Machine) 于1995年发表，由于其优越的性能和广泛的适用性，成为机器学习的主流技术，并成为解决一般性分类问题的首选方法之一。

支持向量机的发明来源于对分类器决策边界的考察。对于线性可分的两类数据点，有很多条不同的直线可以作为分类的决策边界。有的边界距离两侧或者某一侧的数据点比较近，而有的边界距离两侧的数据点都比较远。在这两种边界中，后者是更好的分类边界。它离所有样本点都更远，可以在两类数据点之间形成更宽的分隔带。样本点落在边界附近的概率相对较低，尤其是那些没有在训练样本集中出现过的未知数据点，这样的决策边界具有更优秀的泛化能力，更有可能对它们进行正确分类。反之，如果决策边界距离已知的训练样本很近，那么，数据点就有更大概率落在边界上或者边界附近，错误分类的概率就会大大增加，相应的泛化能力就会下降。因此，支持向量机的目标是寻找最宽的分隔带。

线性可分

下面是看浙大机器学习网课时所作的一点笔记。

支持向量机的优化问题

对于某个编号为$i$的样本点 $x_i$，线性分类器如何进行分类决策呢？下面我们把逻辑斯蒂回归或者感知机分类的过程用几何语言描述一下。如下图所示，取一个从原点发出的向量 $\omega$，使之垂直于决策边界。样本 $x_i$，也可以视作一个从原点发出的向量。那么，样本$x_i$属于哪个类别，或者说落在决策边界的哪一边，取决于它在$\omega$方向上的投影长度$\omega \cdot x_i/||\omega ||$。由于我们只关心投影的相对长度，因此，可以忽略向量$\omega$的长度$||\omega ||$，直接使用点积$\omega \cdot x_i$，然后选取常量$b$作为分割点，这样就得到了判别$x_i$类别的决策规则。
·当$\omega \cdot x_i+b\ge 0$时，$x_i$是正样本；
·当$\omega \cdot x_i+b<0$时，$x_i$是负样本。

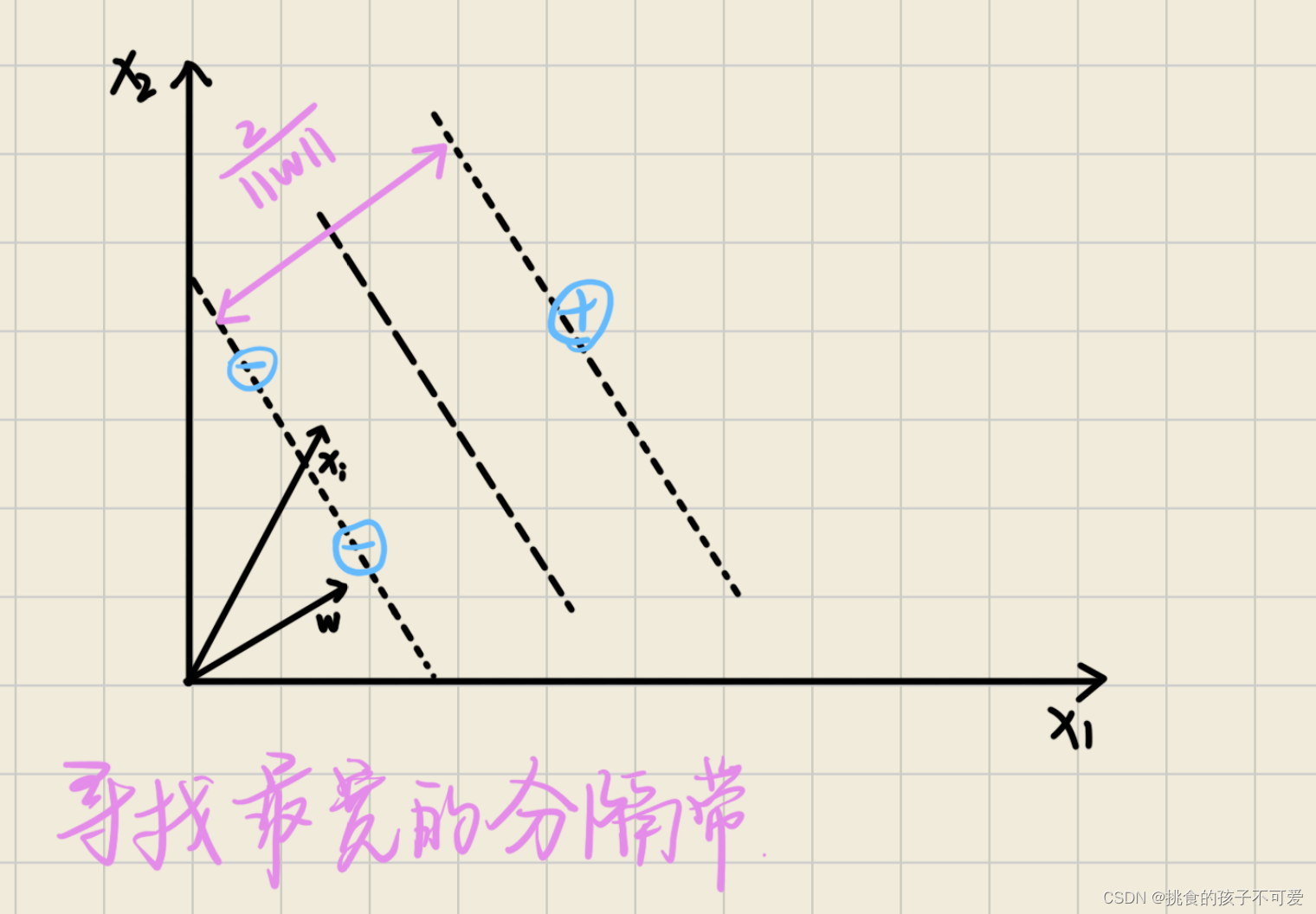
下面，给决策规则增加限制,使得决策边界有一定的宽度，而不是无宽度的直线。

·如果$x_i$是正样本，我们要求$\omega \cdot x_i+b\ge 1$
·如果$x_i$是负样本，我们要求$\omega \cdot x_i+b\le -1$
引入标记变量$y_i$,对于正样本$y_i=1$，对于负样本$y_i=-1$。
于是上面的规则可以改写为，对于任何样本$(x_i,y_i)$，$y_i(\omega \cdot x_i+b)-1\ge 0$
而对于落在分隔带边缘上的样本,$y_i(\omega \cdot x_i+b)-1=0$。我们称这些样本点为支持向量。
根据支持向量，我们还可以计算出分隔带的宽度。假设有一个正样本支持向量$x_{+}$，一个负样本支持向量$x_{-}$，分隔带的宽度就是这两个向量在$\omega$方向上的投影长度之差，即$2/||\omega ||$。
$$\begin{array}{rl}& \left({\mathbf{x}}_{+}-{\mathbf{x}}_{-}\right)\cdot \frac{\mathbf{w}}{\Vert \mathbf{w}\Vert }\\ =& \frac{(1-b)-(-1-b)}{\Vert \mathbf{w}\Vert }\\ =& \frac{2}{\Vert \mathbf{w}\Vert }\end{array}$$
支持向量机的目标是最大化分隔带的宽度，也就是最小化$\Vert \omega \Vert$,为了数学上计算方便，我们将目标设定为最小化$\frac{1}{2}{\Vert \omega \Vert }^2$。
这是一个带有约束条件的最优化问题。
约束条件是对于所有样本$y_i(\omega \cdot x_i+b)-1\ge 0$。对于有约束条件的最优化问题，需要采用拉格朗日乘子法。

拉格朗日乘子法

拉格朗日乘子法可以将有约束的最优化问题，转化为无约束的最优化问题。
假设要优化的目标函数是$f(x)$，对于有多个约束条件的情况，设第$i$个约束条件为$g(x{)}_i=0$（不等式约束的情况类似），可以最终转化为无约束优化$L(x,\alpha )=f(x)+{\sum }_i{\alpha }_i{g}_i(x)$。
支持向量机的优化目标：$\frac{1}{2}{\Vert \omega \Vert }^2$
约束条件不妨换成 $1-y_i(\omega \cdot x_i+b)\le 0$
根据拉格朗日乘子法，优化的目标变为最小化如下函数$L$:
$$L(\omega ,b,\alpha )=\frac{1}{2}{\Vert \omega \Vert }^2+\sum _i{\alpha }_i\left[1-y_i\left(\omega \cdot +b\right)\right]$$
支持向量机优化问题的KKT条件如下：
$$\{\begin{array}{l}{y}_i\left(\mathbf{w}\cdot {\mathbf{x}}_i+b\right)-1⩾0\\ {\alpha }_i⩾0\\ {\alpha }_i\left[y_i\left(\mathbf{w}\cdot {\mathbf{x}}_i+b\right)-1\right]=0\end{array}$$
观察这些条件，可以发现，只有当样本位于分隔带边缘时，才有$y_i(\omega \cdot x_i+b)-1=0$，这些样本就是支持向量。对于其他样本，$y_i(\omega \cdot x_i+b)-1>0$，也就是说，对于非支持向量，必须有${\alpha }_i=0$。因此，只有当$x_i$是支持向量的时候，才有${\alpha }_i\ne 0$。
支持向量机产生的模型仅与支持向量有关。
下面，对目标函数$L$求导数，令导数等于0,进行求解。
$$\begin{gathered} \frac{\partial L}{\partial \omega }=\omega -\sum _i{\alpha }_i{y}_i{x}_i=0 \\ \frac{\partial L}{\partial b}=-\sum _i{\alpha }_i{y}_i=0 \end{gathered}$$
即：
$$\begin{gathered} \omega =\sum _i{\alpha }_i{y}_i{x}_i \\ 0=\sum _i{\alpha }_i{y}_i \end{gathered}$$
将上面两个结果代入目标函数，从中消去$\omega$和$b$，得到下面新的目标函数。
$$L=\sum _i{\alpha }_i-\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_{\mathbf{i}}{\mathbf{x}}_{\mathbf{j}}$$
由于仅剩下变量$\alpha$，因此，这是一个二次规划问题，可以使用各种数值优化方法和通用的二次规划问题来解决它。
求解出$\alpha$后，就可以得到$\omega$和$b$，以及模型的分类判别函数。
$$\omega \cdot x+b=\sum _i{\alpha }_i\cdot y_i\cdot {\mathbf{x}}_{\mathbf{i}}\cdot x+b$$

非线性分类与核函数

如上所示，我们发现在支持向量机的目标函数以及产出的模型中，关于输入数据，只有向量内积运算$x_i\cdot x_j$。这个特点在处理非线性分类问题的时候非常有价值。
如何解决线性不可分的问题？

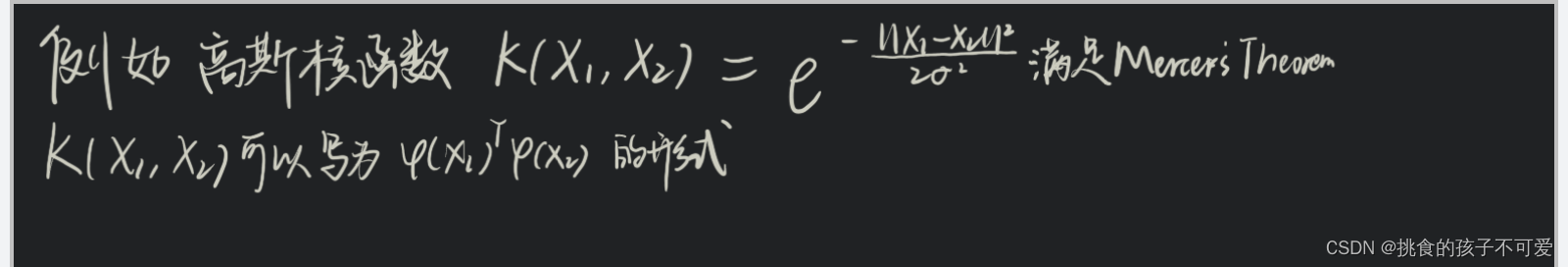
也就是说，面对在低维空间线性不可分的问题，通常可以采用将数据映射到高维空间的方法，这样问题就变成了高维空间的线性可分问题。例如上面手写笔记中的异或问题。异或问题在二维平面上线性不可分，但其实我们也可以直接增加一个维度，使得异或问题在三维空间中变成线性可分问题。
在二维平面上，无法找到一条直线将(0，0)(1，1)与(0，1)(1，0)分割在直线两侧。但我们增加一个维度，将两组点映射到(0，0，0)、(1，1，0)和(0，1，1)(1，0，1)时，两组点就可以用一个二维平面分隔开来。
实际问题的空间变换要比异或问题复杂得多。假设$x\to \varphi (x)$是我们需要的空间变换，我们要把所有数据经过$\varphi$变换，然后应用支持向量机。由于支持向量机的计算中只用到向量内积运算，因此只需要计算 $\varphi (x_i)\cdot \varphi (x_j)$。我们注意到，其实并不需要真的计算变换 ，真正需要的是一个关于两个向量的函数，我们把这个函数记作$\kappa$。
$$\kappa (x_i,x_j)=\varphi (x_i)\cdot \varphi (x_j)$$
我们把$\kappa$称作核函数，它为我们进行空间变换提供了很大便利，是解决非线性分类问题的关键。如果空间变换的形式是已知的，当然可以直接计算出函数 $\kappa$。然而，核函数的优势是我们通常并不需要知道空间变换的具体形式，只需要定义核函数如何计算即可。下面是一些常用的核函数。
·线性核：$\kappa (x_i,,x_j)=x_i\cdot x_j$，这就是支持向量机原始的线性形式。
·多项式核：$\kappa (x_i,,x_j)=(x_i\cdot x_j{)}^d$，其中d是多项式的次数。
·高斯核：$\kappa (x_i,,x_j)=exp(-{\Vert x_i-x_J\Vert }^2/2{\sigma }^2)$，其中$\sigma$是带宽参数，适用于高斯分布的数据。高斯核也叫作径向基函数（Radial Basis Function,RBF）核。核函数中的空间变换思想在其他模型中也很常见。比如，后面我们会看到多层感知机组织成的神经网络模型，实际上也可以理解为不断对数据进行空间变换，最终将数据映射为不同类别，或者映射到期望的目标输出。

支持向量机代码

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
'''
@Project ：demo1 
@File    ：SVM.py
@IDE     ：PyCharm 
@Author  ：Yue
@Date    ：2024-03-21 22:59 
'''
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm,datasets

# 加载鸢尾花数据集
iris = datasets.load_iris()
index = iris.target < 2
X = iris.data[index,:2]
Y = iris.target[index]

# 创建两个支持向量机
# C 是正则化参数,数值越大 正则化强度越小
# 正则化参数 是用来防止过拟合的
# 这里使用一个较大的参数值减弱正则化，以便显示原始结果
linear_svm = svm.SVC(kernel='linear', C=1e5)
# 高斯核的带宽参数是gamma
rbf_svm = svm.SVC(kernel='rbf', C=1e5, gamma=1)
svm_models = [linear_svm, rbf_svm]
for model in svm_models:
    model.fit(X,Y)

# 分别绘制两个支持向量机的决策边界
xx,yy = np.meshgrid(
    np.arange(X[:,0].min()-0.5 ,X[:,0].max()+0.5 ,0.1),
    np.arange(X[:,1].min()-0.5 ,X[:,1].max()+0.5 ,0.1),
)
input = np.concatenate(
    (xx.reshape((-1,1)) ,yy.reshape((-1,1)) ), axis=1
)
for model in svm_models:
    z = model.predict(input)
    z = z.reshape(xx.shape)
    fig = plt.pcolormesh(xx ,yy ,z ,cmap=plt.cm.Paired)
    # 绘制样本点
    for i in range(2):
        index = Y == i
        mark = 'kx' if i == 0 else 'k+'
        plt.plot(X[index,0] ,X[index,1], mark)
    # 绘制支持向量
    support = model.support_vectors_
    plt.scatter(support[:,0] ,support[:,1] , c='y', edgecolors='k')
    plt.show()

这段代码有几个点没有看懂，我是这么向ai提问的。

它的回答：
在这段代码中，z 是一个一维数组，包含了使用 SVM 模型对网格点 input 进行预测得到的结果。

然而，pcolormesh 函数需要一个二维数组作为 Z 参数，以便能够在每个 (xx, yy) 网格点上绘制颜色。为了将一维数组 z 转换为这样的二维数组，我们需要使用 reshape 方法。

reshape 方法的作用是重新排列数组中元素的布局，而不改变数组中的数据内容。在这个过程中，我们根据 xx 和 yy 的形状来定义 z 重塑后的形状。

于是，它变成了一个34*37的形状，也就是网格中的每个点，都对应了一个预测输出。

具体来说，xx 和 yy 是通过 np.meshgrid 函数生成的，这个函数会创建两个二维数组，其中 xx 包含所有水平网格线的 x 坐标值，yy 包含所有垂直网格线的 y 坐标值。xx 和 yy 的形状是相同的，并且都是由 input 数组的大小决定的。

这里是如何使用 reshape 方法的：

z = model.predict(input)
z = z.reshape(xx.shape)  # 将 z 重塑成与 xx 和 yy 相同的形状

在这个例子中，input 是一个二维数组，其形状是 (n_samples, 2)，其中 n_samples 是网格点的数量。reshape 方法将 z 从一个长度为 n_samples 的一维数组转换为一个形状为 (n_samples, 1) 的二维数组。然后，这个二维数组可以与 xx 和 yy 配合使用，因为 xx 和 yy 的形状是 (n_samples, n_samples)，其中 n_samples 是网格点的数量。
最终，z.reshape(xx.shape) 会得到一个形状为 (n_samples, n_samples) 的二维数组，其中每个元素对应于 (xx[i, j], yy[i, j]) 网格点的预测结果。这样，pcolormesh 函数就可以根据这个二维数组绘制出每个网格点的颜色，从而生成决策边界的图像。
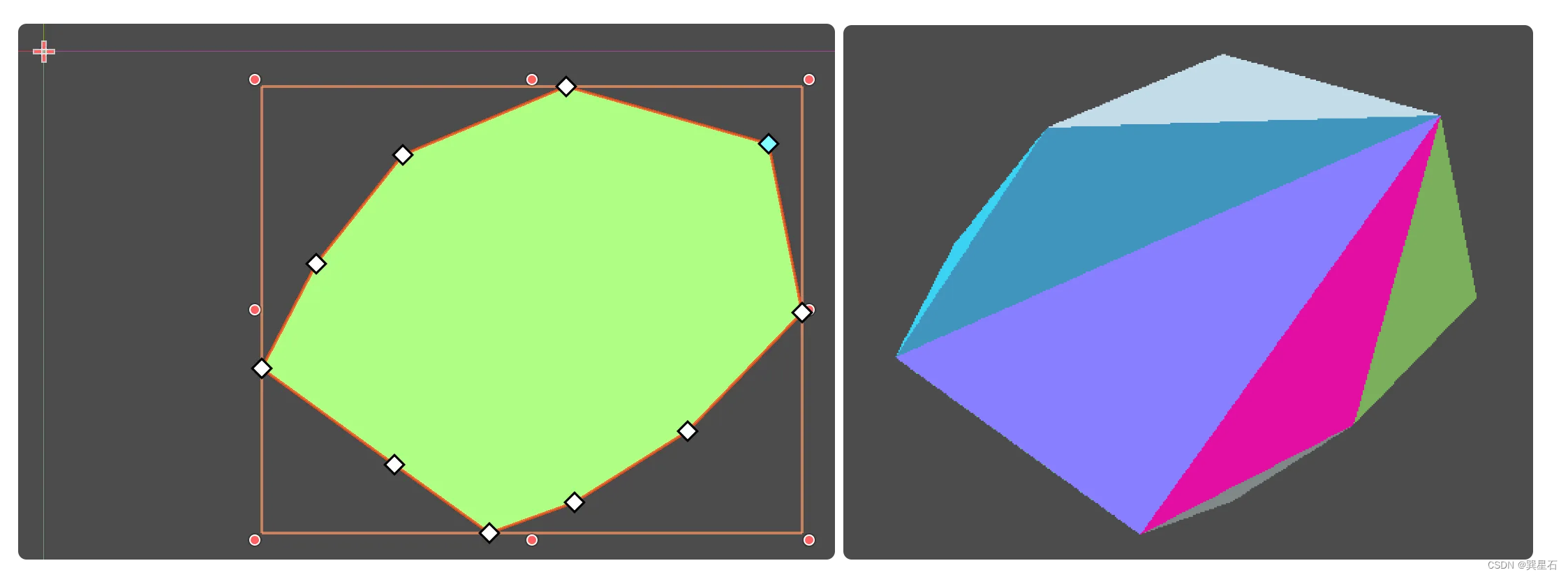
采用线性核的SVM：

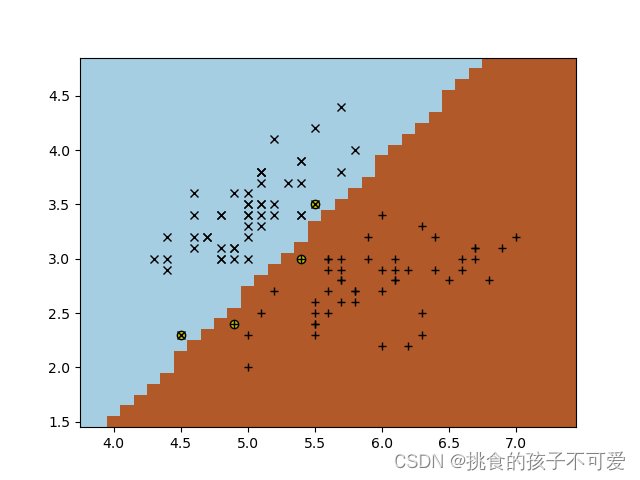
高斯核的SVM：

---

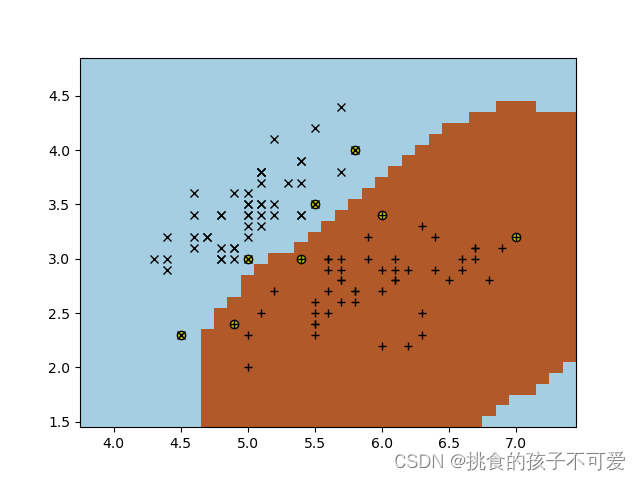
总结

`这部分主要介绍了支持向量机的分类模型，中间涉及了很多概念，什么是线性可分，支持向量机的优化目标，如何将分类问题转化为优化问题，如何求解这个优化问题，求解过程中又引入了核函数的概念。
要记住的是，面对低维空间线性不可分的问题，采用将数据映射到高维空间的思想，支持向量机是这一思想的代表方法。

感谢阅读，敬请评论区批评指正哦