[数据结构]堆

news2024/9/21 14:33:44

一、堆是什么？

堆是一种完全二叉树

完全二叉树的定义：完全二叉树的形式是指除了最后一层之外，其他所有层的结点都是满的，而最后一层的所有结点都靠左边。​​​​​​，从左到右连续。

教材上定义如下:

若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

二、堆

堆分为大堆和小堆

大堆：对于任意一个父结点来说，其子结点的值都小于这个父节点。也就是（父亲>儿子）

小堆:   对于任意一个父结点来说，其子结点的值都大于这个父节点。也就是（父亲<儿子）

所以对堆插入数据时,我们要调整堆,我们可能会发现,导入数据后会出现一种特殊的现象,父子的位置互换了,父亲成为了儿子,儿子成为了父亲,甚至可能影响了祖先。

父子存储关系：

leftchild=parent*2+1

rightchild=parent*2+2

parent=(child-1)/2

三、堆的调整

1.向上调整

字面意思从下往上进行数据的调整，举个例子，假设我这里有个小堆：

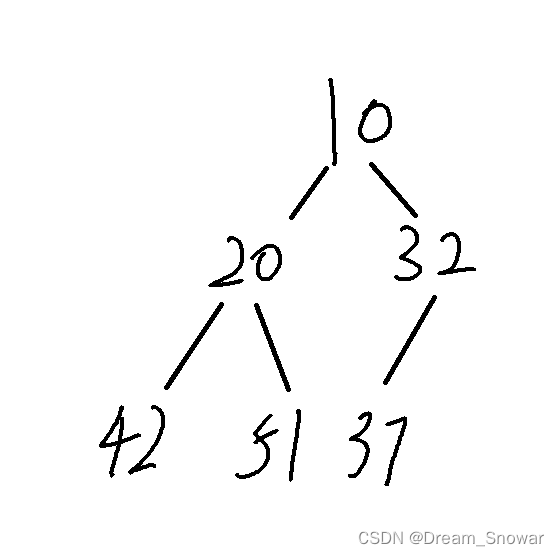
假设我们这里在堆插入一个60：

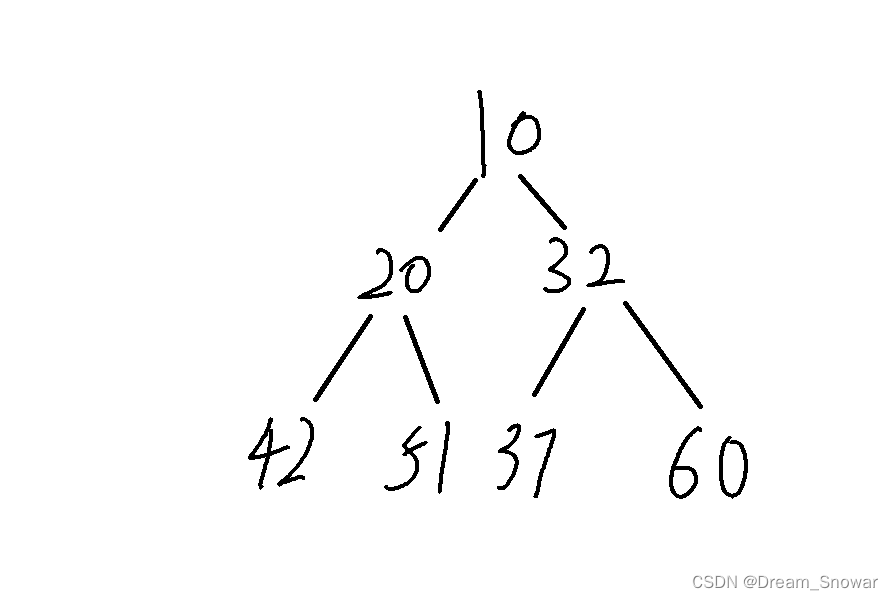
我们会发现符合小堆的定义。

那么，我们要是插入一个30呢？

我们根据小堆的定义我们需要把30与32 的位置对调，如上图。

那么，如果我们插入的是5呢？

我们会发现5比32小，他们的位置交换，5比10还小，所以5和10的位置也交换，过程如上图。

最后这个堆就是这样的：

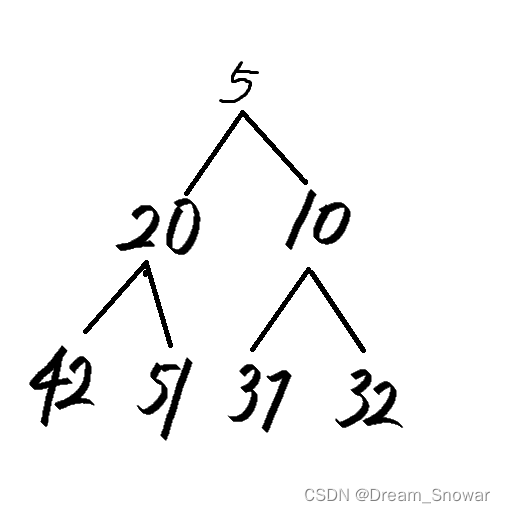
下面是代码实现：

typedef int HPDataType;//定义堆的数据类型
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}Heap;//堆
void Adjustup(HPDataType* a, HPDataType child)//传入堆的指针和孩子的下标
{
	int parent = (child - 1) / 2;//通过公式算出父亲的下标
	while (child > 0)//设计循环条件,因本质为数组,所以下标大于0,且孩子下标如果是0,则孩子为祖先
	{
		if (a[child] < a[parent])//判断父与子大小
		{
			swap(&a[child], &a[parent]);//交换父子的位置的值
			child = parent;//求出此时交换后原来孩子的下标,便于与新父亲比较
			parent = (parent - 1) / 2;//通过新的儿子的下标求出父亲的下标,便于下一次判断
		}
		else
		{
			break;//退出
		}
	}
}
void swap(HPDataType* a, HPDataType* b)//交换数值的函数
{
	HPDataType tmp = *a;
	*a = *b;
	*b = tmp;
}

2.向下调整

字面意思，就是从上到下调整，这时有人说这样插入新数值时，用这个好麻烦啊，确实是这样的，向下调整，我们一般可以用于已经存在的数组来建堆。

下面我们来举个例子，我们拥有以下数组：

{50，100，23，45，67，77}，我们要把他们建立成小堆

建立成堆的逻辑结构：

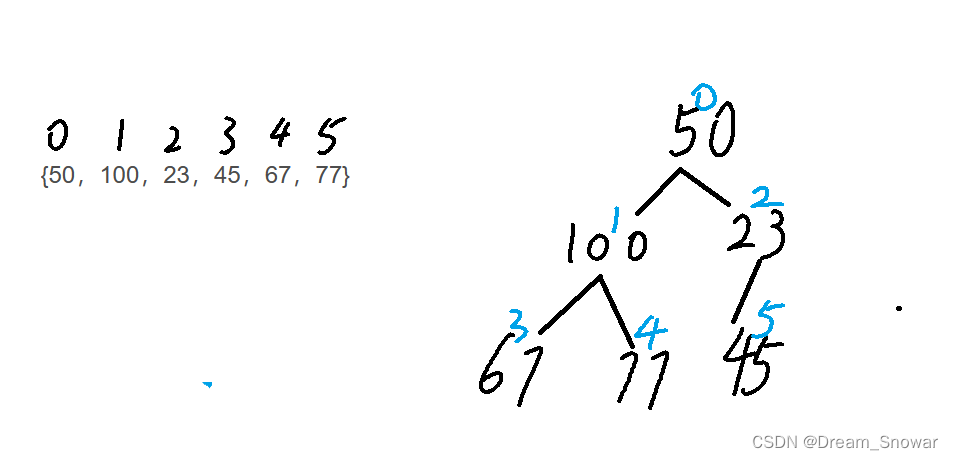
我们从50开始对其判断

看到这里，可能会有疑惑，为什么100>77同时100>67,交换的是100和67，因为如果77和100交换之后继续比较我们会发现67<77，所以上图是对的

因此我们可以得到的堆最后、如下：

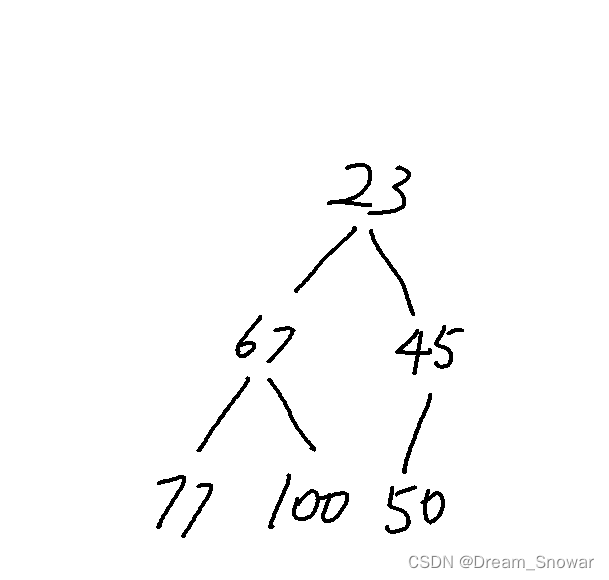
思考一下这样对吗？

下面我们来用代码实现：

//建立堆,堆的数据类型,交换数值函数省略
void Adjustdown(HPDataType* a, int n, int parent)//传入堆中位置的指针,传入堆的最后一位下标和开
{                                                //始的父亲下标
	int child = parent * 2 + 1;//算出孩子下标
	while (child < n)//构建循环条件
	{
		if (child + 1 < n && a[child + 1] < a[child])//如果孩子没到最后同时右孩子小于左孩子
		{
			++child;//最小的孩子为右孩子
		}
		if (a[child] < a[parent])//孩子和父亲比较
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

将这些搞懂了,我们就能尝试去手搓一个堆了

四、手搓堆

 知道这些我们可以尝试自己来手搓一个堆了，假设我们来手搓一个大堆，顺便实现相应的操作。

1.堆的结构体和数据类型

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}Heap;

2.堆的初始化

void HeapInit(Heap* hp)
{
	assert(hp);
	hp->a = NULL;
	hp->capacity = 0;
	hp->size = 0;
}

3.对堆的空间判断和扩容

我们知道堆的物理结构数组，我们可以联想到顺序表，我们需要动态开辟空间，所以需要在插入新数据时，对现有的空间进行判断。

void AddHeap(Heap* hp)
{
	int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
	HPDataType* temp = realloc(hp->a, sizeof(HPDataType) * newcapacity);
	if (temp==NULL)
	{
		perror("realloc fail");
		return;
	}
	hp->a = temp;
	hp->capacity = newcapacity;
}

4.在堆尾部插入数据

如果我们在队尾差尾一个数据，根据对的定义我们需要建堆进行调整，前面我们说过这里适合用向上调整。

void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	if(hp->size==hp->capacity)
	{
		AddHeap(hp);
	}
	hp->a[hp->size] = x;
	hp->size++;
	Adjustup(hp->a, hp->size - 1);
}

void Adjustup(HPDataType* a, HPDataType child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

5.在堆头删除数据

删除堆头数据一样会使本来的关系改变，所以我们需要堆数据的位置进行调整，因为我们改变的时头，所以我们这里使用向下调整比较好。

void Adjustup(HPDataType* a, HPDataType child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapPop(Heap* hp)
{
	assert(hp);
	assert(hp->a);
	swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;
	Adjustdown(hp->a, hp->size, 0);
}

6.获取堆顶的数据，判断是否为空，获取数据个数

这个比较简单我直接上代码了

HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->a);
	return hp->a[0];
}
int HeapSize(Heap* hp)
{
	assert(hp);
	return hp->size;
}
int HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->size == 0;
}

7.堆的销毁

动态内存开辟的空间要释放

void HeapDestory(Heap* hp)
{
	assert(hp);
	free(hp->a);
	hp->a = NULL;
	hp->capacity = 0;
	hp->size = 0;
}

8.总体代码

//Heap.h

#pragma once
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}Heap;

//堆的初始化
void HeapInit(Heap* hp);
// 堆的构建
//void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
//Heap.c

#include"Heap.h"
void HeapInit(Heap* hp)
{
	assert(hp);
	hp->a = NULL;
	hp->capacity = 0;
	hp->size = 0;
}
void AddHeap(Heap* hp)
{
	int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
	HPDataType* temp = realloc(hp->a, sizeof(HPDataType) * newcapacity);
	if (temp==NULL)
	{
		perror("realloc fail");
		return;
	}
	hp->a = temp;
	hp->capacity = newcapacity;
}
void HeapDestory(Heap* hp)
{
	assert(hp);
	free(hp->a);
	hp->a = NULL;
	hp->capacity = 0;
	hp->size = 0;
}
void swap(HPDataType* a, HPDataType* b)
{
	HPDataType tmp = *a;
	*a = *b;
	*b = tmp;
}

void Adjustup(HPDataType* a, HPDataType child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void Adjustdown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			++child;
		}
		if (a[child] > a[parent])
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	if(hp->size==hp->capacity)
	{
		AddHeap(hp);
	}
	hp->a[hp->size] = x;
	hp->size++;
	Adjustup(hp->a, hp->size - 1);
}
void HeapPop(Heap* hp)
{
	assert(hp);
	assert(hp->a);
	swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;
	Adjustdown(hp->a, hp->size, 0);
}
HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->a);
	return hp->a[0];
}
int HeapSize(Heap* hp)
{
	assert(hp);
	return hp->size;
}
int HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->size == 0;
}

最后我们来测试一下这些功能

//test.c


#include<stdio.h>
#include"Heap.h"
int main()
{
	int a[] = { 50,100,70,65,60,32 };
	Heap hp;
	HeapInit(&hp);
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		HeapPush(&hp, a[i]);
	}

	while (!HeapEmpty(&hp))
	{
		printf("%d\n", HeapTop(&hp));
		HeapPop(&hp);
	}
	HeapDestory(&hp);
	return 0;
}

感谢阅读!

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1537080.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

纹波和噪声有啥区别（一）

纹波和噪声有啥区别（一）

首先要知道的是他们都是在电源输出中出现的信号波动&#xff0c;但两者存在明显的区别。 一&#xff0c;纹波的产生 电源纹波是指电源输出时&#xff0c;叠加在稳定的直流电源上的交流成分。 这种波动主要是由于电源自身的开关、PWM 调节等因素引起的&#xff0c;其频率一般…
阅读更多...
Javaweb的学习21_CSS_属性

Javaweb的学习21_CSS_属性

CSS的属性 (常用)属性&#xff1a; 1. 字体、文本 font-size&#xff1a;字体大小 color&#xff1a;文本颜色 text-align&#xff1a;文本的对齐方式 line-height&#xff1a;行高 2. 背景 background&#xff1a;是个复合属性 3. 边框 border&#xff1a;设置边框&#xff0c…
阅读更多...
1升级powershell后才能安装WSL2--最后安装linux--Ubuntu 22.04.3 LTS

1升级powershell后才能安装WSL2--最后安装linux--Ubuntu 22.04.3 LTS

视频 https://www.bilibili.com/video/BV1uH4y1W7UX查看电脑本版 步骤1:使用 Winget 方式安装 PowerShell 查看是否能更新PowerShell– winget search Microsoft.PowerShell查看结果为 名称 ID 版本 源 ----------------------------…
阅读更多...
HTML小游戏27 - Chuck Chicken 魔法蛋网页游戏（附完整源码）

HTML小游戏27 - Chuck Chicken 魔法蛋网页游戏（附完整源码）

&#x1f482; 网站推荐:【神级源码资源网】【摸鱼小游戏】 【工具大全】&#x1f91f; 基于Web端打造的&#xff1a;&#x1f449;【轻量化工具创作平台】&#x1f485; 想寻找共同学习交流、摸鱼划水的小伙伴&#xff0c;请点击【学习交流群】 本节教程我会带大家使用 HTML 、…
阅读更多...
【Kafka系列】Kafka事务一般在什么场景下使用呢

【Kafka系列】Kafka事务一般在什么场景下使用呢

面试官&#xff1a;听说你精通Kafka&#xff0c;那我就考考你吧 面试官&#xff1a;不用慌尽管说&#xff0c;错了也没关系&#x1f60a;。。。 以【面试官面试】的形式来分享技术&#xff0c;本期是《Kafka系列》&#xff0c;感兴趣就关注我吧❤️ 面试官&#xff1a;生产者重…
阅读更多...
G1和ZGC垃圾回收器学习

G1和ZGC垃圾回收器学习

前言 ​ 随着JDK17的占有率不断升高和SpringBoot3最低支持JDk17&#xff0c;JDK17很大概率会成为大家后续升级的一个选择&#xff0c;而JDK17上最重要的垃圾回收器G1和ZGC&#xff0c;也就显得格外重要。大家提前了解或者学习一下肯定是有用的。 ​ 本篇文章也默认大家了解一…
阅读更多...
【linux】进程地址空间（进程三）

【linux】进程地址空间（进程三）

目录 快速了解&#xff1a;引入最基本的理解&#xff1a;细节&#xff1a;如何理解地址空间&#xff1a;a.什么是划分区域&#xff1a;b.地址空间的理解&#xff1a; 为什么要有进程空间&#xff1f;进一步理解页表与写时拷贝&#xff1a; 快速了解&#xff1a; 先来看这样一段…
阅读更多...
docker入门（九）—— docker网络详细介绍

docker入门（九）—— docker网络详细介绍

docker 网络 准备工作&#xff1a;清空所有镜像和容器 docker rm -f $(docker ps -aq) docker rmi -f $(docker images -aq)docker0 网络 查看本地网络 ip addr[rootiZbp15293q8kgzhur7n6kvZ /]# ip addr# 本地回环网络 1: lo: <LOOPBACK,UP,LOWER_UP> mtu 65536 qdisc…
阅读更多...
jmeter接口导入方式

jmeter接口导入方式

curl直接导入 1、操作页面后&#xff0c;F12查看接口&#xff0c;右击接口-copy-copy as cURL 2、jmeter 工具-import from cURL&#xff0c;粘贴上面复制的curl 根据接口文档导入 1、接口文档示例如下&#xff1a; Path&#xff1a; /api/jobs/xps/exec Method&#xf…
阅读更多...
3d画线生成模型之后最大化找不到---模大狮模型网

3d画线生成模型之后最大化找不到---模大狮模型网

当你在3D建模软件中画线生成模型后&#xff0c;如果最大化找不到该模型&#xff0c;可能是因为以下几种情况导致&#xff1a; 模型位置偏移&#xff1a; 可能你在绘制线条时&#xff0c;将模型画在了视图界面之外&#xff0c;导致最大化时无法看到。尝试平移或旋转模型&#x…
阅读更多...
东方博宜 1449. 求满足条件的数的和

东方博宜 1449. 求满足条件的数的和

东方博宜 1449. 求满足条件的数的和 这道题我苦想了很久&#xff0c;觉得2个及2个以上很难解决&#xff0c;但是后面发现&#xff0c;可以用一个变量记录次数&#xff0c;次数大于等于2就好了。 #include<iostream> using namespace std; int main() {int n ;cin >…
阅读更多...
企业用大模型如何更具「效价比」？百度智能云发布5款大模型新品

企业用大模型如何更具「效价比」？百度智能云发布5款大模型新品

服务8万企业用户&#xff0c;累计帮助用户精调1.3万个大模型&#xff0c;帮助用户开发出16万个大模型应用&#xff0c;自2023年12月以来百度智能云千帆大模型平台API日调用量环比增长97%...从一年前国内大模型平台的“开路先锋”到如今的大模型“超级工厂”&#xff0c;百度智能…
阅读更多...
革新水库大坝监测：传统软件与云平台之比较

革新水库大坝监测：传统软件与云平台之比较

在水库大坝的监测管理领域&#xff0c;传统监测软件虽然曾发挥了重要作用&#xff0c;但在多方面显示出了其局限性。传统解决方案通常伴随着高昂的运维成本&#xff0c;需要大量的硬件支持和人员维护&#xff0c;且软件整合和升级困难&#xff0c;限制了其灵活性和扩展性。 点击…
阅读更多...
类对象的初始化过程与方法

类对象的初始化过程与方法

类初始化过程与方法 一、类对象的初始化过程 1.初始化的过程 &#xff08;1&#xff09;对象在实例化的时候需要调用构造函数&#xff0c;如果对应的构造函数调用不了&#xff0c;这个对象是没有办法实例化的。 &#xff08;2&#xff09;构造函数的执行&#xff0c;是在内…
阅读更多...
好看的表情壁纸

好看的表情壁纸

不定时更新表情壁纸&#xff0c;后期支持头像&#xff0c;wx背景等&#xff0c;个人开发&#xff0c;觉得不错&#xff0c;可前往小程序或者公众号查看
阅读更多...
深入理解模板进阶：掌握C++模板的高级技巧

深入理解模板进阶：掌握C++模板的高级技巧

&#x1f389;个人名片&#xff1a; &#x1f43c;作者简介&#xff1a;一名乐于分享在学习道路上收获的大二在校生 &#x1f648;个人主页&#x1f389;&#xff1a;GOTXX &#x1f43c;个人WeChat&#xff1a;ILXOXVJE &#x1f43c;本文由GOTXX原创&#xff0c;首发CSDN&…
阅读更多...
基于springboot的员工绩效考核管理系统(含源文件)

基于springboot的员工绩效考核管理系统(含源文件)

&#xff08;源码附文章底部&#xff09; 摘 要 科学时代的发展改变了人类的生活&#xff0c;促使网络与计算机技术深入人类的各个角落&#xff0c;得以普及到人类的具体生活中&#xff0c;为人类的时代文明掀开新的篇章。本系统为月度员工绩效考核管理系统&#xff0c;是专为…
阅读更多...
JAVA入门第一步2.0

JAVA入门第一步2.0

一、JAVA中的关键字 Java中的关键字是Java编程语言中预先定义并保留的单词&#xff0c;它们具有特殊的含义&#xff0c;不能用作变量名、方法名或类名等标识符。以下是我查到的Java中的一些主要关键字&#xff1a; 由于我还在入门&#xff0c;所以所接触的关键字不多&#xf…
阅读更多...
从0到1实现RPC | 02 RpcConsumer的远程调用

从0到1实现RPC | 02 RpcConsumer的远程调用

一、RPC的简化版原理如下图&#xff08;核心是代理机制&#xff09;。 1.本地代理存根: Stub 2.本地序列化反序列化 3.网络通信 4.远程序列化反序列化 5.远程服务存根: Skeleton 6.调用实际业务服务 7.原路返回服务结果 8.返回给本地调用方 二、新建一个模块rpc-demo-c…
阅读更多...
如何真正改变自己？ 《掌控习惯》

如何真正改变自己？ 《掌控习惯》

维持改变 1.心态 目标与体系&#xff0c;谁是真正通往成功的钥匙&#xff1f; 2.行动 习惯转变的3个层次 身份 你要成为谁&#xff1f; 你为成为他而幸福吗&#xff1f;过程结果 习惯的基本原理&#xff1a;要重视微小的改变 维持改变成两个方面入手 一、心态&#xff1a;忽略…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023