目录

1  什么是堆排序

1.1  什么是堆

1.2  如何构建堆

1.3  举例说明

2  215. 数组中的第 K 个最大元素

2.1  子树大根化

2.2  遍历所有子树

2.3  弹出栈顶元素

2.4  完整代码

---

菜鸟做题，语言是 C++

1  什么是堆排序

1.1  什么是堆

堆的定义和分类：

• 堆是一棵完全二叉树
• 分为：大根堆、小根堆

堆的特点：

• 大根堆：在任一子树中，根节点都比左、右子节点大
• 小根堆：在任一子树中，根节点都比左、右子节点小

这就是为什么它叫 “大根” 堆或者 “小根” 堆吧？

1.2  如何构建堆

假设给定数组 [3，2，1，5，6，4]，要求我们把它构建为一个大根堆。

首先，我们可以把它想象成完全二叉树层序遍历的结果：

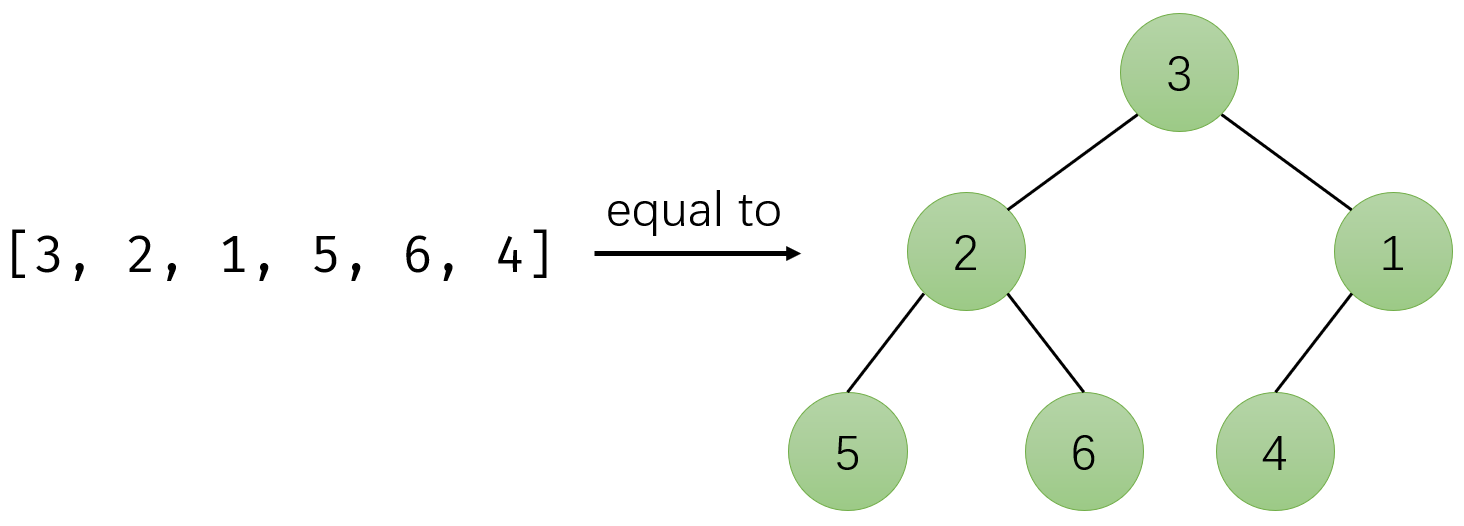
注意：这里我说的是 “想象成”！因为到时候我们直接处理数组就行了，不需要构建一个二叉树出来。

接着，既然在大根堆的任一子树中，根节点都比左、右子节点大，那么我们只需要遍历上述二叉树的每棵子树，然后让根节点最大即可。具体来说，如果 左、右子节点中的较大者 比根节点大，那么就让它和根节点交换位置。

代码实现交换用的就是一个 swap() 函数。

1.3  举例说明

如图 1 所示，我们从二叉树的最后一棵子树开始遍历（黄色部分）。由于根节点 “1” 比左子节点 “4” 小，因此让它们交换位置（红圈部分）：

为什么要从最后一棵子树开始遍历，从第一棵开始不行吗？答：到时候我们要处理受到影响的子树，“根据根节点找左或右子节点” 貌似要比 “根据左或右子节点找根节点” 容易。

如图 2 所示，我们接着遍历下一棵子树（黄色部分）。由于根节点 “2” 比右子节点 “6” 小（即左、右子节点中的较大者），因此让它们交换位置（红圈部分）：

如图 3 所示，我们继续遍历下一棵子树（黄色部分）。由于根节点 “3” 比左子节点 “6” 小（即左、右子节点中的较大者），因此让它们交换位置（红圈部分）：

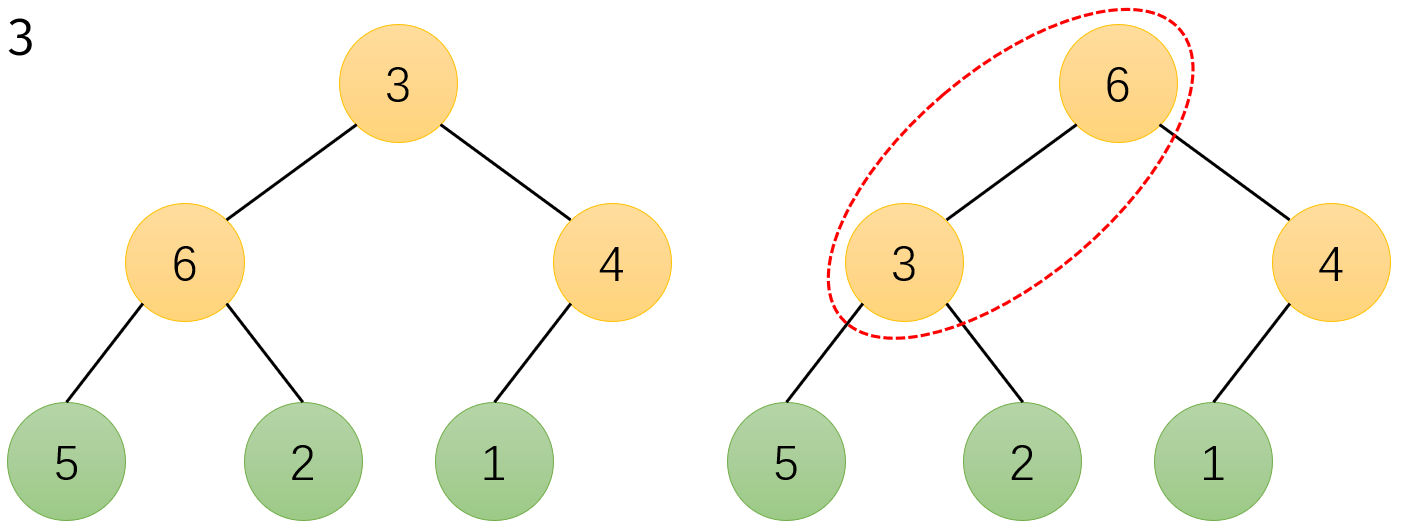
注意！这里完成交换以后，“3” 被换入了左下角子树中，使得该子树的根节点不再是最大值，因此我们需要重新处理左下角子树！如图 4 蓝色和红圈部分所示：

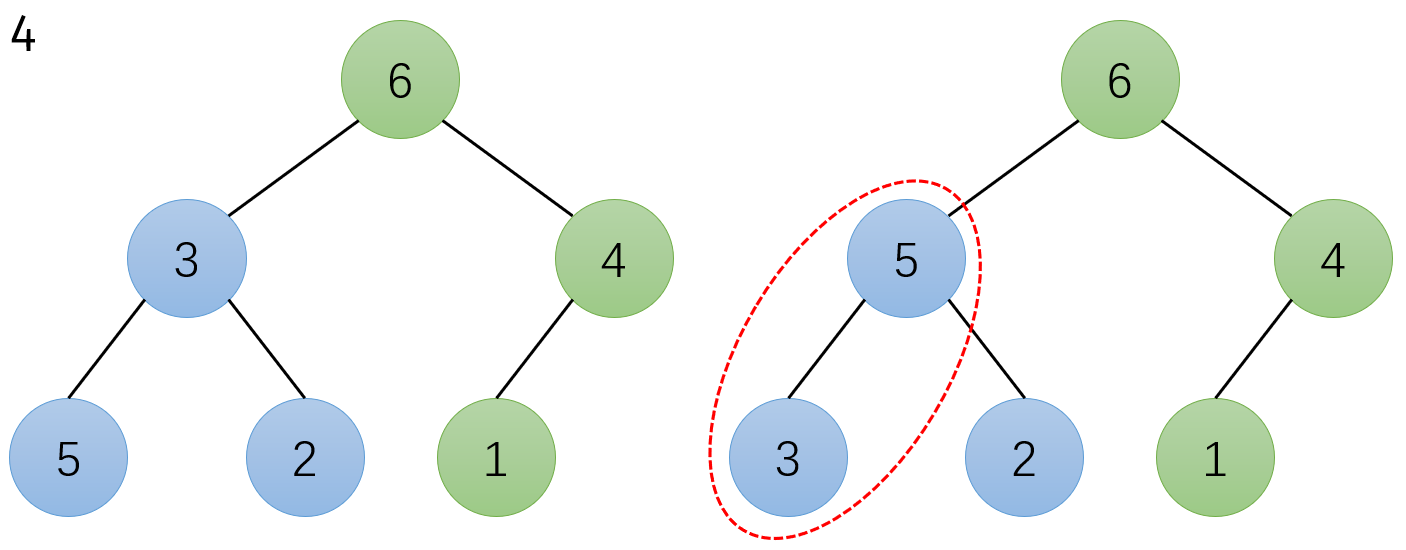
事实上，只要左右子节点不是叶节点，那么发生交换之后一定要重新处理受到影响的子树。

2  215. 数组中的第 K 个最大元素

构建堆 → 弹出堆顶 → 调整堆 → 弹出堆顶 → 调整堆

由于大根堆堆顶元素的值最大，即二叉树根节点的值最大，因此只要我们不断地弹出 堆顶元素 + 调整大根堆，就能依次得到第 xxx 大的元素。

Q：大根堆的本质不是数组吗？如何实现堆顶元素（即第 0 个元素）的弹出？

A：将堆顶元素（即第 0 个元素）与最后一个元素交换，并且人为让数组长度减一。

由于将堆顶元素移到了最后且令数组长度减一，那么调整大根堆时就不会再遍历到该堆顶元素了。

2.1  子树大根化

功能：完成对一棵子树的处理。

子树大根化的函数如下，代码逻辑为：

1. 获取左、右子节点的位置（说明见后文）
2. 根节点分别与左、右子节点比大小
3. 若根节点小于左、右子节点，则交换位置
4. 递归处理受到影响的左或右子树

再次强调，根节点只会和左、右子节点中的较大者交换位置。同时，如果此次交换涉及到的是左子节点，那么只需要递归处理受到影响的左子树，而没有必要处理右子树。

void maxHeapify(vector<int> & nums, int root, int heapSize) {
    // 获取左、右子节点位置
    int left = root * 2 + 1, right = root * 2 + 2;
    int largest = root;

    // 与左子节点比较
    if (left < heapSize && nums[left] > nums[largest]) {
        largest = left;
    }
    // 与右子节点比较
    if (right < heapSize && nums[right] > nums[largest]) {
        largest = right;
    }

    // 处理
    if (largest != root) {
        swap(nums[largest], nums[root]);
        maxHeapify(nums, largest, heapSize);
    }
}

说明： 为什么左、右子节点的位置是这样获取的？

int left = root * 2 + 1, right = root * 2 + 2;

因为完全二叉树有一个结论：如果根节点是第 i 个节点，那么它的左子节点是第 2i 个节点，右子节点是第 2i + 1 个节点（从 1 开始计数）。如下图所示：

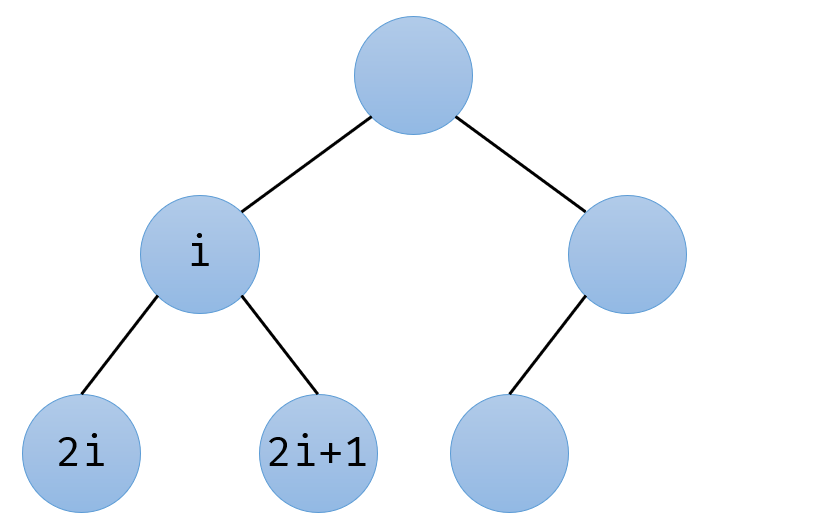
本质就是等比数列罢了。

2.2  遍历所有子树

使用 for 循环遍历所有子树，同时进行子树大根化：

void buildMaxHeap(vector<int> & nums, int heapSize) {
    for (int root = heapSize / 2; root >= 0; --root) {
        maxHeapify(nums, root, heapSize);
    } 
}

说明：为什么 root 是从 heapSize / 2 开始的？

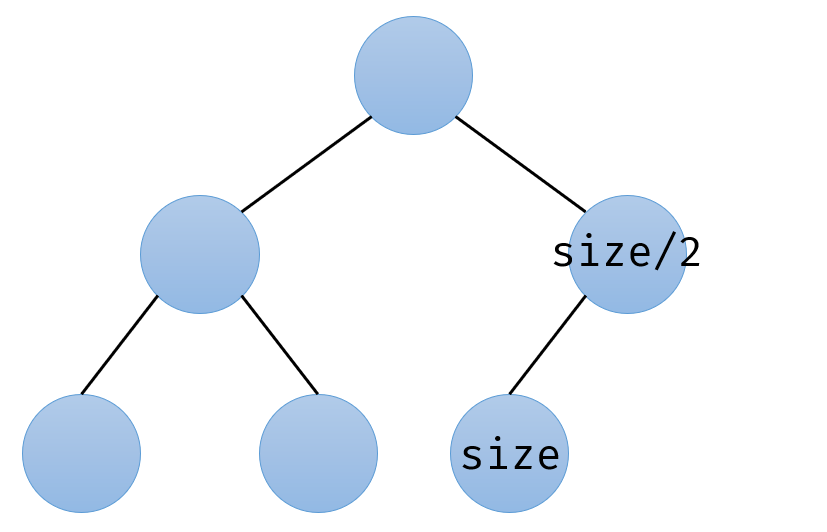
假设 size 是二叉树节点的总数，那么最后一个节点显然是第 size 个节点（从 1 开始计数）。最后一个节点所属的子树是最后一棵子树，即我们的遍历起点。再根据前文介绍，易得该子树的根节点是第 size / 2 个节点。因此，root 应该从 size / 2 开始。

这里的 size 就是指 heapSize，没有写 heapSize 是因为写不下了。

2.3  弹出栈顶元素

代码如下：

for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) {
    swap(nums[0], nums[i]); // 交换栈顶和最后一个元素
    --heapSize; // 人为让数组长度减一
    maxHeapify(nums, 0, heapSize); // 调整大根堆
}

由于我们寻找的是第 K 个最大元素，因此循环条件是 i >= nums.size() - k + 1，即循环 k 次。同时，由于弹出栈顶操作主要影响的是第 0 棵子树，因此只需要 maxHeapify(nums, 0, heapSize)，而不是重新构建大根堆。

2.4  完整代码

class Solution {
public:
    void maxHeapify(vector<int> & nums, int root, int heapSize) {
        int left = root * 2 + 1, right = root * 2 + 2;
        int largest = root;

        if (left < heapSize && nums[left] > nums[largest]) {
            largest = left;
        }
        if (right < heapSize && nums[right] > nums[largest]) {
            largest = right;
        }

        if (largest != root) {
            swap(nums[largest], nums[root]);
            maxHeapify(nums, largest, heapSize);
        }
    }

    void buildMaxHeap(vector<int> & nums, int heapSize) {
        for (int root = heapSize / 2; root >= 0; --root) {
            maxHeapify(nums, root, heapSize);
        } 
    }

    int findKthLargest(vector<int> & nums, int k) {
        int heapSize = nums.size();
        buildMaxHeap(nums, heapSize);

        for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) {
            swap(nums[0], nums[i]);
            --heapSize;
            maxHeapify(nums, 0, heapSize);
        }

        return nums[0];
    }
};

---

堆排序到底是谁想出来的，可恶 (〃＞皿＜)