光场显微粒子图像测速技术通过单光场相机即可实现微尺度三维速度场的测量,但单光场相机角度信息有限,导致粒子重建的轴向分辨率低、重建速度慢。基于此,提出一种基于卷积神经网络深度学习模型的光场显微粒子三维空间分布重建方法,以实现粒子三维分布的高分辨率快速重建。首先,根据光场显微成像模型,基于粒子的实际发光特性生成模拟光场图像,进而构建“粒子空间分布-光场图像”数据集;然后,耦合光场显微成像特点,建立卷积神经网络深度学习模型,通过“粒子空间分布-光场图像”数据集对模型进行学习和训练,获得光场显微三维粒子空间分布预测模型,并对预测模型的性能进行评价;最后,测量水平微通道层流流动中的示踪粒子空间分布和三维速度场。模拟和实验结果表明:相比常规的反卷积方法,所提方法的粒子重建轴向分辨率提高79.3%,基本消除了粒子重建的拉伸效应;单张图像重建时间仅为0.243s,可以满足实时测量的需求。
关键词:图像重建技术;微尺度流动;深度学习;三维粒子场;光场显微粒子图像测速技术
1引言
微流控芯片技术作为操纵微量流体的新兴技术[1],可将样品制备、反应、检测等基本操作单元集成到一块微米尺度芯片上,具有分辨率高、灵敏度高、成本低、分析速度快等优点,被广泛应用于生物、医学、化学、流体等领域[2-4]。由于微流控芯片流动通道尺寸微小,粘性力和表面张力对流动的影响不能忽视,微尺度流动比宏观流动更为复杂[5-6]。速度场是反映流动状态的重要参数,准确、高效的三维速度场测量是微尺度流动特性研究的重要基础。目前,粒子图像测速技术(PIV)[7]凭借精度高、分辨率高以及对流场干扰少等优势,被广泛应用于速度场测量中。目前,三维显微粒子图像测速技术(3DMicro-PIV)已经成为微流动三维速度场测量的主流方式,主要包括共聚焦扫描Micro-PIV技术[8]、体视Micro-PIV技术[9]、散焦Micro-PIV技术[10]和光场Micro-PIV技术[11-12]等。其中,光场Micro-PIV技术通过单光场相机[13-14]在单帧单曝光下可同时记录测量体内示踪粒子的深度和横向位置信息,进而实现微尺度三维速度场的测量,具有系统简单和时间分辨率高的优点,已成为微流动三维速度场测量技术研究热点之一[15-17]。
光场Micro-PIV技术通过光场图像记录示踪粒子的空间分布信息后,需进行粒子空间分布三维重建结合互相关算法计算三维速度场,故示踪粒子空间分布的三维重建是实现微尺度三维速度场测量的关键环节。现有的光场显微三维粒子空间分布重建方法包括重聚焦[18]、反卷积[12]、深度学习[19-20]等。重聚焦技术是基于几 何光学的示踪粒子三维重建技术,由于此方法忽略了显微镜的衍射效应,且光线采样密度受到微透镜间距(通常在100μm量级)的限制,其重建示踪粒子的横向分辨率和轴向定位精度较低。为提升粒子空间分布的重建分辨率,Song等[12]将基于波动光学的反卷积重建算法(LFD)引入光场Micro-PIV技术中,采用基于点扩散函数的Richardson-Lucy迭代算法[12,21-22]进行反演计算。但由于点扩散函数不满足平移不变性[23-24],反卷积算法 需要进行多次迭代计算,重建速度慢。此外,由于成像系统收光角度有限,采集的光场图像角度信息不足,粒子重建的轴向拉伸现象明显,轴向分辨率低。
近年来,将深度学习用于光场显微三维重建技术的研究已引起越来越多的关注[19-20,25]。Wagner等[19]提出一种基于深度学习的光场显微图像重建方法,该方法采用光场显微镜和平面照明显微镜通过实验分别获取光场图像和对应的三维体空间分布,从而实现深度学习数据集的构建,并构建卷积神经网络模型实现了生物影像的三维重建,其轴向重建分辨率可达(7.1±1.3)μm。Wang等[20]将视图通道深度(VCD)神经网络与光场显微镜结合,通过重聚焦扫描显微镜拍摄静态生物样本构建数据集,并利用视图通道深度神经网络模型实现动态样本的三维图像重建,取得了较好的重建效果。深度学习通过学习大量数据集并提取特征,从而实现对未学习样本的预测,因此,数据集样本丰富性对深度学习模型的训练结果具有重要影响。现有的基于深度学习的光场显微三维重建方法数据集主要通过拍摄的方式获取,需要采用共聚焦扫描显微镜或选择平面照明显微镜等高分辨率成像设备,数据获取成本高,效率低,只适用于静态测量,且数据样本多样性有限,限制了深度学习技术在光场显微三维流场测量中的应用。
本文提出一种基于卷积神经网络深度学习模型的光场显微三维粒子分布重建方法,采用数值模拟方法构建“粒子空间分布-光场图像”数据集,进而搭建光场显微三维粒子分布卷积神经网络重建模型,并使用该模型对所建立的数据集进行学习和训练以获得粒子分布预测模型,并对预测模型的性能进行分析和评价。最后,通过微尺度层流流动速度场测量对所提方法的可行性进行实验研究。
2 基于卷积神经网络的光场显微粒子三维空间分布重建方法
2.1数据集建立
光场显微成像过程如图1所示。点光源发出的光线,经显微镜后会聚在微透镜阵列上,每个微透镜把接收光线按方向折射到其覆盖的传感器的不同像素上,形成离散的弥散斑。利用光线落在传感器上像素的坐标和对应微透镜的坐标,可以记录这条光线的方向和位置信息,获得的光场显微图像中的每个像素都对应记录着某个特定方向的光线。
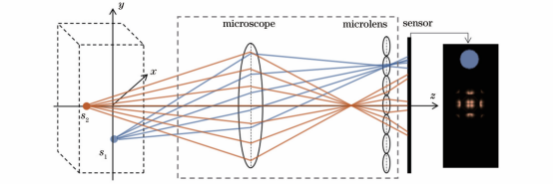
图1光场显微成像过程
由于光场显微成像系统中的衍射现象明显,需基于衍射理论分析显微镜筒镜像面经微透镜阵列二次成像在CCD传感器上的过程,建立光场显微成像模型。示踪粒子发出的光经光场显微成像系统的成像过程可用卷积[12]表示:
g(x,y,z)=h(x,y,z)*o(x,y,z)+n(x,y,z),(1)式中:o(x,y,z)为示踪粒子发出的光场;g(x,y,z)为像面的光强分布;h(x,y,z)为光场显微成像系统的点扩散函数(PSF);∗表示卷积运算;n(x,y,z)为系统噪声。可以看出,光场显微成像系统的成像模型主要由光场显微成像系统的点扩散函数决定。因此,通过确定点扩散函数,与示踪粒子光强分布进行卷积运算,即可确定CCD传感器面光强分布,从而获得光场图像。
基于上述光场显微成像模型可构建包含粒子光场图像和对应粒子空间分布的数据样本,具体如图2所示。首先,根据微通道参数定义测量体尺寸,并在测量体内随机选取粒子中心点位置;随后,将测量体内粒子三维光强分布与不同深度层点扩散函数进行卷积运算,获得粒子光场图像;最后,从光场图像中提取多个子孔径图像,从而构建“粒子光强分布-子孔径图像”数据集。数据集构建过程中,测量体尺寸为600×400×101体素,体素尺寸为0.55μm×0.55μm×1μm,粒子中心点位置随机分布。
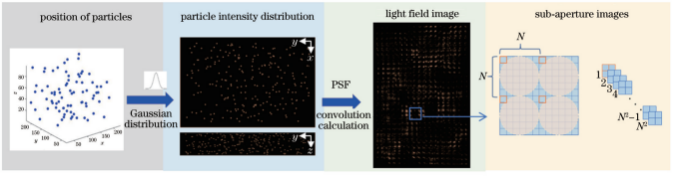
图2数据集建立流程
为了保证数值模型的可用性,粒子的发光特性需要与实际情况吻合。为此,通过实验拍摄的方式确定粒子的光强分布,光场显微镜的光学参数如表1所示,采集10倍物镜(数值孔径为0.3)下的示踪粒子图像(图3)计算粒子光强分布直径,具体数值为3.62μm,并将其作为数值模拟计算时的粒子直径,从而确定模拟过程中粒子光强分布的三维高斯分布:
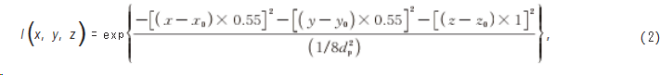
式中:I(x,y,z)为(x,y,z)处光强;dp为粒子光强分布直径;x0、y0、z0为粒子中心点三维坐标。
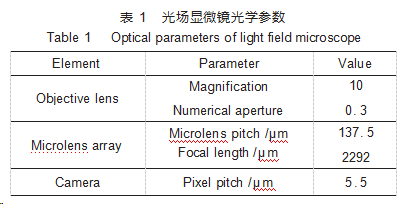

图3 10倍物镜下粒子发光直径
子孔径图像是光场图像中每个微透镜相同位置处像素组成的图像,模拟中光场图像每个微透镜覆盖像素数为25×25,因此共可提取625张子孔径图像。由于光场Mirco-PIV技术在实际应用中粒子随机分布,不同浓度下粒子的分布情况也不同,为保证数据集的丰富性和多样性,生成包含1000组样本的数据集,粒子浓度范围为0.4~1.2(以每个微透镜对应的粒子个数代表粒子浓度),数据集粒子浓度范围为0.4~1.2,总体平均浓度为0.8。生成粒子分布时,粒子中心位置随机生成,且粒子数量随粒子浓度上升而增加,不同粒子浓度的典型数据样本如图4所示。将数据集中所有样本混合并打乱顺序,划分为训练集和验证集两部分,划分比例为9∶1,训练集数据用于拟合网络,验证集数据用于检验模型状态和调整超参数。此外,为了评价模型的性能,构建一个包含100个数据样本的测试集,粒子浓度范围为0.3~1.2。

图4不同粒子浓度数据集样本。(a)(b)0.4;(c)(d)0.8;(e)(f)1.2
2.2卷积神经网络深度学习模型
卷积神经网络[26]能够通过卷积特征提取得到图像中的关键信息,相比于其他深度神经网络,更加适合用于图像数据处理[27],其中,U-Net模型结构简单,且能够实现像素级别的语义分割,性能优越。以U-Net模型为基础,基于光场显微粒子三维分布重建的实际需求开发的卷积神经网络模型如图5所示,网络输入为子孔径图像,经过上采样、编码和解码处理后输出粒子三维空间分布。
由于微透镜阵列的加入,光场显微成像过程比传统显微成像更为复杂,生成的光场图像也包含更丰富的光场信息。在数据集建立过程中,考虑到二维光场图像包含三维空间分布信息这一特征,进行了子孔径图像提取,所提取出的不同子孔径图像代表不同的角度信息,因此将子孔径图像作为多通道输入,再通过多层网络进行光场图像特征提取,从而实现映射关系的拟合。卷积核数量参考U-Net模型参数变化规律,基于输入通道数以及数据集图像尺寸确定。由于粒子三维空间分布不连续,且粒子尺寸相对于控制体来说较小,因此将学习率设置为10-5。
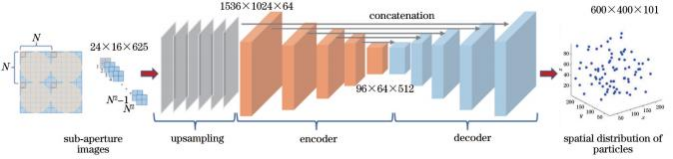
图5 用于光场显微粒子三维分布重建的卷积神经网络结构
在输入层,子孔径图像尺寸为24×16×625,上采样层对图片进行亚像素填充,以实现数据维度的扩充,经过多组上采样后,图像尺寸扩充为1536×1024×64。编码器部分(encoder)包含多个卷积层和池化层,卷积层对输入数据进行特征提取,池化层对数据进行降维,最终得到512个96×64的特征图。解码器部分(decoder)包含多个上采样层、卷积层和跳层连接层,上采样层用于恢复图像尺寸,跳层连接层用于融合特征,提高尺寸恢复过程的准确性。最终经过resize层,输出尺寸为600×400×101的三维粒子分布图像。
ReLU能够避免梯度消失问题,因此采用其作为卷积层激活函数。损失函数用于计算神经网络每次迭代的前向计算结果与真实值的差距,从而指导下一步的训练向正确的方向进行。训练过程中,损失函数越小,网络模型预测值就越接近真实值。采用真实图像和重建图像的均方误差(MSE)作为损失
函数:
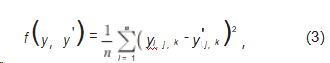
式中,yi,j,k和yi,'j,k分别为真实图像和重建图像中(i,j,k)位置处的灰度值。
网络训练采用Adam优化器,图6为网络模型损失函数随训练过程的变化情况,可以看出,随着迭代次数的增加,损失函数不断下降,在300个epoch后趋于稳定,因此选取训练300次的模型作为预测模型。
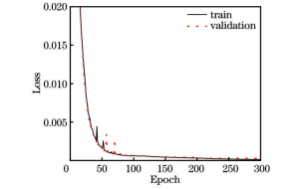
图6损失函数随训练过程的变化
3 重建算法检验
3.1图像重建评价指标
采用三维重建质量因子(Q)对训练得到的三维粒子分布重建模型的性能进行评价:
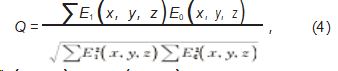
式中:E0(x,y,z)为位置(x,y,z)处示踪粒子精确的体素灰度值;E1(x,y,z)为位置(x,y,z)处重建示踪粒子的体素灰度值。三维重建质量因子Q的取值范围为0~1:Q=0表示重建的体素灰度分布与原始体素灰度分布完全不相交或重建的体素的灰度值为0;Q=1表示重建的体素灰度分布与原始体素灰度分布完全相同且对应体素的灰度值相等。Q值能够直接反映重建的示踪粒子分布和真实示踪粒子分布相似的程度,Q越大,图像重建质量越高。
半峰全宽(FWHM)可以用来评价单个粒子重建分辨率,如图7所示。FWHM表示单个粒子光强分布中峰值高度一半处的峰宽度,即通过峰高的中点作平行于峰底的直线,此直线与峰两侧相交两点之间的距离。半峰全宽越小,分辨率越高。
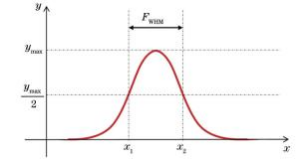
图7半峰全宽示意图
3.2三维空间分布重建结果
为评价预测网络模型性能,对测试集内的三维粒子空间分布进行重建。图8~10为LFD和预测模型两种方法对0.4、0.8、1.2等3种不同浓度粒子的重建结果。可以看出:与传统LFD算法相比,预测模型重建粒子在x方向与z方向强度分布均非常接近理论值。随着粒子浓度的增加,预测模型重建效果依然优于LFD算法。为定量评价粒子重建分辨率,表2给出了两种重建算法下不同浓度粒子的重建分辨率。在0.3~1.2的粒子浓度范围内,随机选取100组粒子光强分布数据进行半峰全宽计算,LFD算法重建粒子水平方向半峰全宽为(2.45±0.18)μm(均值±标准差),深度方向半峰全宽为(11.30±0.60)μm。预测模型重建粒子在水平方向半峰全宽为(2.20±0.11)μm,深度方向半峰全宽达(2.34±0.11)μm,粒子拉伸明显减小。总体而言,两种方法重建粒子水平方向分辨率相当,但在深度方向上,预测模型重建分辨率相较于LFD算法提升了79.3%,体现出显著的优越性。
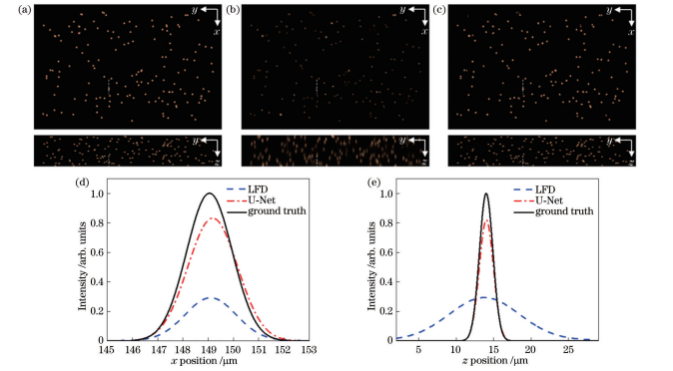
图8 0.4浓度粒子空间分布和单粒子(虚线所示)光强分布。(a)粒子理论分布;(b)LFD重建粒子分布;(c)预测模型重建粒子分布;(d)粒子沿x方向光强分布;(e)粒子沿z方向光强分布
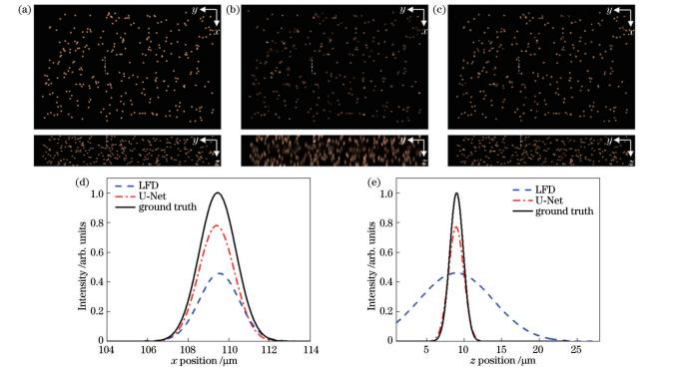
图9 0.8浓度粒子空间分布和单粒子(虚线所示)光强分布。(a)粒子理论分布;(b)LFD重建粒子分布;(c)预测模型重建粒子分布;(d)粒子沿x方向光强分布;(e)粒子沿z方向光强分布
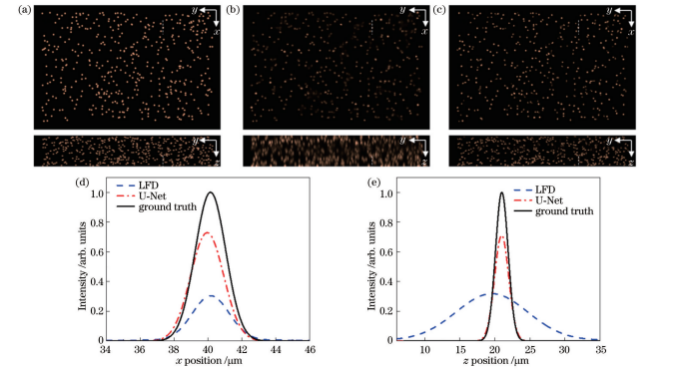
图10 1.2浓度粒子空间分布和单粒子(虚线所示)光强分布。(a)粒子理论分布;(b)LFD重建粒子分布;(c)预测模型重建粒子分布;(d)粒子沿x方向光强分布;(e)粒子沿z方向光强分布
图11为不同粒子浓度下预测模型和LFD两种方法重建质量因子对比,可以看出:粒子浓度在0.3~0.6范围内时,预测模型的重建质量因子可达0.8以上,而同样粒子浓度下,LFD的重建质量因子为0.5~0.6;随着粒子浓度增加到0.7~1.0,预测模型的重建质量因子下降至0.7~0.8之间,LFD的重建质量因子也略有降低;粒子浓度升高至1.1~1.2时,预测模型的重建质量因子下降至0.65~0.68,LFD的重建质量因子则下降至0.48~0.5之间。总体而言,当粒子浓度为0.3~1.2时,随着粒子浓度增加,两种方法重建质量因子均有所下降。然而,由于预测模型重建粒子轴向拉伸明显小于LFD算法,轴向分辨率较高,预测模型的重建质量因子始终高于传统反卷积重建算法。
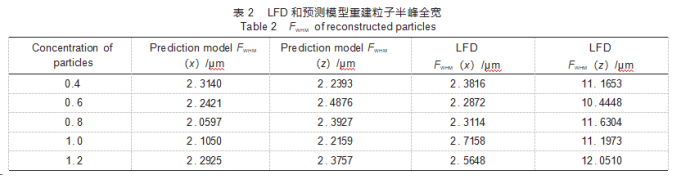
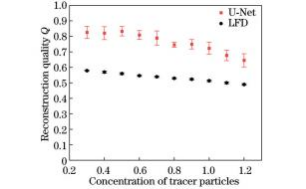
图11不同浓度粒子重建质量
图12为预测模型和LFD两种方法粒子提取率对比,可以看出:粒子浓度在0.4~0.8范围内时,LFD和预测模型的粒子提取率维持在90%以上;随着粒子浓度增加到1.0~1.2,两种方法提取率均处于80%~90%之间。总体而言,粒子浓度在0.4~1.2范围内时,两种方法的粒子提取率相近。
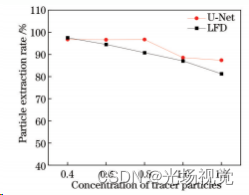
图12不同浓度粒子提取率
3.3重建时间
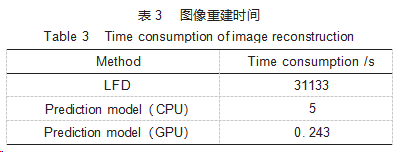
在模型学习和训练过程中,所使用计算机的CPU和GPU分别为inteli9-10940X和NVDIAGeForceRTX3090,深度学习模型是在Windows环境下基于TensorFlow框架实现。采用数值计算构建模拟数据集,数据集构建时间为23.1s/组,对1000组数据样本训练300个epoch花费的时间约为23h。获得的预测模型与常规的LFD算法的重建效率比较如表3所示。可以看出:采用LFD算法进行重建时,每幅图像的重建时间为31133s,而基于CPU计算的预测模型重建时间为5s,基于GPU计算的预测模型重建时间仅为0.243s,即预测模型相比LFD算法重建效率大大提升。
4 抗噪性能
在实际测量过程中,所采集到的光场图像存在一定的噪声,因此需要对所提出的三维空间分布重建方法进行抗噪性能评估。图13为预测模型和LFD对不同信噪比(RSN)光场图像重建的粒子分布结果,对应的重建质量因子Q如图14所示。可以看出:信噪比低于5dB时,LFD算法重建粒子光强较弱;信噪比达到5dB及以上时,重建粒子光强增加,可轻易分辨粒子分布,预测模型重建粒子分布情况与理论分布差别不明显,表明噪声对预测模型的影响不大。随着信噪比上升,两种方法的重建质量因子均有所上升,预测模型的重建质量因子始终高于传统反卷积重建算法。图15为预测模型对RSN=10的不同粒子浓度光场图像重建质量。可以看出:噪声的加入将导致重建质量因子的轻微下降,但重建质量因子依然高于无噪声情况下LFD重建结果。整体而言,预测模型的抗噪能力较好。

图13预测模型和LFD对不同信噪比光场图像重建的粒子分布
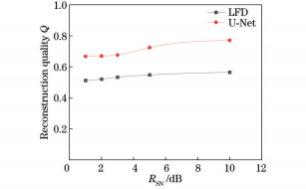
图14预测模型和LFD对不同信噪比光场图像重建质量
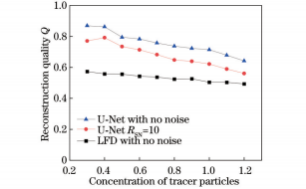
图15预测模型对RSN=10的不同粒子数光场图像重建质量
4 光场显微层流流场测量实验验证
4.1实验系统
为了测试光场显微三维粒子空间分布预测模型的泛化能力和实用性,进行了微尺度层流流场测量实验研究。微尺度流动测量系统如图16所示,主要包括激光器、显微镜、注射泵、微尺度通道、同步控制器、光场相机、计算机等设备。光场显微镜采用10倍物镜,数值孔径为0.3。采用微尺度通道进行水平层流流动测量实验,微尺度通道宽度为300μm,深度为100μm。示踪粒子为直径2μm的荧光聚苯乙烯微球,实验过程中,通道入口处示踪粒子溶液流速为7μL/min。测量系统以2000μs的两帧间隔采集粒子光场图像,这里随机选取一组图像进行重建。
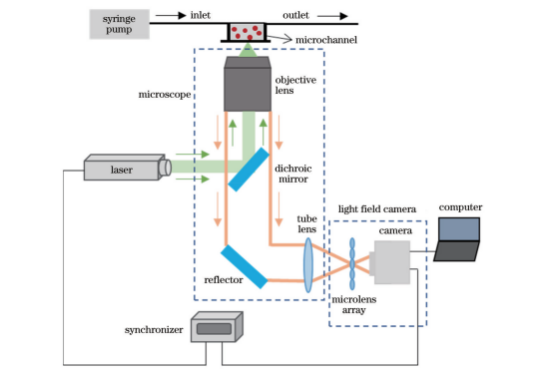
图16微尺度流动测量实验装置
4.2实验结果与讨论
典型的粒子光场图像以及其粒子分布重建结果如图17所示。可以看出:相较于预测模型,LFD重建粒子分布图像相对较暗,光强较低,这与模拟重建中LFD重建的光强较低的情况相吻合,但两种方法重建的粒子位置分布基本一致。粒子实际发光直径为3.62μm,由于粒子各向同性,粒子光强分布在x方向和z方向半峰全宽均为2.13μm,预测模型重建粒子在x方向和z方向光强分布半峰全宽分别为2.14μm和2.38μm,反卷积方法重建粒子在x方向和z方向光强分布半峰全宽分别为2.82μm和13.20μm。可以看出,预测模型重建粒子在深度方向拉伸大大减小,与数值模拟结果相符。
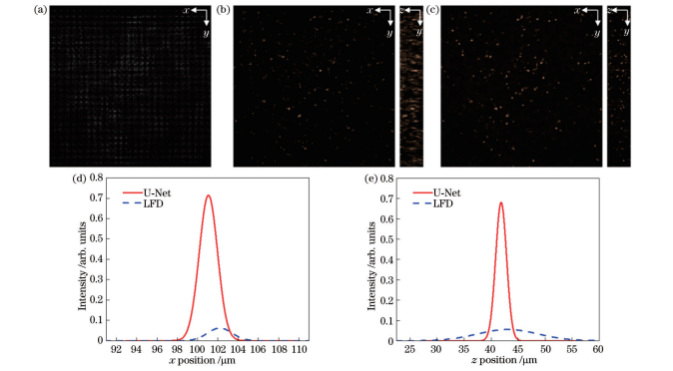
图17实验光场图像及其重建粒子分布。(a)实验拍摄光场图像;(b)LFD重建粒子分布;(c)预测模型重建粒子分布;(d)粒子沿x方向光强分布对比;(e)粒子沿z方向光强分布对比
为了进一步验证所提出的光场显微粒子空间分布卷积神经网络重建模型的实用性,采用三维互相关算法对其重建的粒子场进行分析,计算微通道层流流动的三维速度场。速度场计算过程中,互相关窗口尺寸为70.4μm×70.4μm×20μm,重叠率为0.5。图18为预测模型测得的三维速度场,微流体沿x方向流动,近壁面处流速较小,管道中心位置流速较大,整体流速处于10-3m/s数量级。为了评估测量精度,将预测模型获得的测量速度场与LFD算法测量速度场和理论值进行比较。理论速度由数值模拟计算获得:首先根据微通道尺寸建立水平微尺度通道模型并划分网格,再基于计算流体力学平台AnsysFluent的层流模型进行计算[12,28]。图19为z=50μm处预测模型和LFD算法实测速度与理论速度的对比结果,LFD算法和预测模型获得的测量结果与理论值基本一致,流速保持抛物线分布,这与理论流动相吻合。为定量评价所测速度场,定义相对偏差ve:
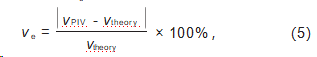
式中:vPIV和vtheory分别为实验测得的速度值和理论值。LFD算法和预测模型在z=50μm处的平均相对偏差分别为15.38%和15.17%,其中,两种方法测量速度场近壁面处速度值相对偏差均较大,这是因为实验流动过程中,近壁面处速度梯度大,粒子浓度低,互相关计算时近壁面处速度值难以捕捉。总体而言,预测模型和LFD算法的速度场测量精度相当,验证了所构建预测模型在三维速度场测量的实用性。
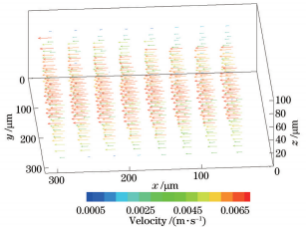
图18预测模型获得三维速度场
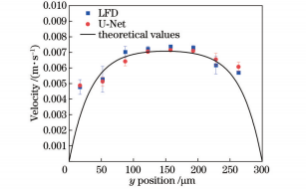
图19z=50μm处实测速度与理论速度对比
5 结论
提出一种基于卷积神经网络深度学习模型的光场显微粒子三维空间分布重建方法,通过数值模拟高效构建的“粒子空间分布-光场图像”数据集对建立的卷积神经网络模型进行训练与性能测试,并实现了水平微通道层流流动中粒子分布的实验重建。结果表明:相比常规的反卷积方法,所提方法的粒子重建轴向分辨率提高了79.3%,单张图像重建时间为常规反卷积算法的0.0078‰,证明了所提方法的优越性。为了验证所提方法重建的粒子分布对三维速度场测量的可用性,利用互相关算法计算水平微通道层流的三维速度场,获得的速度场与CFD数值模拟、反卷积算法结果均一致,进一步验证了所提方法的可行性和有效性。
内容来源:光学学报 第43卷 第21期
作者:沈诗宇,李健,顾梦涛,张彪,许传龙
东南大学大型发电装备安全运行与智能测控国家工程研究中心
声明:转载此文目的在于传递更多信息,仅供读者学习、交流之目的。文章版权归原作者所有,如有侵权,请联系删除。