图论基础|深度优先dfs、广度优先bfs

dfs 与 bfs 区别

提到深度优先搜索（dfs），就不得不说和广度优先搜索（bfs）有什么区别

先来了解dfs的过程，很多录友可能对dfs（深度优先搜索），bfs（广度优先搜索）分不清。

先给大家说一下两者大概的区别：

dfs是可一个方向去搜，不到黄河不回头，直到遇到绝境了，搜不下去了，再换方向（换方向的过程就涉及到了回溯）。
bfs是先把本节点所连接的所有节点遍历一遍，走到下一个节点的时候，再把连接节点的所有节点遍历一遍，搜索方向更像是广度，四面八方的搜索过程。

深度优先dfs

深度优先关键就两点：

搜索方向，是认准一个方向搜，直到碰壁之后再换方向
换方向是撤销原路径，改为节点链接的下一个路径，回溯的过程。

其实深搜和回溯是非常类似的，深搜三部曲如下：

1.确认递归函数，参数

void dfs(参数)

通常我们递归的时候，我们递归搜索需要了解哪些参数，其实也可以在写递归函数的时候，发现需要什么参数，再去补充就可以。

一般情况，深搜需要二维数组数组结构保存所有路径，需要一维数组保存单一路径，这种保存结果的数组，我们可以定义一个全局变量，避免让我们的函数参数过多。

vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs (图，目前搜索的节点)

2.确认终止条件

终止条件很重要，很多同学写dfs的时候，之所以容易死循环，栈溢出等等这些问题，都是因为终止条件没有想清楚。

if (终止条件) {
    存放结果;
    return;
}

终止添加不仅是结束本层递归，同时也是我们收获结果的时候。

另外，其实很多dfs写法，没有写终止条件，其实终止条件写在了，下面dfs递归的逻辑里了，也就是不符合条件，直接不会向下递归。

3.处理目前搜索节点出发的路径

一般这里就是一个for循环的操作，去遍历目前搜索节点所能到的所有节点。

for (选择：本节点所连接的其他节点) {
    处理节点;
    dfs(图，选择的节点); // 递归
    回溯，撤销处理结果
}

797.所有可能的路径

力扣题目链接(opens new window)

给你一个有 n 个节点的有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

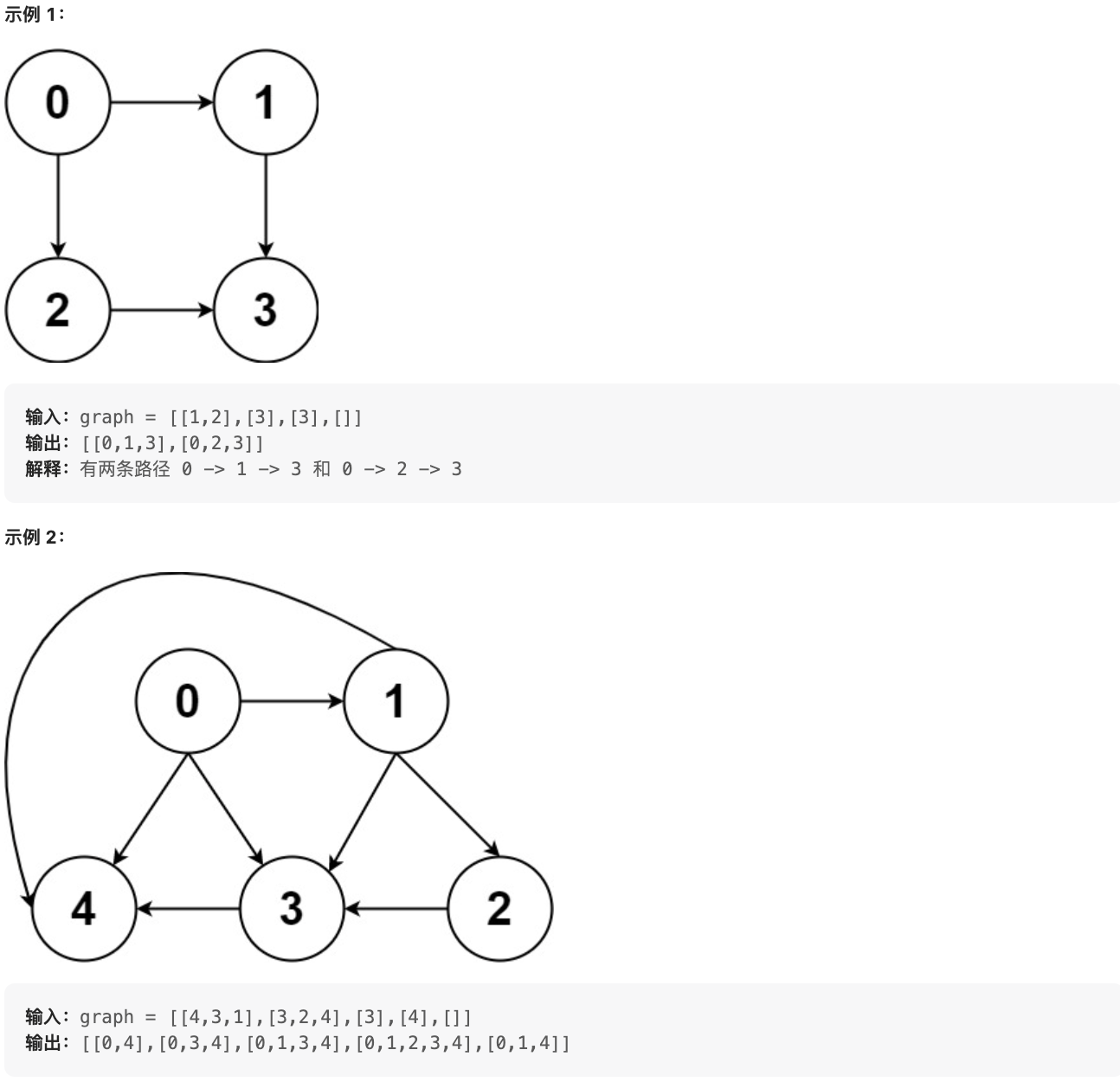
提示：

n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i（即不存在自环）
graph[i] 中的所有元素互不相同
保证输入为有向无环图（DAG）

思路：深度优先基础题目

class Solution {
public:
    vector<vector<int>>result;
    vector<int>path;
    void dfs(vector<vector<int>>& graph, int x){
        if(x==graph.size()-1){//搜索到终点，停止搜索并把可行路径加入结果数组
            result.push_back(path);
            return;
        }

        for(int i=0; i<graph[x].size(); i++){//遍历节点所能访问的所有其他节点
            path.push_back(graph[x][i]);
            dfs(graph, graph[x][i]);//递归遍历
            path.pop_back();//回溯
        }
    }
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        result.clear();
        path.clear();
        path.push_back(0);//从0节点出发
        dfs(graph,0);//从节点0开始搜索
        return result;
    }
};

广度优先搜索理论基础

广度优先类似于二叉树的层序遍历

广搜的搜索方式就适合于解决两个点之间的最短路径问题。因为广搜是从起点出发，以起始点为中心一圈一圈进行搜索，一旦遇到终点，记录之前走过的节点就是一条最短路。

上面我们提过，BFS是一圈一圈的搜索过程，但具体是怎么一圈一圈来搜呢。

我们用一个方格地图，假如每次搜索的方向为上下左右（不包含斜上方），那么给出一个start起始位置，那么BFS就是从四个方向走出第一步。

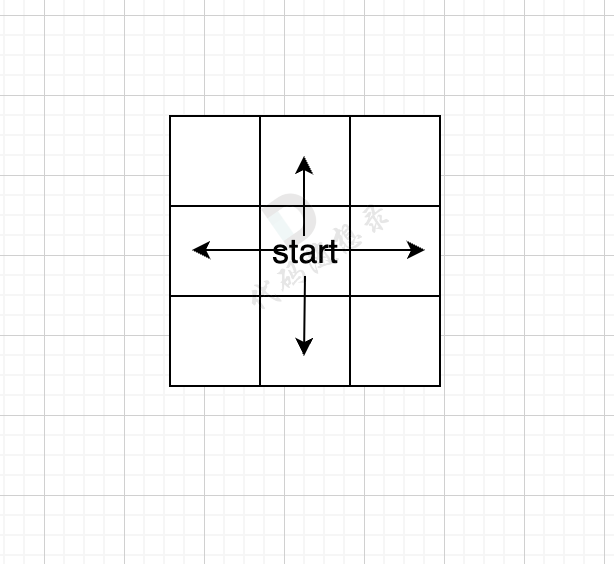
如果加上一个end终止位置，那么使用BFS的搜索过程如图所示：

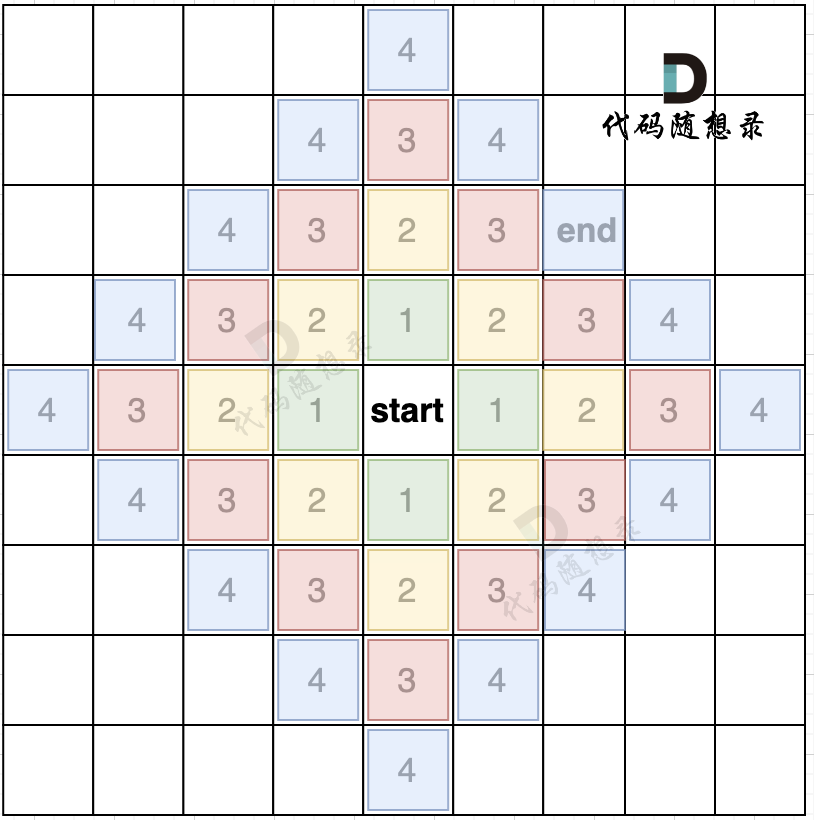
我们从图中可以看出，从start起点开始，是一圈一圈，向外搜索，方格编号1为第一步遍历的节点，方格编号2为第二步遍历的节点，第四步的时候我们找到终止点end。

正是因为BFS一圈一圈的遍历方式，所以一旦遇到终止点，那么一定是一条最短路径。

大家应该好奇，这一圈一圈的搜索过程是怎么做到的，是放在什么容器里，才能这样去遍历。

很多网上的资料都是直接说用队列来实现。

其实，我们仅仅需要一个容器，能保存我们要遍历过的元素就可以，那么用队列，还是用栈，甚至用数组，都是可以的。

用队列的话，就是保证每一圈都是一个方向去转，例如统一顺时针或者逆时针。

因为队列是先进先出，加入元素和弹出元素的顺序是没有改变的。

如果用栈的话，就是第一圈顺时针遍历，第二圈逆时针遍历，第三圈有顺时针遍历。

因为栈是先进后出，加入元素和弹出元素的顺序改变了。

那么广搜需要注意转圈搜索的顺序吗？不需要！

所以用队列，还是用栈都是可以的，但大家都习惯用队列了，所以下面的讲解用我也用队列来讲，只不过要给大家说清楚，并不是非要用队列，用栈也可以。

广搜代码模板，该模板针对的就是，上面的四方格的地图：（详细注释）

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图，也就是一个二维数组
// visited标记访问过的节点，不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
    queue<pair<int, int>> que; // 定义队列
    que.push({x, y}); // 起始节点加入队列
    visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点
    while(!que.empty()) { // 开始遍历队列里的元素
        pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
        int curx = cur.first;
        int cury = cur.second; // 当前节点坐标
        for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过
            if (!visited[nextx][nexty]) { // 如果节点没被访问过
                que.push({nextx, nexty});  // 队列添加该节点为下一轮要遍历的节点
                visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问
            }
        }
    }

}

200. 岛屿数量

题目链接(opens new window)

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 '0' 或 '1‘

广度优先版本：

class Solution {
public:
    int dir[4][2]={0,1,1,0,-1,0,0,-1};//定义四个方向
    void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y){
        queue<pair<int,int>> que;
        que.push({x,y});
        while(!que.empty()){
            pair<int, int> cur=que.front(); que.pop();//出队，访问
            int curx=cur.first;
            int cury= cur.second;
            visited[curx][cury]=true;//标记该节点访问过
            for(int i=0;i<4;i++){
                int nextx=curx+dir[i][0];
                int nexty=cury+dir[i][1];
                //判断是否超出边界
                if(nextx<0||nextx>=grid.size()||nexty<0||nexty>=grid[0].size())continue;
                if(!visited[nextx][nexty]&&grid[nextx][nexty]=='1'){
                    que.push({nextx,nexty});
                    visited[nextx][nexty]=true;
                }
            }

        }
    }
    int numIslands(vector<vector<char>>& grid) {
        int result=0;
        int n=grid.size();
        int m=grid[0].size();
        vector<vector<bool>>visited(n, vector(m,false));
        

        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(!visited[i][j]&&grid[i][j]=='1'){
                    result++;
                    bfs(grid,visited,i,j );
                }
            }
        }
        return result;
    }
};

深度优先版本：

class Solution {
public:
    int dir[4][2]={0,1,1,0,-1,0,0,-1};//定义四个方向
    void dfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y){
        for(int i=0;i<4;i++){
            int nextx=x+dir[i][0];
            int nexty=y+dir[i][1];
            if(nextx<0||nextx>=grid.size()||nexty<0||nexty>=grid[0].size())continue;
            if(!visited[nextx][nexty]&&grid[nextx][nexty]=='1'){
                visited[nextx][nexty]=true;
                dfs(grid,visited,nextx,nexty);
            }
        }
    }
    int numIslands(vector<vector<char>>& grid) {
        int result=0;
        int n=grid.size();
        int m=grid[0].size();
        vector<vector<bool>>visited(n, vector(m,false));
        

        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(!visited[i][j]&&grid[i][j]=='1'){
                    result++;
                    dfs(grid,visited,i,j );
                }
            }
        }
        return result;
    }
};

参考：代码随想录