本专栏内容整理了GAMES101的计算机图形学课程的主要内容，作为我学习计算机图形学的一份复习备份或叫做笔记。内容中如有错误，或有其他建议，欢迎大家指出。

附上GAMES101计算机图形学课程：GAMES101: 现代计算机图形学入门正在上传…重新上传取消https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html正在上传…重新上传取消https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html​编辑https://sites.cs.ucsb.edu/~lingqi/teaching/games101.htmlhttps://sites.cs.ucsb.edu/~lingqi/teaching/games101.html

GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibiliGAMES101-现代计算机图形学入门-闫令琪共计23条视频，包括：Lecture 01 Overview of Computer Graphics、Lecture 02 Review of Linear Algebra、Lecture 03 Transformation等，UP主更多精彩视频，请关注UP账号。正在上传…重新上传取消https://www.bilibili.com/video/BV1X7411F744正在上传…重新上传取消https://www.bilibili.com/video/BV1X7411F744​编辑https://www.bilibili.com/video/BV1X7411F744https://www.bilibili.com/video/BV1X7411F744

三角形重心坐标插值法是什么

先来个gpt的回答

三角形重心坐标插值法是一种在计算机图形学中常用的技术，它允许我们在三角形内部平滑地插值顶点的任何属性，如位置、纹理坐标、颜色、法线、深度和材质属性。这种方法基于重心坐标，这是由三角形的三个顶点定义的坐标系统。

在三角形的重心坐标系统中，三角形上的任意一点 ( p ) 可以表示为三个顶点 ( A ), ( B ), 和 ( C ) 的线性组合：

p=w1​⋅A+w2​⋅B+w3​⋅C

其中，( w1 ), ( w2 ), 和 ( w3 ) 是权重系数，它们满足以下条件：

w1​+w2​+w3​=1

并且每个系数都是非负的。当这些条件满足时，点 ( p ) 就位于三角形内部。这些权重系数代表了点 ( p ) 相对于三角形顶点的位置。

例如，如果我们有三角形顶点的颜色 ( C1 ), ( C2 ), 和 ( C3 )，那么内部点 ( p ) 的颜色 ( Cp ) 可以通过以下方式插值得到：

Cp​=w1​⋅C1​+w2​⋅C2​+w3​⋅C3​

-----------------------------------------------------------------------------------------------------------------------------

为什么要做插值

在计算机图形学中，我们经常需要对三角形内部的内容进行填充。比如着色阶段，我们需要得到三角形内部的各个像素位置的法向量，纹理映射时需要得到三角形内部像素对应在纹理贴图上的哪一个uv区域，还有得到顶点颜色，我们要在三角形内部平滑地过渡这三个颜色。这都需要用插值的方法。

我们为什么要插值？
•指定顶点处的值
•获得三角形间平滑变化的值
我们想要插值什么？
•纹理坐标、颜色、法线向量…

怎么做插值

所谓插值，可以理解为我们小学常做的数学题，找规律。比如：在0~10中间填入4个数字。那就是2,4,6,8；

这里我们需要做的比小学数学题难，我们需要对二维的三角形内部空间做插值。我们就需要引入一个辅助点——叫三角形重心坐标。

三角形重心坐标

重心是物理学中的一个概念，指的是一个物体上所有质量的平均位置，也就是物体受到重力作用时所有质量元素所受重力的合力作用点。在均匀重力场中，无论物体处于何种方位，其重力总是通过这一点。对于形状规则且质量分布均匀的物体，重心通常位于几何中心。例如，一个均匀的直棒的重心就在其长度的中点，一个圆的重心就在圆心。

在三角形中，有一个点，将这个点与三角形的三个顶点连接，能将三角形分为三个小的三角形，且这三个三角形的面积相等。这个点就是三角形的重心。

在三角形中，重心是三条中线的交点，也就是连接三角形每个顶点和对边中点的线段相交的点。

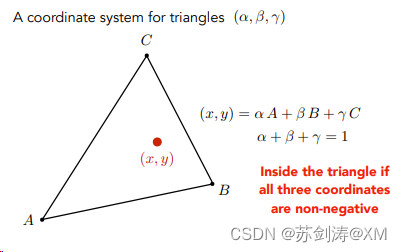
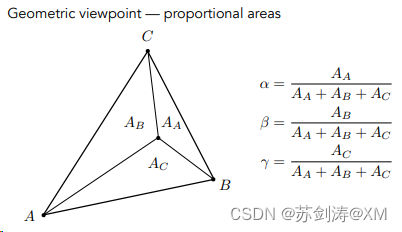
在三角形中，三角形内部的任何一个点都可以表示为由三角形的三个顶点A,B,C的的线性组合（左图），该线性组合需要满足系数α，β，γ加起来一定等于1，α，β，γ都是非负数。

比如对于A点的坐标，用这个线性组合表示就如右图

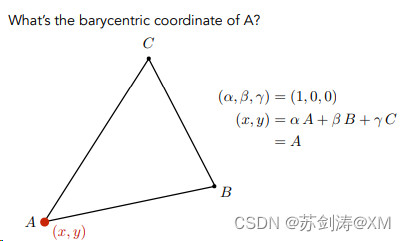
对于三角形内部的任何一点，我们都可以连接这个点到各个订单得到三个三角形。三角形的每个顶点对面都有一个小三角形。比如A点对面是三角形AA，B点对面是AB， C点对面是AC。

α系数的值就是A点对面的三角形AA的面积除以总的三角形的面积；

β和γ同理。

于是因为三角形重心可以将三角形分为面积相等的三个三角形。所以我们就可以得到三角形的重心点的α，β，γ值都是1/3。那么比如我们要在重心位置插值出该点的颜色，就是1/3A点颜色+1/3B点颜色+1/3C点的颜色。

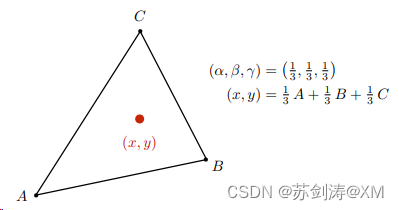
那么我们要得到三角形内部任意一个点的属性插值，就只需要知道α，β，γ的值，通过配比A，B，C三个顶点的属性值就行。

α，β，γ求值的公式见下图。

 需要注意的是，在透视投影变换后，三角形的形状会发生变化，同样，重心位置也会发生变化。投影后相同的三个系数值，无法对应到原三角形的同系数值的位置上。或者说，同一个点在投影后，位置会发生改变，α，β，γ会发生改变。
在三维空间中的属性要在三维空间中做好插值再透视投影到二维空间中去。但是光栅化过程中，三角形内部像素的一些属性插值必须发生在透视投影变换后。那么：

我们要做透视校正插值 (Perspective-Correct Interpolation)。

对于逆投用变换再变换回2d的方法去做三维空间的插值会消耗比较多的性能。所以我们使用另一个透视校正插值的方法。透视校正插值会使用投影后的插值系数的倒数之间的线性关系来计算属性值。

这里我直接给出计算深度属性Z的一个透视校正插值公式（计算其他属性也是一样的）：

其中Z，Z_A，Z_B, Z_C 都是3D空间中的属性，α’，β’，γ’是2D屏幕上的配比参数。

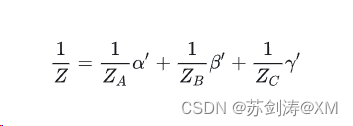
 对比普通的三角形重心线性插值，对于在2D空间求3D空间属性的透视校正插值刚好每一个顶点参数都是普通的三角形重心线性插值顶点属性的倒数，结果属性也是倒数。So Amazing！！！！。