1、多项式回归回顾

本文接上篇：Scikit-Learn逻辑回归(一)

上篇中，我们详细介绍了逻辑回归的概念、原理和推导，以及Scikit-Learn线性回归模型在鸢尾花数据集中的应用。本文主要介绍如何在逻辑回归中使用多项式特征、正则化

1.1、逻辑回归为什么要使用多项式

首先来看一个例子。准备二分类样本数据并绘制：

import numpy as np
import matplotlib.pyplot as plt

# 随机数种子，只需设置一次，设置后只要种子不变，每次生成相同的随机数
np.random.seed(666)
# 构建均值为0，标准差为1（标准正态分布）的矩阵，200个样本
X = np.random.normal(0, 1, size=(200, 2))
# 构建一个生成y的函数，将y以>1.5还是<1.5进行分类
y = np.array(X[:, 0] ** 2 + X[:, 1] ** 2 < 1.5, dtype='int')
# 绘制样本数据
plt.xlim(-4, 4)
plt.ylim(-4, 4)
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()

样本数据分布如图所示：

使用逻辑回归（二分类）训练模型：

from sklearn.linear_model import LogisticRegression

# 训练逻辑回归模型
lr = LogisticRegression()
lr.fit(X, y)

# 准确度评分
print(lr.score(X, y))   # 0.605

绘制该样本数据在逻辑回归模型上的决策边界（函数详解见上篇）：

# 绘制决策边界
decision_boundary(lr, axis=[-4, 4, -4, 4])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()

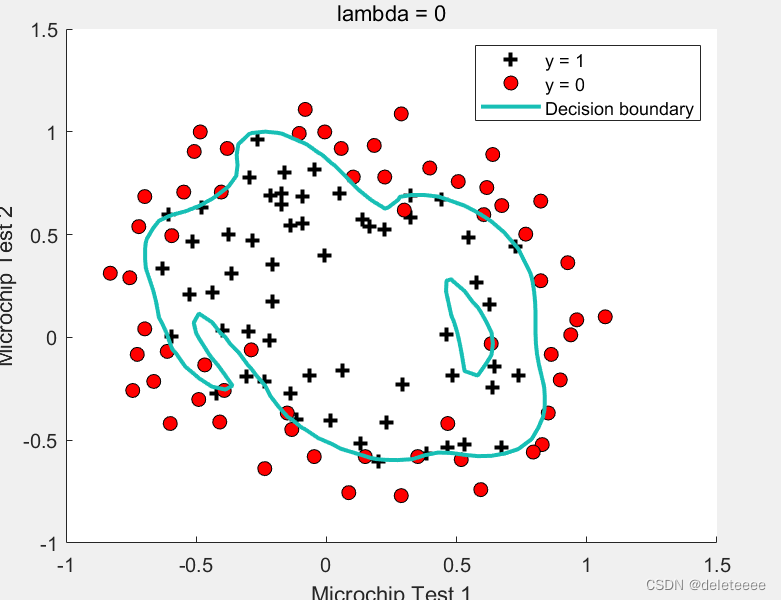
决策边界如图所示：

从图中可以看到，我们线性决策边界明显无法将样本分成两类，训练的模型准确度评分很低

从样本数据图可以看出，二分类的决策边界应该是一个圆或椭圆。圆的标准方程为
$$(x-a{)}^2+(y-b{)}^2=r^2$$

将圆沿特定方向压缩或伸长即可得到椭圆（标准方程）：
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

下面以圆为例说明。(a,b)为圆心，r为半径。设圆心在(0,0)，则变换圆的标准方程可得
$$x^2+y^2-r^2=0$$

而逻辑回归（二分类）的线性决策边界（详见上篇）为
$${\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2=0$$

通过对比，我们发现只需要给线性决策边界的特征增加幂次即可，即使用多项式特征

1.2、多项式回归及原理

更多关于多项式回归及其原理的详解见文章：传送门

2、逻辑回归与多项式

如果逻辑回归处理的是不规则决策边界的分类问题，那么我们就应该多考虑运用多项式回归

为方便起见，我们使用Scikit-Learn提供的管道工具（详见：传送门）。以下是一个为逻辑回归添加多项式特征并使用管道的示例：

构建多项式逻辑回归模型管道：

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler

# 构建多项式逻辑回归模型管道
def PolyLogisticRegression(degree):
    return Pipeline([
        ('poly', PolynomialFeatures(degree=degree)),
        ('std_sca', StandardScaler()),
        ('lr', LogisticRegression())
    ])

训练多项式逻辑回归模型：

# 实例化多项式逻辑回归模型
plr = PolyLogisticRegression(degree=2)
# 训练
plr.fit(X, y)
# 准确度评分
print(plr.score(X, y))   # 0.96

可以看到，在逻辑回归中应用了多项式特征后，我们训练出的新模型对样本数据的预测评分达到了0.96。下面再来绘制一下其决策边界：

# 绘制决策边界
decision_boundary(plr, axis=[-4, 4, -4, 4])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()

决策边界如图所示：

可见，圆形的决策边界对样本数据的类型区分更加准确

未完待续…

参考文章：https://www.cnblogs.com/jokingremarks/p/14321097.html