一、目的和要求

1.编程实现Logistic Regression并应用于数据集；

2.绘制二元分类函数、sigmoid函数和代价函数；

3.正则化logistic回归代价。

二、算法介绍

步骤：

选择一个合适的分类函数来实现分类（Sigmoid函数）

通过损失函数（Cost函数）来表示预测值（h(x)）与实际值(y)的偏差(h−y),要使得回归最佳拟合，那么偏差要尽可能小（偏差求和或取均值）。

记J(θ)J表示回归系数为θ时的偏差，那么求最佳回归参数θ就转换成了求J(θ)的最小值。

Sigmoid函数：

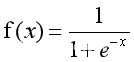
代价函数：

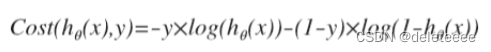
正则化logistic 回归

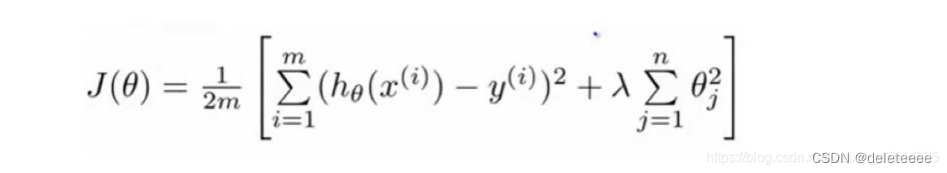
fminunc函数：Matlab内置最小值优化函数，可以代替梯度下降法求解最优θ值。

三、过程记录

（1）对数几率回归

1.数据可视化

分析数据集可知数据集的三列数据分别为第一次成绩，第二次成绩以及是否录取（1表示录取，0表示未录取）。读入数据集后可以将两次成绩分别作为横纵坐标，在通过判断是否录取绘制不同形状的散点。

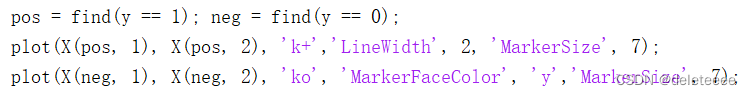
结果如下：

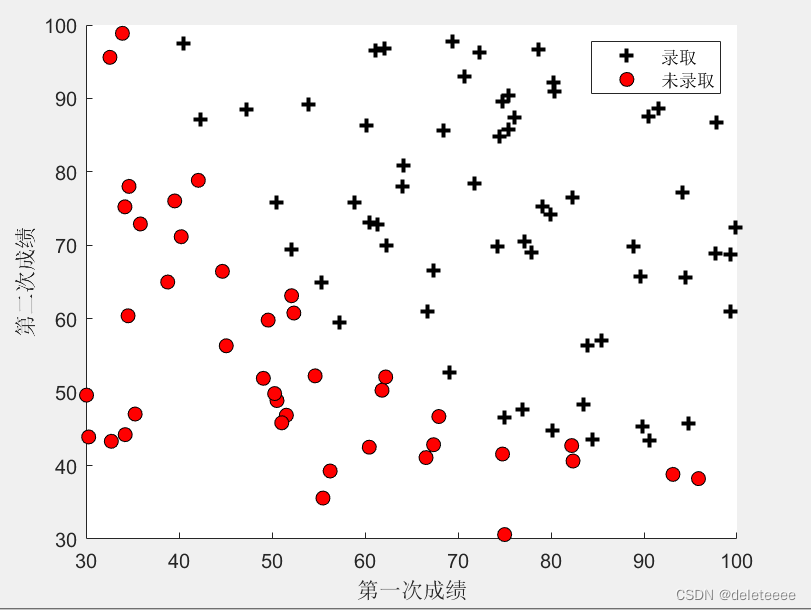
图1 数据集分布散点图

2.获得成本和梯度

计算成本函数和梯度时需要用到sigmoid函数，为了方便，通过公式提前编写sigmoid函数：g = 1./ ( 1 + exp(-z) ) ;参数z可以是矩阵

接下来需要计算成本和梯度，利用sigmoid函数通过如下公式实现：

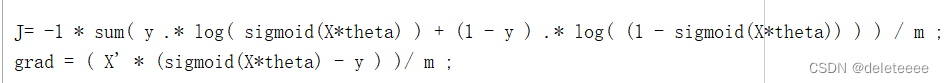
其中theta初始为0矩阵

结果如下：

图2 代价和梯度初始值

3.寻找最佳theta参数

通过内置函数fminunc实现，首先设置好相应参数，然后再给函数传入初始theta参数以及成本和梯度函数，如下：

经过迭代后寻找的最后结果如图所示：

图3 优化后的代价以及theta值

通过theta值可以绘制出决策边界，我的做法如下：

绘制的结果如下：

图4 决策边界

此时利用数据集绘制sigmoid函数图像结果如下：

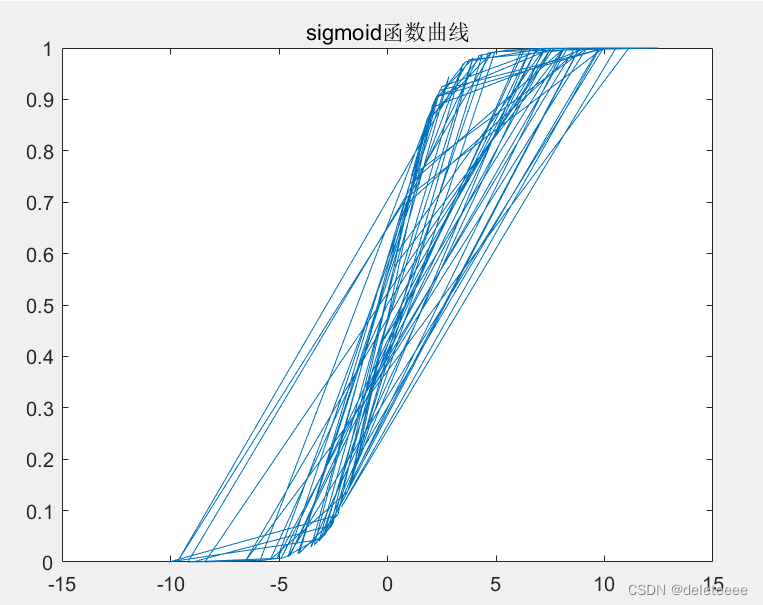
图5 sigmoid函数图像

由于数据集中数据分布不规则所以导致绘制的图像较为混乱，如果设定一个规则的数据集：z=[ones(m,1) [1:100]' [1:100]'];以此来绘制sigmoid图像结果如下：

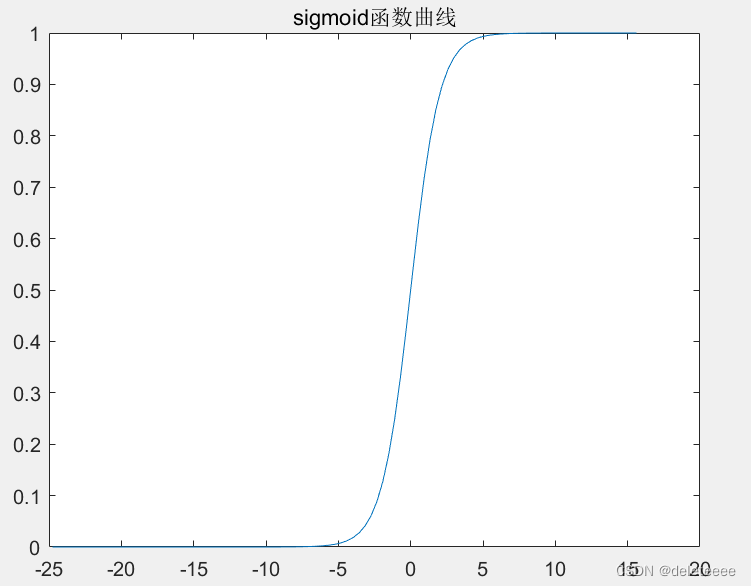
图6 修改后的sigmoid图像

此时可以清晰的看出sigmoid函数的变换趋势

4.预测并计算训练集精确度

预测两次成绩分别为45 85的学生被录取的概率，通过sigmoid函数可以求出。而预测是否录取则可以通过判断概率是否大于0.5，大于0.5的判断为录取否则为未录取。将训练集样本进行预测并通过比对可以得到精确度。结果如下：

图7 预测概率及精确度

（2）正则化logistic回归

1.数据可视化

绘制数据集2的散点图：

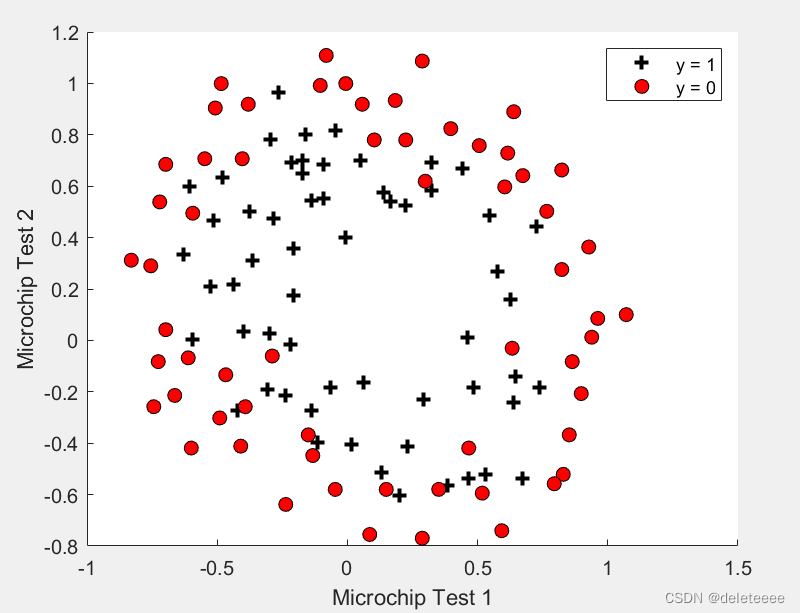
图8 数据分布散点图

从散点图中可以看出此时无法再像第一个实验那样通过直线来分割两类数据了

2.特征映射

为了更好的拟合数据，需要为每个数据点创建更多的特征，实现如下

经过转换后原来的两个特征向量变成了28维向量

3.计算代价函数和梯度

将theta初始为0矩阵，lambda设为1，正则化成本函数和梯度公式如下，其中theta索引为1的参数即θ0不用正则化。

此时结果为

图9 初始代价和梯度值

4.寻找最佳theta值

依然通过fminunc函数进行运算，结果如下

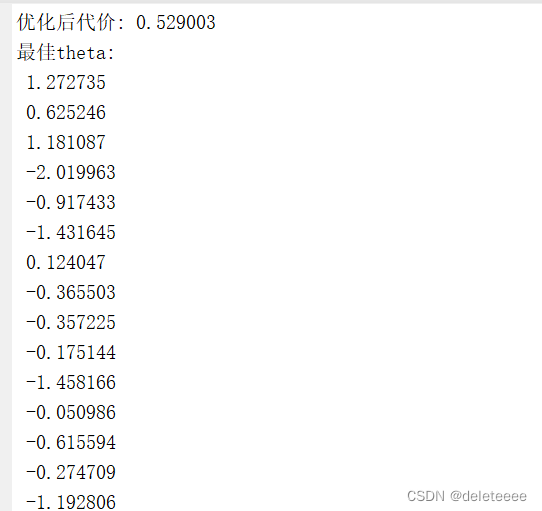
图10 优化后的代价及theta值

5.绘制决策曲线

由于本例无法通过直线来进行划分，可以采用matlab内置contour函数以等高线的方式绘制出边界，代码如下：

最终边界线：

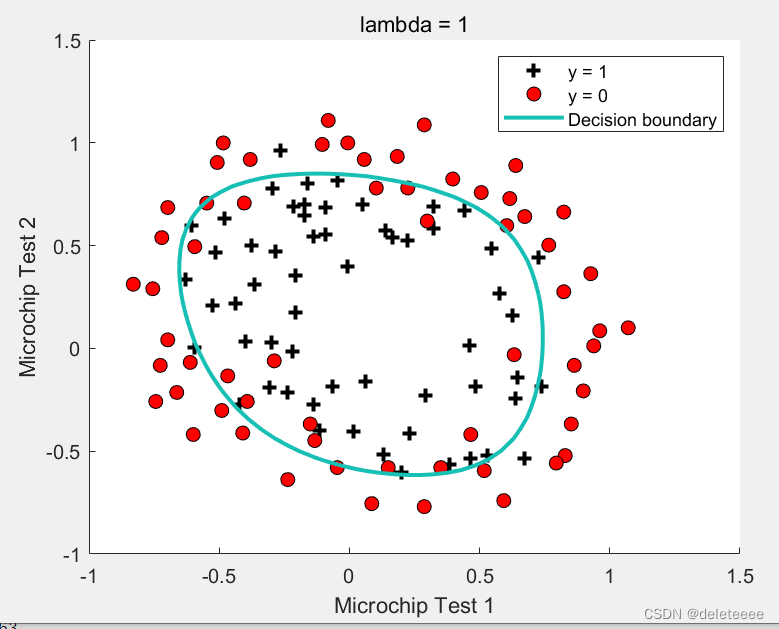
图11 决策边界曲线

可以看出曲线已经基本上将两类样本分开了。

6分类精度

同样通过sigmoid函数寻找值大于等于0.5的判别为1类，否则为0，所得最终训练集精度为

7.探究lambda值的影响

在正则化公式中可以看出lambda值将会对结果造成影响，而上述实验中lambda为1时有清晰的决策边界。接下来尝试改变lambda的值进一步探究

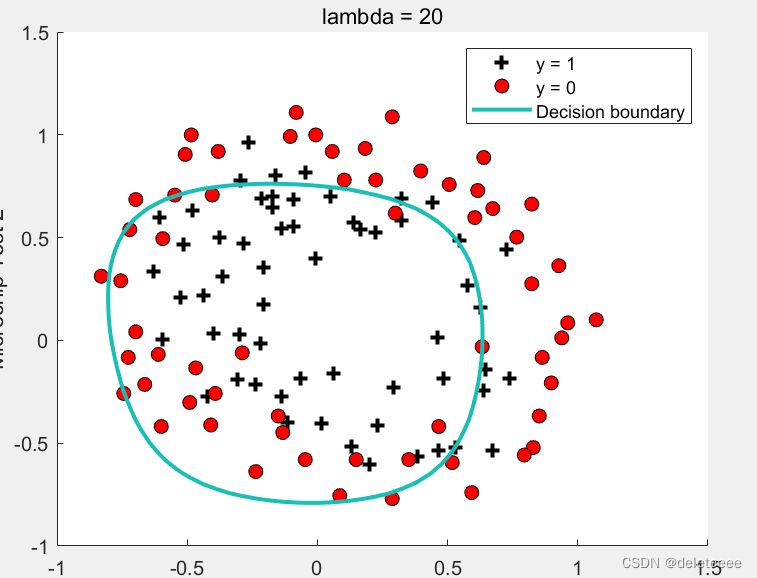
图12 lambda=20

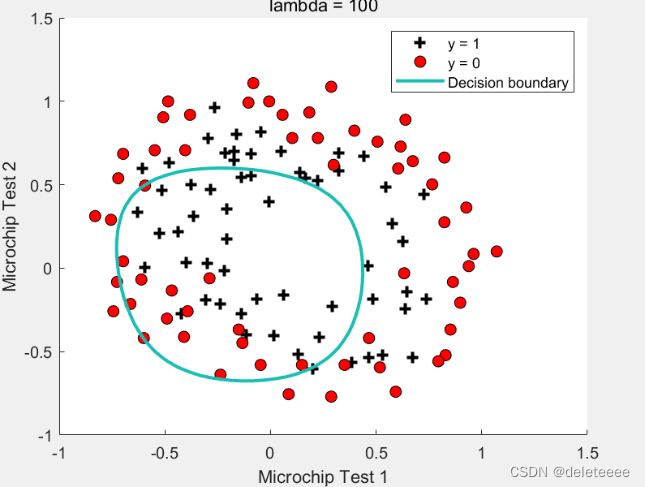
图13 lambda=100

将lambda增大到20或者100后决策线已经不能作为两类的边界了

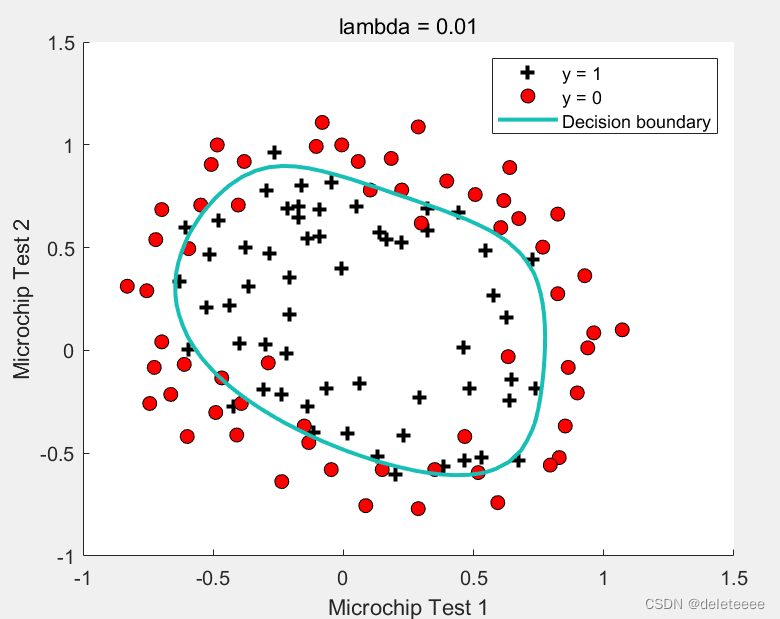
图14 lambda=0.01

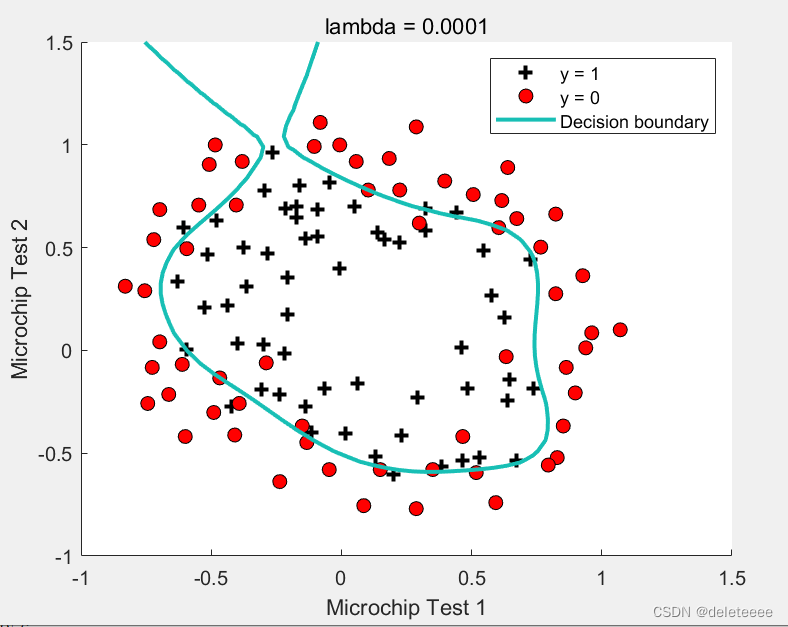
图15 lambda=0.0001

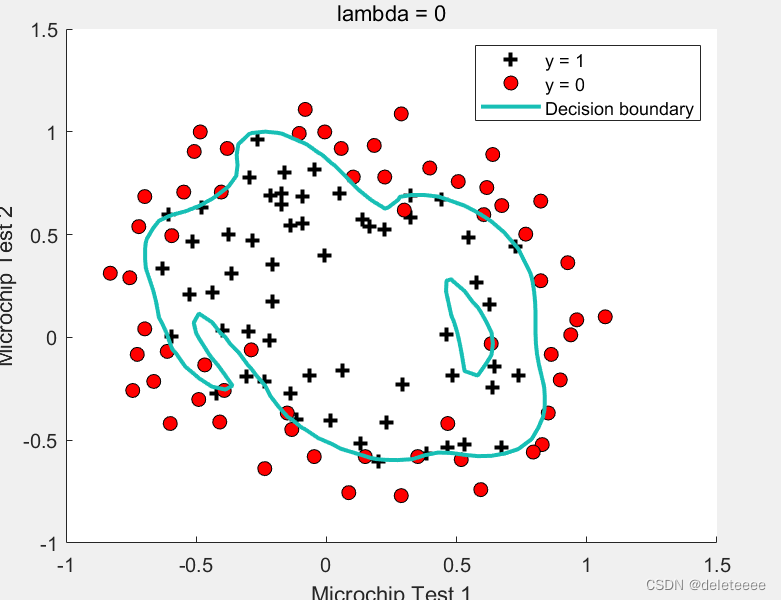
图16 lambda=0

将lambda缩小一定程度如0.01，图像基本没有变换，但是如果继续缩小至0.0001则过度拟合了

四、结果分析

    通过上述实验，我们可以知道在简单的二元分类问题中，我们可以用sigmoid函数作为预测的标准，对数几率回归主要可以用于比较简单的线性判别边界如直线，而对于复杂的判别边界则需要使用正则化logistic回归，将数据升维，从而可以绘制出更复杂的非线性边界，但同时也可能出现欠拟合或过度拟合的问题，正则化参数在这之间起很大的作用，随着lambda的增大拟合程度不断变差，决策边界也不会很好地跟随数据，从而导致数据拟合不足，此时在拟合中theta就会更小，而带来的结果是拟合程度越来越差，正则化约束力过强，当lambda无限大时就完全欠拟合。但是随着L过度减小我们也发现，拟合程度越来越高，lambda的影响降低，正则化约束力不够，带来的结果就是出现过拟合。综上正则化可以防止训练模型的过拟合，从而得到更好的结果。