概念大合集06
- 1、树
- 1.1 树的相关定义
- 1.2 树的基本运算
- 1.3 树的基本术语
- 1.3.1 结点的度,树的度
- 1.3.2 分支结点,叶子节点
- 1.3.3 路径,路径长度
- 1.3.4 孩子结点,双亲结点,兄弟结点
- 1.3.5 结点层次,树的高度
- 1.3.6 有序树,无序树
- 1.3.7 森林
- 1.4 树的性质
- 2、二叉树
- 2.1 二叉树的相关概念
- 2.1.1 二叉树的相关定义
- 2.1.2 二叉树的表现形式
- 2.1.3 满二叉树
- 2.1.4 完全二叉树
- 2.1.5 完全二叉树与满二叉树比较
- 2.2 二叉树的性质
- 2.3 二叉树的构造
- 2.3.1 先序序列
- 2.3.2 中序序列
- 2.3.3 后序序列
- 2.3.4 由遍历序列构造二叉树
阅读指南:
在本文中,我们将重点探讨概念性的内容,旨在为您提供更为流畅和易于理解的阅读体验。关于树和二叉树的算法实现部分,作者已经安排在另一篇文章中进行详细阐述。
本篇文章的相关算法
数据结构大合集06——树与二叉树的相关函数运算算法
1、树
1.1 树的相关定义
树:有n个结点(元素)组成的有限集合(记为T);
空树:当n = 0时;
根结点:n > 0,这n个结点中有且仅有一个结点作为树的根节点,简称为“根”;
子树:除根节点外的m个不相交的有限集,其中每个子集本身又是一颗符合本定义的树,称为根节点的子树;
1.2 树的基本运算
| 函数名 | 函数作用 |
|---|---|
| InitTree(&t) | 初识化树,构造一个空树t |
| DestroyTree(&t) | 销毁树,释放为树t分配的内存空间 |
| TreeHeight (t) | 求树t的高度 |
| Parent(t , p) | 求树t中p所指节点的双亲结点 |
| Brother(t , p) | 求树t中p所指节点的所有兄弟节点 |
| Sonts(t , p) | 求树t中p所指节点的所有子孙节点 |
1.3 树的基本术语
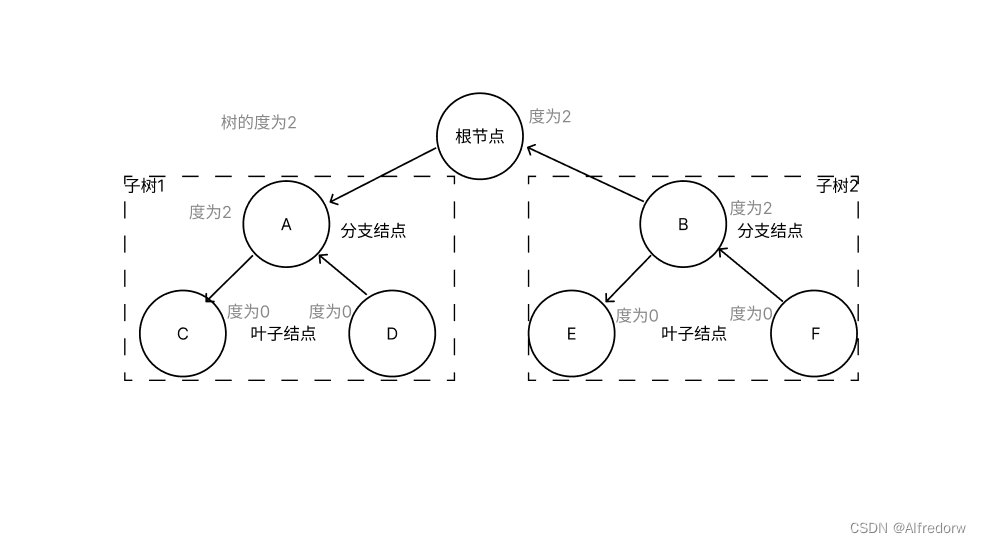
1.3.1 结点的度,树的度
- 结点的度:树中某个结点的子树的个数
- 树的度:所有结点的度中最大值
1.3.2 分支结点,叶子节点
- 分支结点:度不为0的结点非根结点
- 叶子结点:度为0的结点
1.3.3 路径,路径长度
- 路径:对于树中任一两个结点ki和Kj,若速中存在一个结点序列,除kj外的任一结点都是起其在序列中的前一个结点的后继结点,则这段序列成为ki到Kj的一条路径
- 路径长度:路径序列的结数目减1
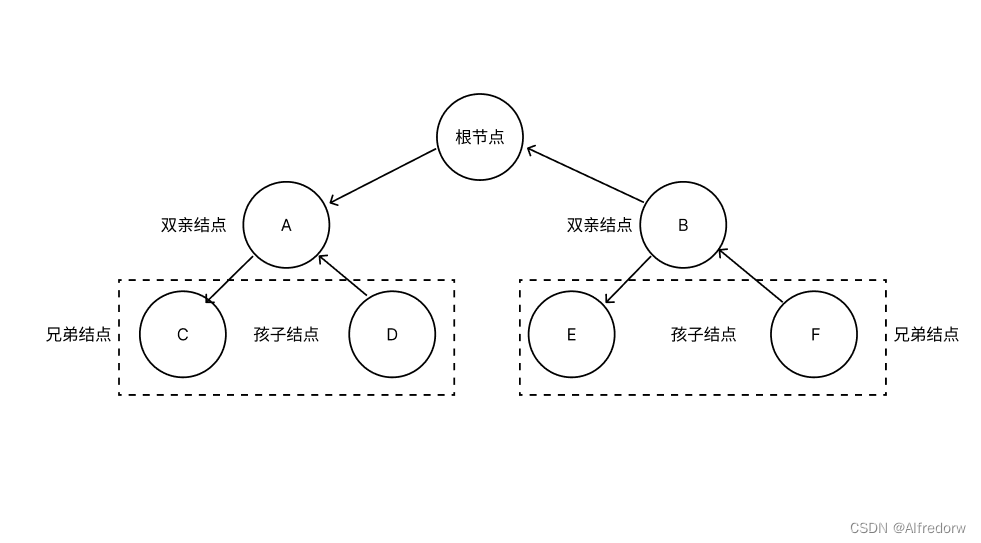
1.3.4 孩子结点,双亲结点,兄弟结点
- 孩子结点:每个结点的后继结点
- 双亲结点:孩子结点的前向节点
- 兄弟结点:具有同一双亲结点的孩子结点互称为兄弟结点
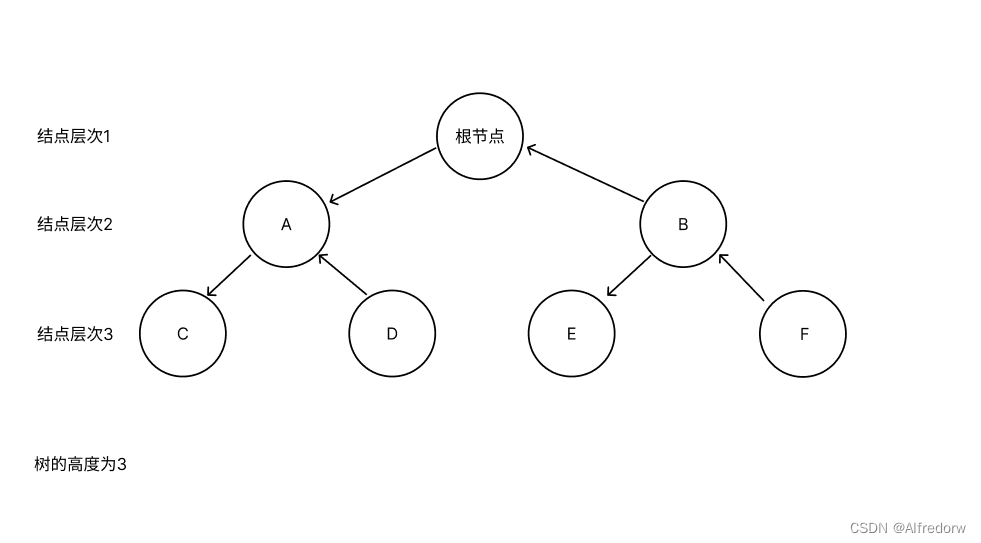
1.3.5 结点层次,树的高度
- 结点层次(结点深度):从根结点开始数起,即根结点为1,依次排列
- 树的高度(树的深度):树中结点的最大层次
1.3.6 有序树,无序树
- 有序树:树中各结点的子树是按照一定的次序从左向右排列的,且相对次序不能随意更换(一般都是有序树)
- 无序树:与有序树相反
1.3.7 森林
- 森林:m棵树互不相交的数的集合,好比一个根结点有多个子树,这时候把根结点删除,于是多个子树就组成了森林
1.4 树的性质
- 树中的结点(元素)数等于所有结点的度数之和加1。
- 度为m的数找那个第i层上最多有mi-1个结点( i > 0 )。
推广:当一个m次树的第i层有mi-1个结点时,则层该层是满的,若每一层都是满的,则称该树为满m次树。
- 高度为h的m次树最多有 (mk - 1) / (m - 1)个结点。
- 具有n个结点的m次树的最小高度为logm(n * (m - 1) + 1)。
注:
具体的推到过程,读者们可以自己尝试尝试,这里就不在过多推导了。
2、二叉树
2.1 二叉树的相关概念
2.1.1 二叉树的相关定义
二叉树:一个有限的结点集合,这个结点或者为空,或者有一个根节点和两颗互不相交的称为左子树与右子树的二叉树组成。
层序编号:约定编号从树根为1开始,按照层数从小到大,同一层从左到右的次序进行。
树中所有的基本术语在二叉树里面都适用。
注:
任何m次树都可以转化为二叉树结构;
2.1.2 二叉树的表现形式
-
空二叉树
-
单个结点的二叉树
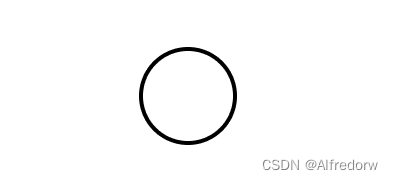
-
右子树为空的二叉树
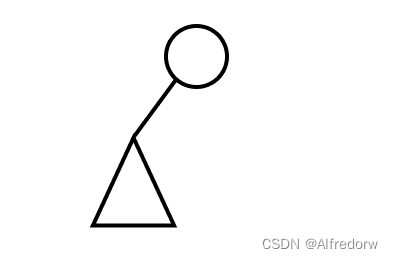
-
左子树为空的二叉树
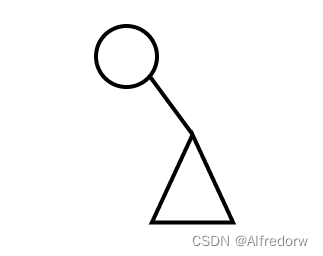
-
左右子树都不为空的二叉树
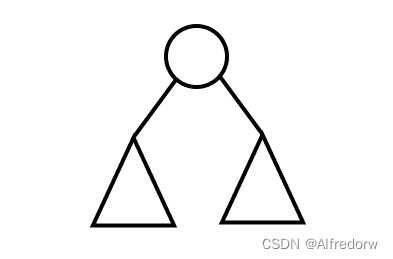
2.1.3 满二叉树
满二叉树:所有分支结点都有左右孩子结点,并且叶子结点都集中在二叉树的最下一层。
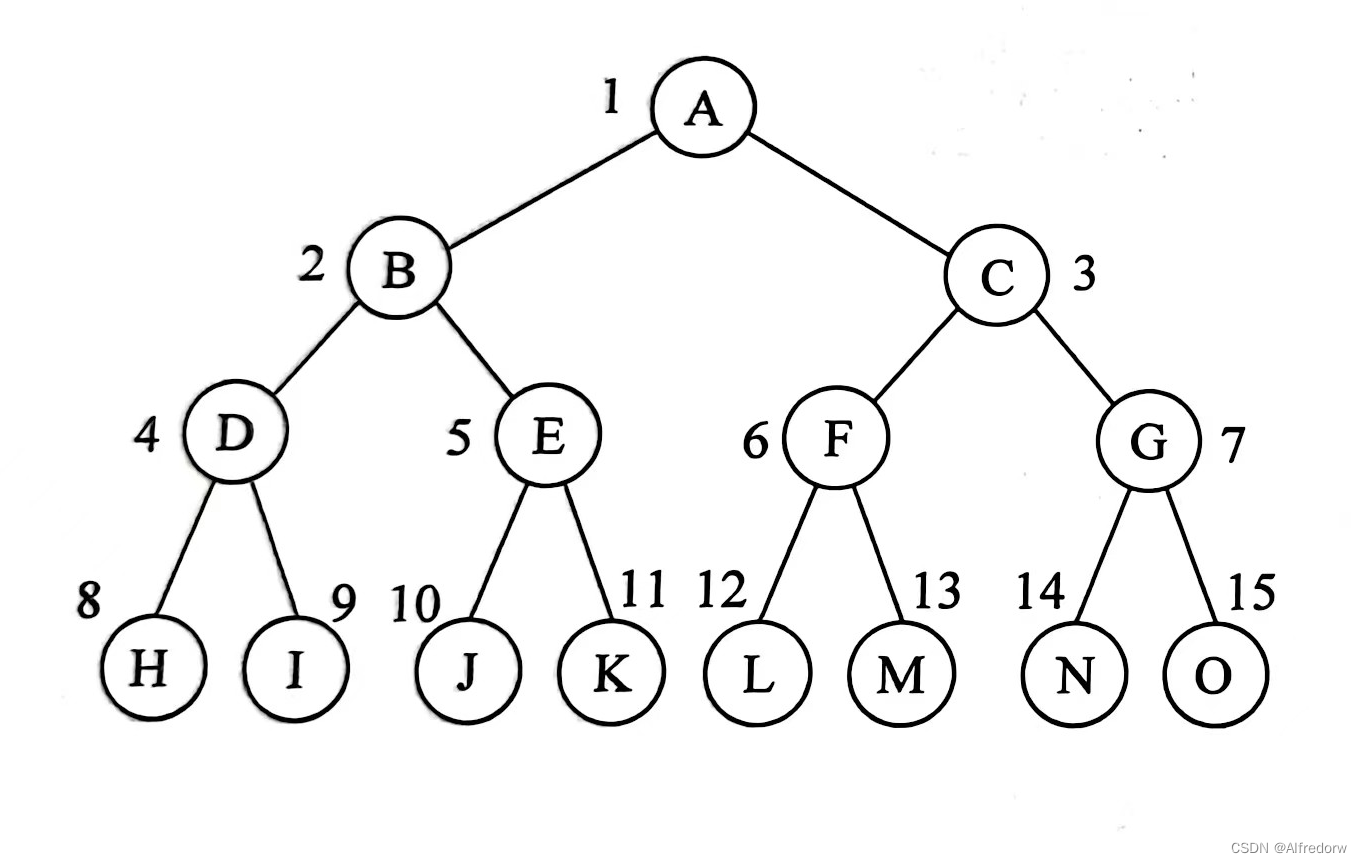
满二叉树在一些特定的数据存储和检索算法中有用,但相对较少见。
满二叉树(非空)的特点:
- 叶子结点都在最下一层
- 只有度为0和度为2的结点
2.1.4 完全二叉树
完全二叉树:二叉树中最多只有最下面两层的结点的度数可以小于2,并且最下面一层的叶子结点都依次排列在该层的最左边的位置上
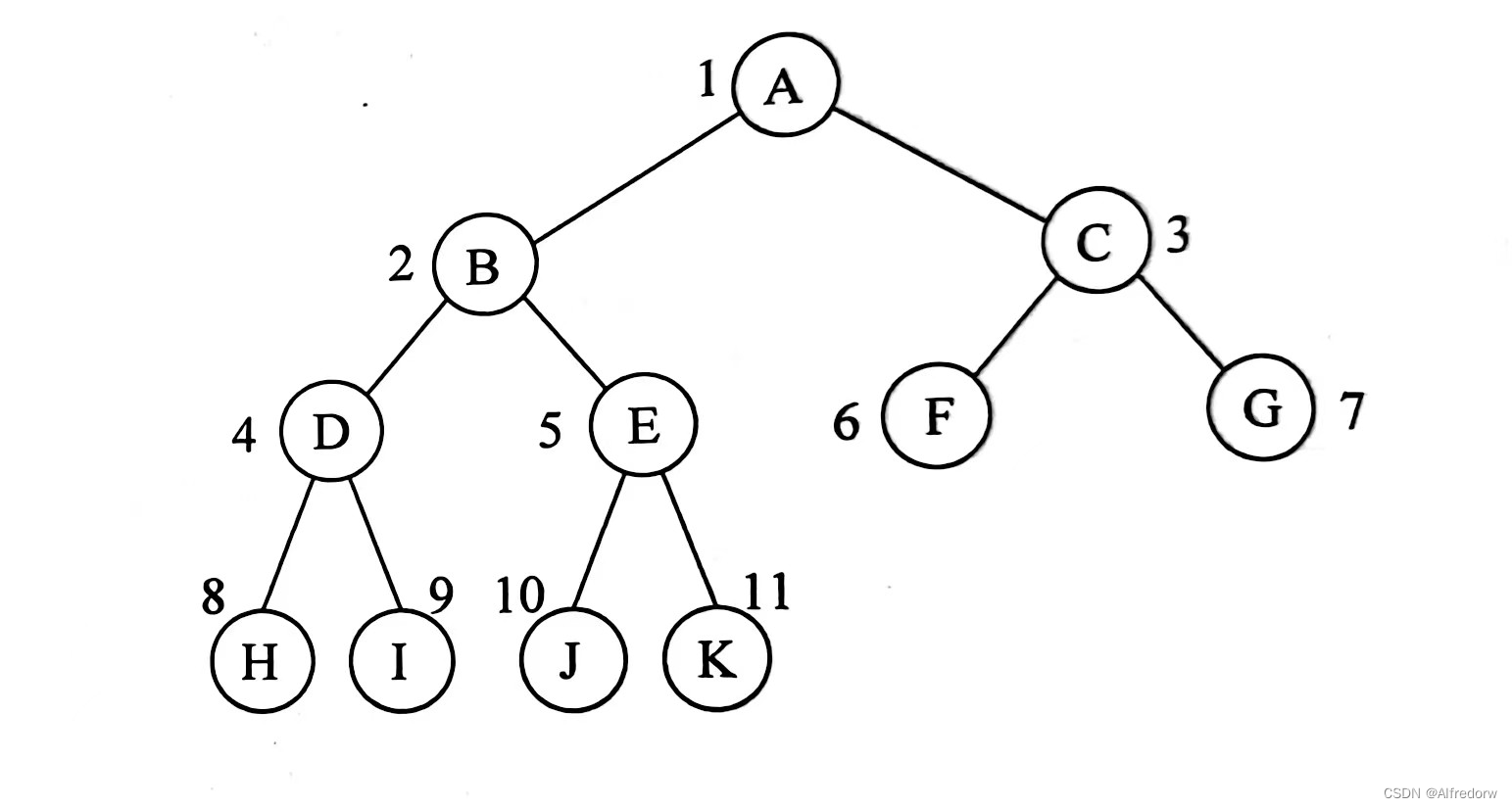
完全二叉树在堆数据结构中广泛应用,如二叉最小堆和二叉最大堆。
完全二叉树(非空)的特点:
- 叶子节点只可能在最下面两层中出现
- 对于最大层次中的叶子结点,都依次排列在该层最左边的位置上
- 如果有度为1的结点,只看有一个,且该结点只有左孩子而无右孩子
- 在按层序编号是,一旦出现编号为i的结点是叶子结点或只有左孩子,则编号大于i的结点均为叶子结点。
- 当结点总数n为奇数时,n1 = 0;当n为偶数时, n1 = 1。
2.1.5 完全二叉树与满二叉树比较
由满二叉树与完全二叉树的表示图可以看出:
满二叉树的成立条件:
每个节点都有两个子节点(除非是叶子节点),并且所有叶子节点都在同一层级。
完全二叉树的成立条件:
每一层都是满的,或者除了最后一层外其他层都是满的,且最后一层的节点尽可能地靠左排列。
当满二叉树的高度与完全二叉树相同时,满二叉树是完全二叉树的一种特殊体现,并且完全二叉树与同高度的满二叉树的对应位置结点的编号相同。
2.2 二叉树的性质
- 非空二叉树上的叶子结点树等于双分子结点数加1。
- 在二叉树的第i层上至多有2i-1个结点( i >= 1 )。
- 深度为h的二叉树至多有2h-1个结点( k >= 1 )。
- 具有n个节点的完全二叉树深为( log2(n + 1) )。
2.3 二叉树的构造
2.3.1 先序序列
沿着二叉树外沿,逆时针走一圈回到根节点,路上遇到的元素顺序,就是先序遍历的结果
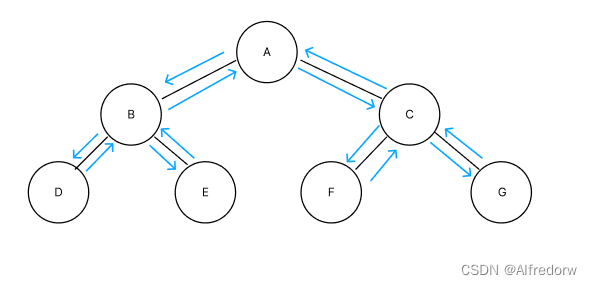
先序遍历结果为:A B D E C F G
2.3.2 中序序列
中序遍历可以看成,二叉树每个节点,垂直方向投影下来(可以理解为每个节点从最左边开始垂直掉到地上),然后从左往右数,得出的结果便是中序遍历的结果
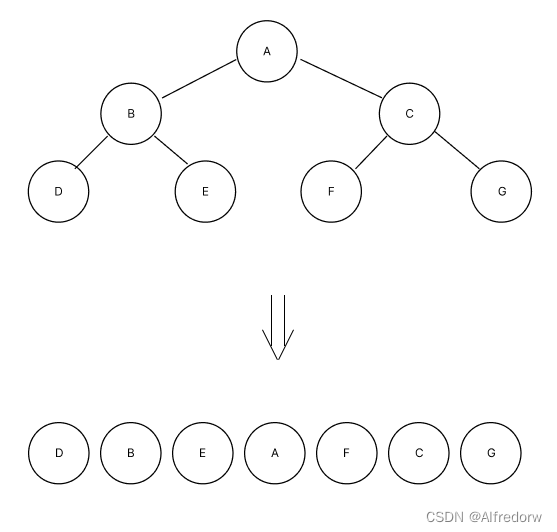
中遍历结果为:D B E A F C G
2.3.3 后序序列
后序遍历就像是剪葡萄,我们要把一串葡萄剪成一颗一颗的。
围着树的外围绕一圈,如果发现一剪刀就能剪下的葡萄(必须是一颗葡萄)(也就是葡萄要一个一个掉下来,不能一口气掉超过1个这样),就把它剪下来,组成的就是后序遍历了。
后序遍历中,根节点默认最后面
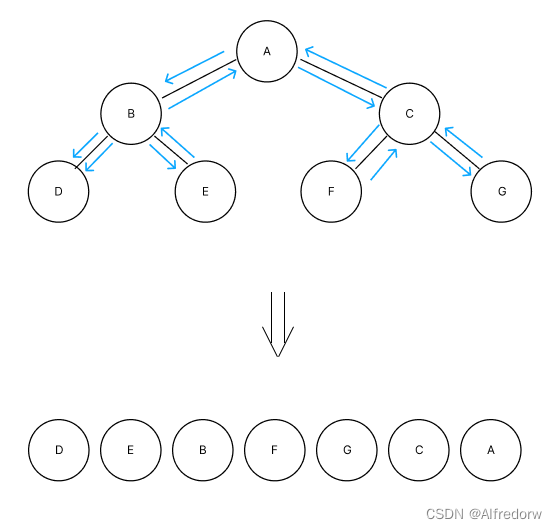
后序遍历结果:H I D J E B K F G C A
2.3.4 由遍历序列构造二叉树
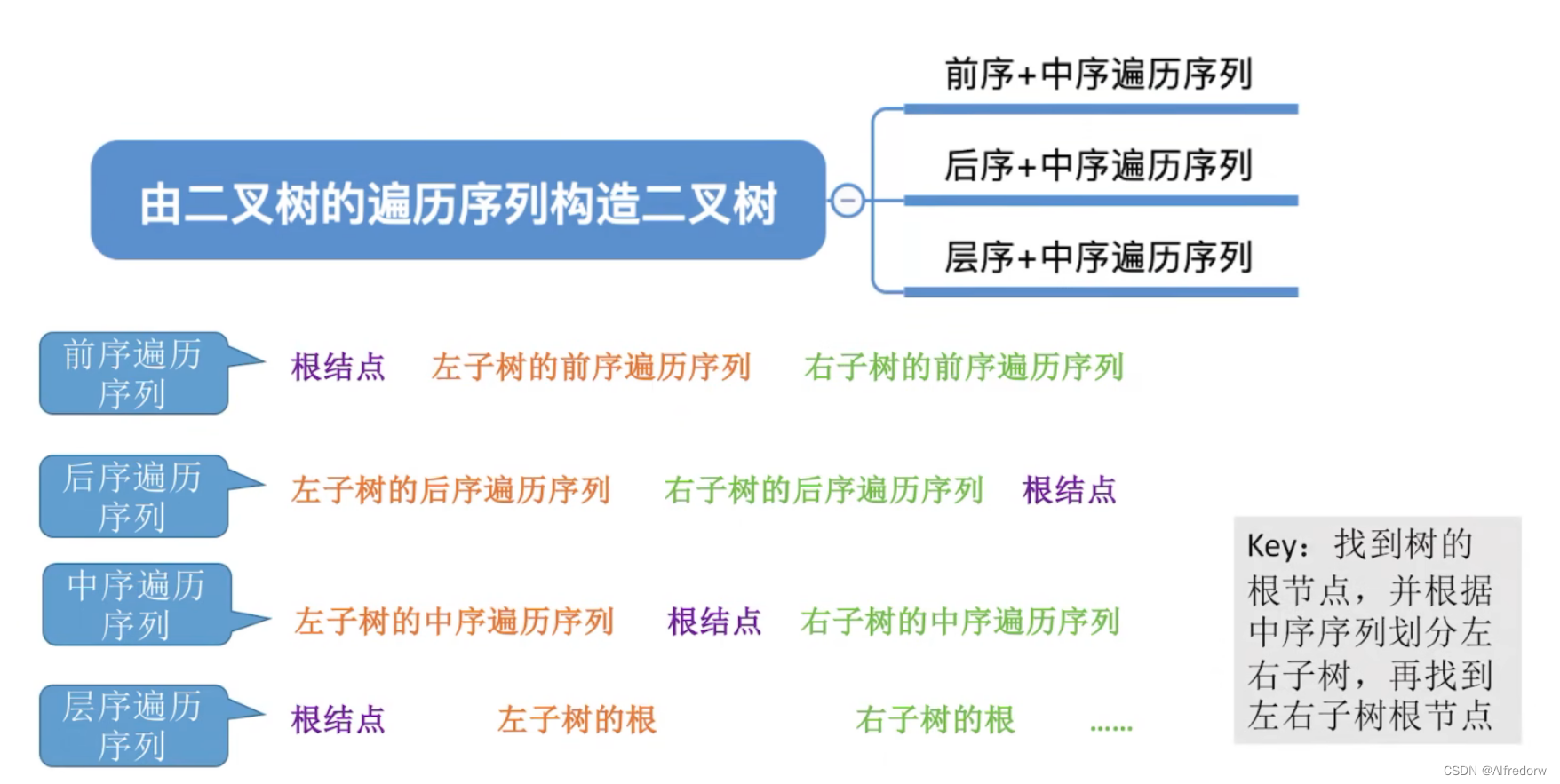
本篇文章的相关算法
数据结构大合集06——树与二叉树的相关函数运算算法
上一篇文章
数据结构的概念大合集05(串)