“啤酒和尿布的荣誉”
概念
- 项 item:单个的事物个体 ,I={i1,i2…im}是所有项的集合,|I|=m是项的总数
- 项集(item set)/模式(pattern):项的集合,包含k个项的项集称为k-项集
- 数据集(data set)/数据库(data base):D={T1,T2,…Tn}是与任务相关的数据库事务/记录/交易的集合,每个事务有一个标识符,称作TID。|D|=n为数据集中包含的事务总数。
- 支持度support :项集的出现频率(0~1)/比例(绝对数)
- 置信度/可信度(confidence):在D中的那些包含A的事务中,B也同时出现的条件概率P(B|A)=P(AB)/P(A)
- 频繁项集(frequent itemset)/模式(pattern):项集的支持度>=最小支持度(min support)
- 关联规则(association rules):关联规则是形如A=>B的蕴含式,具有支持度s=support(A ∪ \cup ∪B),c=confidence(A=>B)=P(B|A)=support(A ∪ \cup ∪B)/support(A)
- 强规则:同时满足最小支持度和最小置信度的规则称作强规则。关联规则发掘分为两步:
- 找出所有频繁项集
- 产生强规则
例子
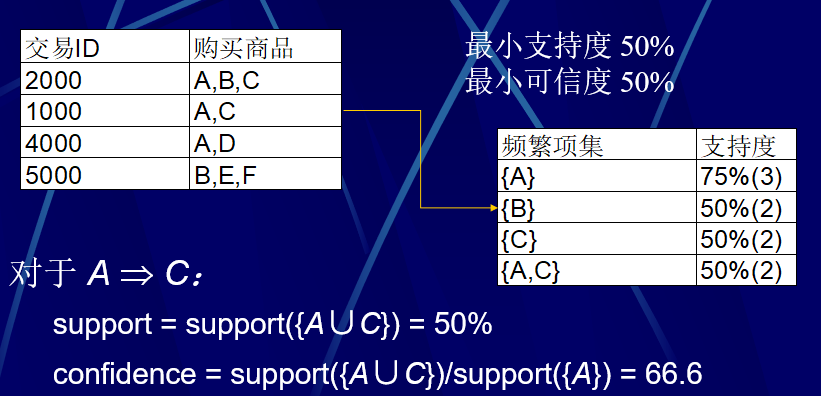
结论与注意事项
1.非频繁项集的超集都是非频繁的
support(y)<=support(x)<min_sup
y=x
∪
\cup
∪其他
2.频繁项集的子集是频繁的
1.强规则不一定有价值
2.相关分析:corr(A,B)=P(A
∪
\cup
∪B)/P(A)P(B)
正相关>1,负相关<1,独立=1
问题分类
根据规则中所处理的值的类型分类:
- 布尔关联规则(boolean association rule):规则考虑的关联是项的在与不在
- 量化关联规则(quantitative association rule):规则描述的是量化的项或属性之间的关联
根据规则中所涉及的数据维数分类:
- 单维关联规则(single-dimensional association rule) :规则中的项或属性每个只涉及一个维
- 多维关联规则(multi-dimensional association rule):规则涉及多维度
根据规则中所涉及的抽象层分类:
- 单层关联规则(single-level association rule):规则不考虑项的分层
- 多层关联规则(multi-level association rule):考虑项的分层 buys(X,milk)=>buys(X,food)
频繁模式挖掘的分类:
- 频繁模式挖掘
- 交互挖掘
- 增量挖掘
- 效用频繁模式挖掘
- 最大频繁模式挖掘
- 频繁闭合模式挖掘
- 并行/分布式挖掘
经典算法
基于候选项生成与测试(candidate generation and test)
非频繁项集的超集都是非频繁的
代表作:apriori(1994)
基于分治的模式增长(pattern growth)
采用分而治之的方法:频繁项集的子集是频繁的
代表作:FP-growth(2000)