( A, B )---1*30*2---( 1, 0 )( 0, 1 )
让网络的输入只有1个节点,AB各由9张二值化的图片组成,排列组合A和B的所有可能性,固定收敛误差为7e-4,统计收敛迭代次数,并比较迭代次数的变化规律。
| 差值结构 | A-B | 迭代次数 | 等位点数值差 | 复合差 | ||||||||
| 0 | 0 | 0 | 1b | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*0*1*1*1*1*1*1 | 23674.65 | 6 | 6 |
如0*0*0*0*0*0*0*0*0与0*0*0*1*1*1*1*1*1分类收敛误差为7e-4时,收敛199次,平均迭代次数为23674.65。
统计差值结构中6个1,3个0的情况,也就是以1为底,0在1中的分布情况,共得到10组差值结构
| 差值结构 | A-B | 迭代次数 | 等位点数值差 | 复合差 | ||||||||
| 0 | 0 | 0 | 1b | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*0*1*1*1*1*1*1 | 23674.65 | 6 | 6 |
| 0 | 0 | 1b | 1b | 1b | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-0*0*1*1*1*1*1*0*1 | 24600.06 | 6 | 6+g1 |
| 0 | 0 | 1b | 0 | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*1*0*1*1*1*1*1 | 25376.7 | 6 | 6+g2 |
| 0 | 0 | 1b | 1b | 1b | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*1*1*1*1*0*1*1 | 25430.23 | 6 | 6+g3 |
| 0 | 0 | 1b | 1b | 1b | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*1*1*1*0*1*1*1 | 26199.71 | 6 | 6+g4 |
| 0 | 1b | 0 | 1b | 0 | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*0*1*0*1*1*1*1 | 26363.37 | 6 | 6+g5 |
| 0 | 0 | 1b | 1b | 0 | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*1*1*0*1*1*1*1 | 26679.47 | 6 | 6+g6 |
| 0 | 1b | 0 | 1b | 1b | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*0*1*1*1*0*1*1 | 27187.91 | 6 | 6+g7 |
| 0 | 1b | 0 | 1b | 1b | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*0*1*1*0*1*1*1 | 27705.84 | 6 | 6+g8 |
| 0 | 1b | 1b | 0 | 1b | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*0*1*1*0*1*1 | 28649.06 | 6 | 6+g9 |
这10组数据迭代次数依次变大
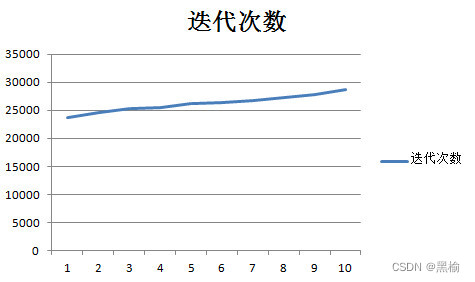
这10组的等位点数值差都是6,因此有理由认为迭代次数的大小取决于这6个1和3个0的分布。特别直观的是6和6+g9这两组
| 复合差 | 差值结构 | ||||||||
| 6 | 0 | 0 | 0 | 1b | 1b | 1b | 1b | 1b | 1b |
| 6+g9 | 0 | 1b | 1b | 0 | 1b | 1b | 0 | 1b | 1b |
显然对于6这组,3个0和6个1无间隔的分布在一起,而6+g9这组,6个1以2+2+2的形式等距分布,6+g9分布的散度要大于6。
如果认为6到6+g9的变化暗示了这10组数据散度越来越大的变化规律,有几组数据变得很难解释6+g1/6+g2,6+g3/6+g6,6+g7/6+g8,这几组数据之间是镜像对称的,分布完全相同,仅仅是顺序不同,但迭代次数并不相同。
| 6+g1 | 0 | 0 | 1b | 1b | 1b | 1b | 1b | 0 | 1b |
| 6+g2 | 0 | 0 | 1b | 0 | 1b | 1b | 1b | 1b | 1b |
比如6+g1和6+g2,6个b1按照5+1的结构分布,差别是6+g1为00向右侧为5+1,而6+g2为00向右侧为1+5.仅仅因为这个顺序的差异6+g2的迭代次数要大于6+g1。
更为明显的是6+g3和6+g6
| 6+g3 | 0 | 0 | 1b | 1b | 1b | 1b | 0 | 1b | 1b |
| 6+g4 | 0 | 0 | 1b | 1b | 1b | 0 | 1b | 1b | 1b |
| 6+g5 | 0 | 1b | 0 | 1b | 0 | 1b | 1b | 1b | 1b |
| 6+g6 | 0 | 0 | 1b | 1b | 0 | 1b | 1b | 1b | 1b |
这两组b1是按照2+4的结构分布,区别是6+g3向右侧为4+2而6+g6向右侧为2+4.而g3和g6之间还有g4和g5两个梯度.
如果认为g3到g6之间的变化也是按照散度越来越大的方向在变化,就只能认为这个散度和进样顺序是有关系的,如果要考虑顺序就意味着这个散度不是静态的,还要考虑这个结构本身的构造过程。
所以如果等位点数值差和散度共同决定了迭代次数,那散度应该是含时的。
| 差值结构 | A-B | 迭代次数 | 等位点数值差 | 复合差 | ||||||||
| 1b | 1b | 1b | 0 | 0 | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*1*1*0*0*0*1*1*1 | 23577.27 | 6 | 6 |
| 1b | 1b | 1b | 1b | 1b | 1b | 0 | 0 | 0 | 0*0*0*0*0*0*0*0*0-1*1*1*1*1*1*0*0*0 | 23610.85 | 6 | 6 |
| 1b | 1b | 1b | 1b | 0 | 0 | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*1*1*1*0*0*0*1*1 | 23630.1 | 6 | 6 |
| 0 | 0 | 0 | 1b | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*0*1*1*1*1*1*1 | 23674.65 | 6 | 6 |
| 1b | 1b | 1b | 1b | 1b | 0 | 0 | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*1*1*1*1*0*0*0*1 | 23676.15 | 6 | 6 |
| 0 | 0 | 1b | 1b | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-0*0*1*1*1*1*1*1*0 | 23680.7 | 6 | 6 |
| 1b | 1b | 0 | 0 | 0 | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*1*0*0*0*1*1*1*1 | 23742.06 | 6 | 6 |
| 1b | 0 | 0 | 0 | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*0*0*0*1*1*1*1*1 | 23770.09 | 6 | 6 |
| 0 | 1b | 1b | 1b | 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0*0*0*0*0-0*1*1*1*1*1*1*0*0 | 23796.38 | 6 | 6 |
| 1b | 1b | 0 | 1b | 0 | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*1*0*1*0*0*1*1*1 | 24568.98 | 6 | 6+g1 |
| 1b | 1b | 1b | 1b | 0 | 1b | 0 | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*1*1*1*0*1*0*0*1 | 24587.37 | 6 | 6+g1 |
| 0 | 0 | 1b | 1b | 1b | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-0*0*1*1*1*1*1*0*1 | 24600.06 | 6 | 6+g1 |
| 0 | 1b | 0 | 0 | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*0*0*1*1*1*1*1 | 24637.17 | 6 | 6+g1 |
| 1b | 1b | 1b | 1b | 1b | 0 | 1b | 0 | 0 | 0*0*0*0*0*0*0*0*0-1*1*1*1*1*0*1*0*0 | 24640.92 | 6 | 6+g1 |
| 0 | 1b | 1b | 1b | 1b | 1b | 0 | 1b | 0 | 0*0*0*0*0*0*0*0*0-0*1*1*1*1*1*0*1*0 | 24647.18 | 6 | 6+g1 |
| 1b | 0 | 1b | 0 | 0 | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*0*1*0*0*1*1*1*1 | 24672.09 | 6 | 6+g1 |
| 1b | 1b | 1b | 0 | 1b | 0 | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*1*1*0*1*0*0*1*1 | 24675.73 | 6 | 6+g1 |
| 1b | 0 | 0 | 1b | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*0*0*1*1*1*1*1*0 | 24713.77 | 6 | 6+g1 |
| 1b | 1b | 1b | 0 | 0 | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*1*1*0*0*1*0*1*1 | 25261.68 | 6 | 6+g2 |
| 1b | 0 | 1b | 1b | 0 | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*0*1*1*0*0*1*1*1 | 25327.43 | 6 | 6+g3 |
| 1b | 1b | 1b | 1b | 1b | 0 | 0 | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*1*1*1*1*0*0*1*0 | 25372.77 | 6 | 6+g2 |
| 0 | 0 | 1b | 0 | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*1*0*1*1*1*1*1 | 25376.7 | 6 | 6+g2 |
| 1b | 1b | 1b | 1b | 0 | 0 | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*1*1*1*0*0*1*0*1 | 25387.78 | 6 | 6+g2 |
| 1b | 1b | 0 | 0 | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*1*0*0*1*1*1*1*0 | 25390.54 | 6 | 6+g3 |
| 1b | 0 | 1b | 1b | 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0*0*0*0*0-1*0*1*1*1*1*1*0*0 | 25406.26 | 6 | 6+g2 |
| 0 | 1b | 1b | 1b | 1b | 1b | 0 | 0 | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*1*1*1*0*0*1 | 25428.86 | 6 | 6+g2 |
| 0 | 0 | 1b | 1b | 1b | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*1*1*1*1*0*1*1 | 25430.23 | 6 | 6+g3 |
| 1b | 1b | 1b | 0 | 1b | 1b | 0 | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*1*1*0*1*1*0*0*1 | 25444.67 | 6 | 6+g3 |
| 1b | 0 | 0 | 1b | 0 | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*0*0*1*0*1*1*1*1 | 25447.99 | 6 | 6+g2 |
| 1b | 1b | 1b | 1b | 0 | 1b | 1b | 0 | 0 | 0*0*0*0*0*0*0*0*0-1*1*1*1*0*1*1*0*0 | 25449.66 | 6 | 6+g3 |
| 1b | 0 | 0 | 1b | 1b | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*0*0*1*1*1*1*0*1 | 25465.07 | 6 | 6+g3 |
| 0 | 1b | 1b | 1b | 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-0*1*1*1*1*0*1*1*0 | 25472.1 | 6 | 6+g3 |
| 1b | 1b | 0 | 0 | 1b | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*1*0*0*1*0*1*1*1 | 25481.92 | 6 | 6+g2 |
| 0 | 1b | 0 | 1b | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-0*1*0*1*1*1*1*1*0 | 25528.2 | 6 | 6+g2 |
| 1b | 1b | 0 | 1b | 1b | 0 | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*1*0*1*1*0*0*1*1 | 25578.44 | 6 | 6+g3 |
| 0 | 1b | 1b | 0 | 0 | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*0*0*1*1*1*1 | 25616.86 | 6 | 6+g3 |
| 1b | 0 | 0 | 1b | 1b | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*0*0*1*1*1*0*1*1 | 25990.68 | 6 | 6+g4 |
| 1b | 1b | 0 | 0 | 1b | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*1*0*0*1*1*1*0*1 | 26028.41 | 6 | 6+g4 |
| 1b | 1b | 1b | 0 | 0 | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*1*1*0*0*1*1*1*0 | 26070.84 | 6 | 6+g4 |
| 0 | 1b | 1b | 1b | 0 | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-0*1*1*1*0*1*1*1*0 | 26084.1 | 6 | 6+g4 |
| 1b | 0 | 1b | 1b | 1b | 0 | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*0*1*1*1*0*0*1*1 | 26109.04 | 6 | 6+g4 |
| 0 | 1b | 1b | 1b | 0 | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*1*0*0*1*1*1 | 26127.84 | 6 | 6+g4 |
| 1b | 1b | 1b | 0 | 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0*0*0*0*0-1*1*1*0*1*1*1*0*0 | 26147.23 | 6 | 6+g4 |
| 1b | 1b | 0 | 1b | 1b | 1b | 0 | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*1*0*1*1*1*0*0*1 | 26193.08 | 6 | 6+g4 |
| 0 | 0 | 1b | 1b | 1b | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*1*1*1*0*1*1*1 | 26199.71 | 6 | 6+g4 |
| 1b | 0 | 1b | 0 | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*0*1*0*1*1*1*1*0 | 26304.74 | 6 | 6+g5 |
| 0 | 1b | 0 | 1b | 1b | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-0*1*0*1*1*1*1*0*1 | 26314.14 | 6 | 6+g5 |
| 1b | 1b | 0 | 1b | 0 | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*1*0*1*0*1*0*1*1 | 26328.38 | 6 | 6+g5 |
| 0 | 1b | 1b | 1b | 1b | 0 | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*1*1*0*1*0*1 | 26337.1 | 6 | 6+g5 |
| 1b | 1b | 1b | 0 | 1b | 0 | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*1*1*0*1*0*1*0*1 | 26344.58 | 6 | 6+g5 |
| 0 | 1b | 0 | 1b | 0 | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*0*1*0*1*1*1*1 | 26363.37 | 6 | 6+g5 |
| 1b | 1b | 1b | 1b | 0 | 1b | 0 | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*1*1*1*0*1*0*1*0 | 26366.21 | 6 | 6+g5 |
| 1b | 0 | 1b | 0 | 1b | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*0*1*0*1*0*1*1*1 | 26367.81 | 6 | 6+g5 |
| 1b | 0 | 1b | 1b | 1b | 1b | 0 | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*0*1*1*1*1*0*1*0 | 26419.96 | 6 | 6+g5 |
| 1b | 1b | 0 | 1b | 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0*0*0*0*0-1*1*0*1*1*1*1*0*0 | 26524.32 | 6 | 6+g6 |
| 1b | 1b | 1b | 0 | 0 | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*1*1*0*0*1*1*0*1 | 26589.14 | 6 | 6+g6 |
| 1b | 1b | 1b | 1b | 0 | 0 | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*1*1*1*0*0*1*1*0 | 26605.88 | 6 | 6+g6 |
| 1b | 0 | 0 | 1b | 1b | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*0*0*1*1*0*1*1*1 | 26609.56 | 6 | 6+g6 |
| 0 | 1b | 1b | 0 | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-0*1*1*0*1*1*1*1*0 | 26624.01 | 6 | 6+g6 |
| 1b | 0 | 1b | 1b | 1b | 1b | 0 | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*0*1*1*1*1*0*0*1 | 26657.91 | 6 | 6+g6 |
| 0 | 0 | 1b | 1b | 0 | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*0*1*1*0*1*1*1*1 | 26679.47 | 6 | 6+g6 |
| 0 | 1b | 1b | 1b | 1b | 0 | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*1*1*0*0*1*1 | 26699.87 | 6 | 6+g6 |
| 1b | 1b | 0 | 0 | 1b | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*1*0*0*1*1*0*1*1 | 26709.34 | 6 | 6+g6 |
| 1b | 0 | 1b | 1b | 0 | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*0*1*1*0*1*0*1*1 | 27012.74 | 6 | 6+g7 |
| 0 | 1b | 1b | 1b | 0 | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*1*0*1*1*0*1 | 27072.65 | 6 | 6+g7 |
| 1b | 1b | 1b | 0 | 1b | 1b | 0 | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*1*1*0*1*1*0*1*0 | 27087.48 | 6 | 6+g7 |
| 0 | 1b | 1b | 0 | 1b | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*0*1*0*1*1*1 | 27089.8 | 6 | 6+g7 |
| 1b | 0 | 1b | 0 | 1b | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*0*1*0*1*1*1*0*1 | 27117.1 | 6 | 6+g7 |
| 1b | 0 | 1b | 1b | 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*0*1*1*1*0*1*1*0 | 27129.56 | 6 | 6+g7 |
| 1b | 1b | 0 | 1b | 1b | 0 | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*1*0*1*1*0*1*0*1 | 27139.84 | 6 | 6+g7 |
| 1b | 1b | 0 | 1b | 0 | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*1*0*1*0*1*1*1*0 | 27139.99 | 6 | 6+g7 |
| 0 | 1b | 0 | 1b | 1b | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*0*1*1*1*0*1*1 | 27187.91 | 6 | 6+g7 |
| 1b | 0 | 1b | 1b | 1b | 0 | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*0*1*1*1*0*1*0*1 | 27529.87 | 6 | 6+g8 |
| 1b | 1b | 0 | 1b | 1b | 1b | 0 | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*1*0*1*1*1*0*1*0 | 27580.35 | 6 | 6+g8 |
| 1b | 0 | 1b | 1b | 0 | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*0*1*1*0*1*1*1*0 | 27610.22 | 6 | 6+g8 |
| 1b | 0 | 1b | 0 | 1b | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-1*0*1*0*1*1*0*1*1 | 27652.75 | 6 | 6+g8 |
| 1b | 1b | 0 | 1b | 0 | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*1*0*1*0*1*1*0*1 | 27669.77 | 6 | 6+g8 |
| 0 | 1b | 1b | 1b | 0 | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*1*0*1*0*1*1 | 27684.17 | 6 | 6+g8 |
| 0 | 1b | 0 | 1b | 1b | 0 | 1b | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*0*1*1*0*1*1*1 | 27705.84 | 6 | 6+g8 |
| 1b | 1b | 1b | 0 | 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*1*1*0*1*0*1*1*0 | 27710.03 | 6 | 6+g8 |
| 0 | 1b | 1b | 0 | 1b | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*0*1*1*1*0*1 | 27755.75 | 6 | 6+g8 |
| 1b | 1b | 0 | 1b | 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0*0*0*0*0-1*1*0*1*1*0*1*1*0 | 28570.65 | 6 | 6+g9 |
| 0 | 1b | 1b | 0 | 1b | 1b | 0 | 1b | 1b | 0*0*0*0*0*0*0*0*0-0*1*1*0*1*1*0*1*1 | 28649.06 | 6 | 6+g9 |
| 1b | 0 | 1b | 1b | 0 | 1b | 1b | 0 | 1b | 0*0*0*0*0*0*0*0*0-1*0*1*1*0*1*1*0*1 | 28701.08 | 6 | 6+g9 |