文章目录
一、堆排序的概念
1、1 堆的基本概念
1、2 堆的特性
二、堆排序的思路及代码实现
2、1 建堆
2、2 向下调整算法详解
2、3 建完堆后进行堆排序
2、3、1 排升序建大堆
2、3、2 建大堆后进行堆排序
三、堆排序的例题
2、1 例题1:堆排序
2、2 例题2:模拟堆
四、总结
标题:重点算法排序之堆排序(下篇)
作者:@Ggggggtm
寄语:与其忙着诉苦,不如低头赶路,奋路前行,终将遇到一番好风景
我们已经讲述了快速排序和归并排序,快速排序和归并排序详解文章链接:重点算法排序之快速排序、归并排序(上篇),我们本篇文章来详细讲述以下堆排序。堆排序的主要内容有:最大堆(大顶堆)、最小堆(小顶堆)、通过孩子找父亲、通过父亲找孩子、向下调整算法建堆。下面我会给大家一一介绍。
一、堆排序的概念
1、1 堆的基本概念
堆一般指的是二叉堆,顾名思义,二叉堆是完全二叉树或者近似完全二叉树。
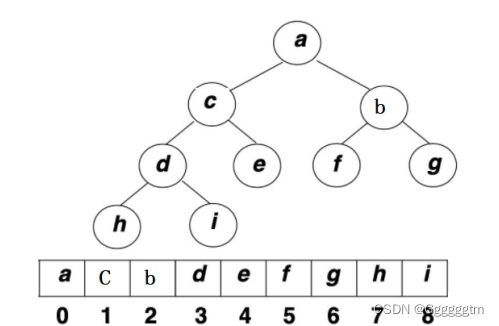
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。 我们是用一个数组来表示一个堆。如下图:
1、2 堆的特性
堆的特性有如下几点:
- 堆是一棵完全二叉树。
- 每个父亲节点的值都大于或等于其子节点的值,为最大堆;反之为最小堆。
- 下标为 i 的结点的父结点下标为(i-1)/2。
- 其下标为i的左右子结点分别为 (2i + 1)、(2i + 2)。
我们上述的后两点讲述了通过孩子找父亲、通过父亲找孩子的方法。那么给出一个乱序的数组,我们怎么建出来一个堆呢?我们接着往下看。
二、堆排序的思路及代码实现
2、1 建堆
我们想用堆对数组进行排序,我们得首先有一个堆。那么问题来了,当给出我们一个乱序的数组时,我们怎么建出一个堆呢?这里就用到了我们的向下调整算法。
2、2 向下调整算法详解
我们在这里用小堆来讲述向下调整算法的实现。那到底什么是向下调整算法呢?我们先看一下向下调整算法的概念。
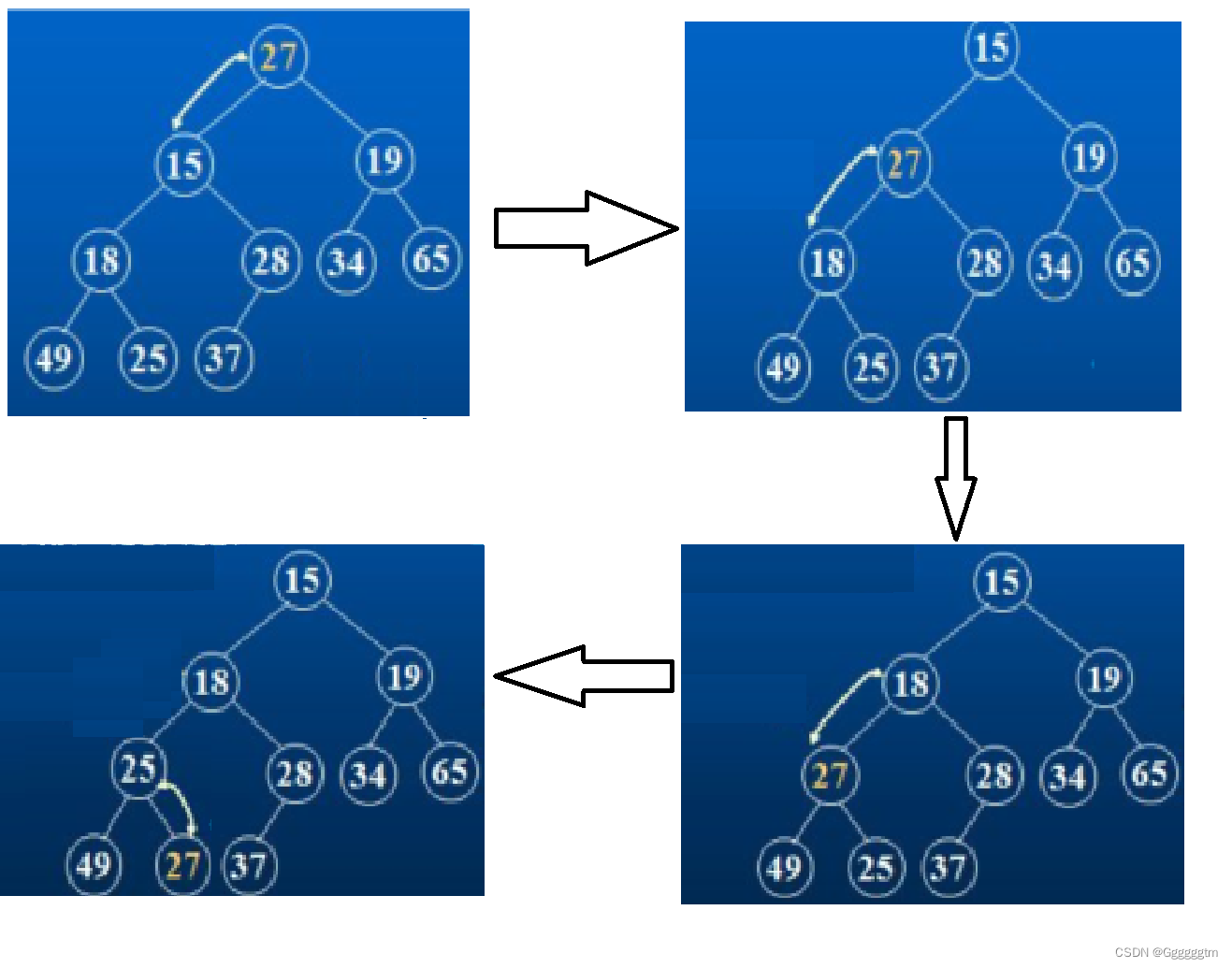
向下调整算法:就是调整结点的位置,使调整的路径上满足大堆或小堆的条件,以调整小堆为例,对某一结点为根结点的堆进行向下调整,首先找到两个子结点中最小的那一个结点,然后与根结点进行比较,如果比根结点小,则交换,交换后使新的根结点为被交换结点的位置,对此位置所在结点继续进行相同的比较与交换,直到调整的结点不在堆的合法范围内或子结点没有比根结点小为止,此时这样的一个过程就叫做向下调整,因为它调整的方向是向下的。我们具体看一个例子。如下图:
注意:建小堆用向下调整算法用的前提为左子树和右子树均为小堆。建大堆同理。
我们看一下向下调整算法的代码实现,如下:
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustDown(int arr[], int n, int root)
{
int parent = root;
int child = parent * 2 + 1;//默认左孩子
while (child < n)
{
if (child+1<n && arr[child + 1] > arr[child])//要考虑到有孩子存在不
{
child += 1;
}
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}那要是左右子树不是小堆呢?如下图:
我们看到上述的完全二叉树并不是一个堆,我们想要对第一个元素3进行向下调整算法,但是3的左右子树并不是小堆,那对3就不能用向下调整算法了。怎么办呢?我们不妨从最后的一颗子树开始使用向下调整算法。 也就是从8开始,依次往前使用向下调整算法即可。
我们再看建堆的整个代码:
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustDown(int arr[], int n, int root)
{
int parent = root;
int child = parent * 2 + 1;//默认左孩子
while (child < n)
{
if (child+1<n && arr[child + 1] > arr[child])//要考虑到有孩子存在不
{
child += 1;
}
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int arr[], int n)
{
//建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, n, i);
}
}2、3 建完堆后进行堆排序
2、3、1 排升序建大堆
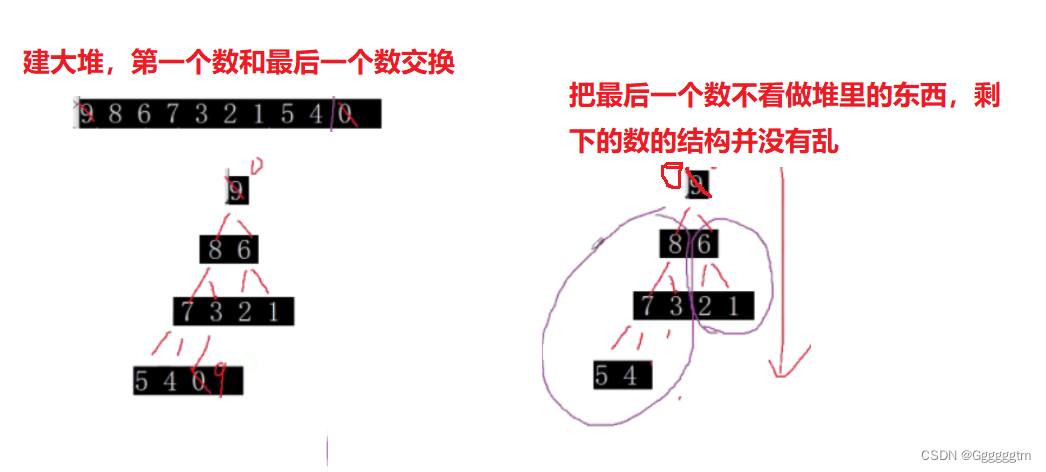
我们知道,大堆的根节点是最大的。同时,根节点总比子节点大。那为什么排升序要建大堆呢?假如是建的小堆,最小数在堆顶,最小的数相当于被选出来了。那么在剩下的始终再去 选数。但是剩下的树结构就乱了,如下图:此时我们需要重新建堆才能选出下一个最小的数。建堆的时间复杂度为O(n),这样的效率就很低了。
我们建大堆,大堆第一个元素是最大的。我们把第一个元素和最后一个元素交换,那么最大的数就到了最后面。然后把最大的数不看做堆里面的数据,此时,剩下的数据的结构并没有乱,如下图:
再对第一个数进行数向下调整,又成为了一个大堆,反复此操作即可排序完成。
2、3、2 建大堆后进行堆排序
由上述我们知道,当我们要排升序时,我们要建的是大堆。当建完大堆后,我们就要进行堆排序。建完堆,交换第一个数据合作后一个数据,再对第一个数据进行向下调整。向下调整完后,有成为一个大堆,再次交换、向下调整。当每个数据都向下调整后,我们的数据就称为了升序。我们看代码的实现:
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustDown(int arr[], int n, int root)
{
int parent = root;
int child = parent * 2 + 1;//默认左孩子
while (child < n)
{
if (child+1<n && arr[child + 1] > arr[child])//要考虑到有孩子存在不
{
child += 1;
}
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int arr[], int n)
{
//建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&arr[0], &arr[end]);
AdjustDown(arr, end, 0);
end--;
}
}
void Print(int arr[], int n)
{
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
}
void TestSort()
{
int arr[10] = { 0,9,8,7,6,5,4,3,2,1 };
int n = 10;
HeapSort(arr, n);
Print(arr, n);
}
int main()
{
TestSort();
return 0;
}以上即为整个堆排序的过程。我们不妨来看几道堆排序的例题。
三、堆排序的例题
2、1 例题1:堆排序
堆排序:
输入一个长度为 n 的整数数列,从小到大输出前 m 小的数。
输入格式:
第一行包含整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
输出格式:
共一行,包含 m 个整数,表示整数数列中前 m 小的数。
数据范围:
1≤m≤n≤10e5 1≤m≤n≤10e5,
1≤数列中元素≤10e9 1≤数列中元素≤10e9输入样例:
5 3 4 5 1 3 2输出样例:
1 2 3这道题我们用堆排序来做一下,我们看答案:
#include<iostream>
#include <algorithm>
using namespace std;
const int N=100010;
int cnt,q[N];
int n,m;
void down(int x)
{
int t=x;
if(x*2+1<cnt&&q[x*2+1]<q[t])
t=x*2+1;
if(x*2+2<cnt&&q[x*2+2]<q[t])
t=x*2+2;
if(t!=x)
{
swap(q[t],q[x]);
down(t);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)
{
scanf("%d",&q[i]);
}
cnt=n;
for(int i=n-1-1>>1;i>=0;i--)
{
down(i);
}
while(m--)
{
printf("%d ",q[0]);
q[0]=q[cnt-1];
cnt--;
down(0);
}
return 0;
}2、2 例题2:模拟堆
维护一个集合,初始时集合为空,支持如下几种操作:
I x,插入一个数 xx;PM,输出当前集合中的最小值;DM,删除当前集合中的最小值(数据保证此时的最小值唯一);D k,删除第 kk 个插入的数;C k x,修改第 kk 个插入的数,将其变为 xx;现在要进行 N 次操作,对于所有第 2 个操作,输出当前集合的最小值。
输入格式:
第一行包含整数 N。
接下来 NN 行,每行包含一个操作指令,操作指令为
I x,PM,DM,D k或C k x中的一种。输出格式:
对于每个输出指令
PM,输出一个结果,表示当前集合中的最小值。每个结果占一行。
数据范围:
1≤N≤10e5 1≤N≤10e5
−10e9≤x≤10e9 −10e9≤x≤10e9
数据保证合法。输入样例:
8 I -10 PM I -10 D 1 C 2 8 I 6 PM DM输出样例:
-10 6我们这道题的所有操作都可以用向下调整,或向上调整都可以玩成。我们看一下答案:
#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
const int N=100010;
int h[N],qh[N],hq[N],cnt;
void heap_swap(int a,int b)
{
swap(qh[hq[a]],qh[hq[b]]);
swap(hq[a],hq[b]);
swap(h[a],h[b]);
}
void down(int u)
{
int t=u;
if(u*2<=cnt&&h[u*2]<h[t])
t=2*u;
if(u*2+1<=cnt&&h[u*2+1]<h[t])
t=2*u+1;
if(t!=u)
{
heap_swap(t,u);
down(t);
}
}
void up(int u)
{
while (u / 2 && h[u] < h[u / 2])
{
heap_swap(u, u / 2);
u >>= 1;
}
}
int main()
{
int n,m=0;
scanf("%d",&n);
while(n--)
{
char op[5];
int k,x;
scanf("%s",op);
if(!strcmp(op,"I"))
{
scanf("%d",&x);
m++;
cnt++;
qh[m]=cnt;
hq[cnt]=m;
h[cnt]=x;
up(cnt);
}
else if(!strcmp(op,"PM"))
{
printf("%d\n",h[1]);
}
else if(!strcmp(op,"DM"))
{
heap_swap(1,cnt);
cnt--;
down(1);
}
else if(!strcmp(op,"D"))
{
scanf("%d",&k);
k=qh[k];
heap_swap(k,cnt);
cnt--;
down(k);
up(k);
}
else
{
scanf("%d%d",&k,&x);
k=qh[k];
h[k]=x;
down(k);
up(k);
}
}
return 0;
}
四、总结
对排序中,重点是要熟知向下调整算法,并且知道排升序建大堆还是小堆。这里给大家总结出各个排序的时间复杂度、空间复杂度、是否稳定性。需要掌握的。
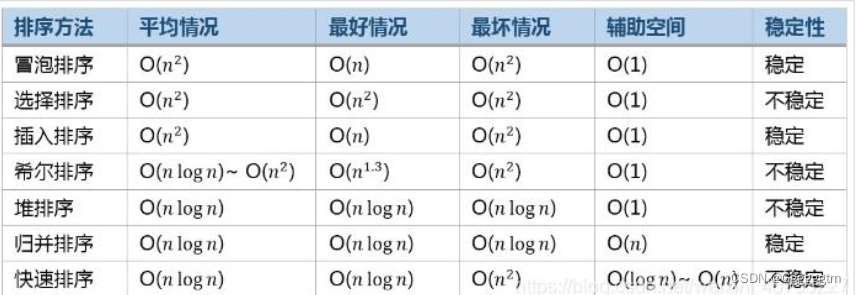
堆排序的讲解就到这里,希望以上内容对你有所帮助。
感谢阅读,ovo~