概率基础——逻辑回归多分类法

news2024/11/24 3:30:37

概率基础——逻辑回归多分类法

逻辑回归是一种经典的分类算法，通常用于解决二分类问题。然而，在实际应用中，我们经常会遇到多分类任务。本文将简单介绍逻辑回归的理论、多分类方法以及优缺点，并提供一个Python实现的示例。

逻辑回归的理论及公式

逻辑回归是一种基于概率的线性分类模型。给定输入特征 $X$ ，逻辑回归通过线性组合加上一个 $s i g m o i d$ 函数（也称为逻辑函数）来计算样本属于正类的概率：

$\frac{1}{1 + e^{-\left(\beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_nX_n\right)}}$

其中， $Y$ 是输出变量（类别）， $X$ 是输入特征， $\beta$ 是模型参数， $e$ 是自然对数的底。

逻辑回归的多分类方法

在逻辑回归中，处理多分类任务通常有两种方法：

1. 修改逻辑回归的损失函数

在传统的二分类逻辑回归中，使用sigmoid函数作为激活函数。但在多分类情况下，我们可以使用softmax函数，将逻辑回归的损失函数修改为交叉熵损失函数。这样可以输出多个类别的预测概率。

2. 将多分类任务分解为多个二分类任务

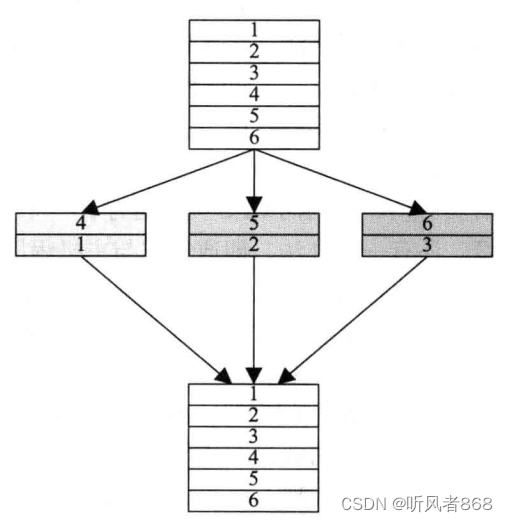
另一种方法是将多分类任务分解为多个二分类任务。常见的分解方法包括：

OvR（One vs Rest）：每次将一个类别样本作为正类，其他类别样本作为负类，生成N个二分类器，最后选取概率最大的类别作为预测结果。
MvM（Many vs Many）：将一部分类别样本作为正类，另一部分类别样本作为负类，生成多个二分类器。通过编码和解码的方式进行分类。
OvO（One vs One）：每次选择两个类别样本进行训练，生成N(N-1)/2个二分类器。在预测时，通过投票法选择最终分类结果。

逻辑回归多分类法的优缺点

优点：

训练速度快，计算量与特征数目相关。
模型简单易于理解，可解释性强。
可以动态调整分类阈值，得到不同的概率预测。

缺点：

特征处理复杂，需要归一化和较多的特征工程。
模型性能有限，只能处理线性可分的数据。
难以处理数据不平衡问题，倾向于将所有样本都预测为占比较大的类别。

Python实现示例

下面通过一个示例，展示了如何使用逻辑回归进行多分类任务的处理。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

# 生成示例数据
X, y = make_classification(n_samples=1000, n_features=20, n_classes=3, n_clusters_per_class=1, random_state=42)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 构建逻辑回归模型
log_reg = LogisticRegression(multi_class='auto', solver='lbfgs')

# 训练模型
log_reg.fit(X_train, y_train)

# 预测测试集
y_pred = log_reg.predict(X_test)

# 绘制y_test和y_pred的图像
plt.figure(figsize=(10, 6))

plt.plot(np.arange(len(y_test)), y_test, 'bo', label='Actual Class')
plt.plot(np.arange(len(y_test)), y_pred, 'r+', label='Predicted Class')
plt.xlabel('Sample Index')
plt.ylabel('Class')
plt.title('Comparison of Actual and Predicted Classes')
plt.legend()
plt.grid(True)
plt.show()

在这里插入图片描述

上述代码中，生成了一些示例数据，并使用逻辑回归模型进行训练和预测。然后，我们将实际的类别（y_test）和预测的类别（y_pred）绘制在同一图像上，以便进行比较。接下来，我们来解释代码的具体内容和绘制结果。

make_classification：用于生成示例数据，创建了一个具有 1000 个样本和 20 个特征的数据集，共有 3 个类别。
train_test_split：用于划分训练集和测试集，测试集占比为 20%。
LogisticRegression：构建逻辑回归模型。
fit：用训练数据拟合模型。
predict：对测试数据进行预测。
绘制图像：使用 matplotlib 库将实际类别和预测类别的值绘制在同一图像上，蓝色点表示实际类别，红色加号表示预测类别。