1. 引言
相信大家已经对普通的01背包或者其他背包问题已经很熟练了,但是有时候我们去解决NP问题(指数级别的复杂度,比如N!),时间复杂度就会非常之大
所以,这个时候我们需要寻找更加优化的方法,来优化DP
状态压缩也是一种DP优化方法
2. 什么是状态压缩?
状态压缩:是一种优化动态规划算法的技术,通常用于解决具有大量状态的问题,以减少内存消耗和提高计算效率。在动态规划问题中,状态通常是指描述问题的各种情况或者组合的变量,而状态压缩就是通过一种巧妙的方式来表示和存储状态,从而减少内存消耗。
也就是说,当DP状态是集合的时候,把集合的组合或者排列用二进制进行表示,这个二进制01组合表示集合的的一个子集 , 可以将DP状态的处理转成为二进制的位操作,能够提高算法的效率
当一个DP具有以下特征的时候,就适合用状态压缩了:
- 状态之间存在某种转移关系,但状态数量巨大。
- 状态之间的转移可以通过位运算来表示。
- 状态之间的转移关系可以通过枚举子集或者排列组合的方式来计算。
3. 引子
现在,我们来看一道经典问题,一起学习什么是状态压缩。
给定一张 n个点的带权无向图,点从 0∼n−1标号,求起点 0到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0到 n−1不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。接下来 n行每行 n个整数,其中第 i行第 j个整数表示点 i到 j的距离(记为 a[i,j])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。数据范围
1≤n≤200≤a[i,j]≤107
输入样例:
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例:
1
Hamilton(旅行商)是一个NP问题,N个点的全排列,时间复杂度是n!这是非常之大的。
有人看到最短路或许会无脑dijkstra, 但是对于dijkstra求最短路是并没有考虑每个点的
这道题的难度就在每个点都需要访问一次,所以并不能适用
就算使用回溯搜索,那也非常大的时间复杂度
4. DP求解Hamilton问题
4.1 状态定义
如何进行DP状态定义,这是我们首要解决的
DP问题,无非就是从小问题递推到大问题,那么我们可以这样进行dp定义:
:代表在S集合内,到达j点的最短距离(j也在S集合内,因为每个点都需要到达)
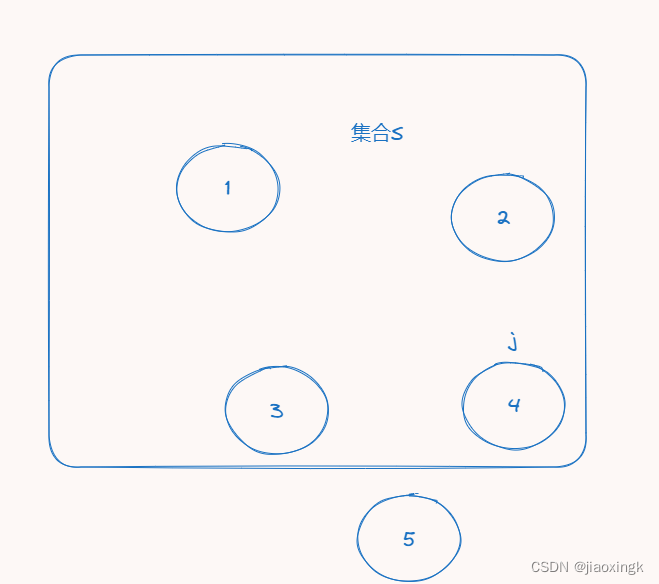
我们可以通过子集然后递推求出大集合
4.2 属性定义
这道题很明确,其实就是求最小值,也就是
4.3 状态转移
从集合S到j点的最短距离,无非就是需要从前面的集合开始入手
我们可以从小问题递推到大问题
:代表从集合S中去除
点的集合
如何从递推到
又是一个难题,我们可以设k为
中的一个点,把0~j 分为两个部分:
第一部分就是:0->k , 第二部分是k->j
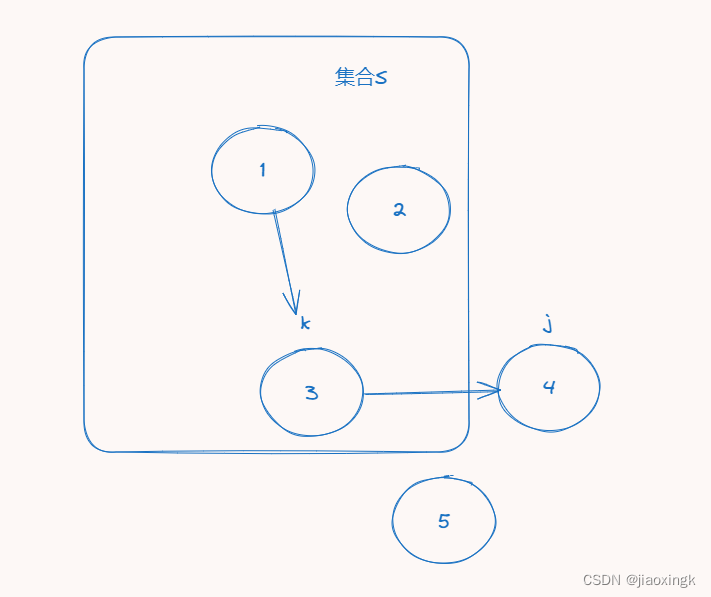
我们先到k点,然后从k点到j点,于是就有了以下状态转移方程式:
:k到j的距离
这个地方会比较难以理解,但是要清楚:DP就是从小问题递推到大问题
我们要求S集合内到达j点的最短路,无非就是要从S中把j点去除,然后通过中间的那些点作为媒介,一个一个递推到S -> j
5. 代码
知道这些,我们可以开始编码了:
解析:
- 状态压缩,是将一个二进制数表示一个集合S,二进制的每一位都代表图上的每一个点。
- 对于二进制位每一位来说,有1就代表全都有,比如n = 5时,二进制为:11111 , 也就代表这个集合里面有1、2、3、4、5几个点
from math import *
n = int(input())
dist = [[0] * (n + 1) for i in range(n + 1)] # 两个点之间的距离
for i in range(n):
a = list(map(int, input().split()))
for j in range(len(a)):
dist[i][j] = a[j]
# 集合S到j的最短距离 , 这里的1 << 20是因为题目的范围是1 - 20 , 最大只有20个点,通过位运算的形式,将这21个点转为集合
dp = [[inf] * (n + 1) for i in range(1 << 20)] # 初始化都是最大的
dp[1][0] = 0 # 最开始,集合里面只有一个0点
for s in range(1 << n): # 二进制总共的位数
for j in range(n):
if (s >> j) & 1: # 判断j是否在S中
for k in range(n):
if (s ^ (1 << j)) >> k & 1: # 判断k是否在S除去j里面
dp[s][j] = min(dp[s][j], dp[s ^ (1 << j)][k] + dist[k][j]) # 状态转移方程
print(dp[(1 << n) - 1][n - 1])