---

前言

直接选择排序是一种简单的排序算法。它的工作原理是每一次从未排序部分选出最小（或最大）的一个元素，存放到排序序列的起始位置，然后再从剩余未排序元素中继续寻找最小（或最大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。这种算法的时间复杂度为O(n^2)，其中n是待排序元素的数量，因此在处理大数据集时效率较低。然而，它的实现简单，对于小规模的数据排序是一个不错的选择。

---

一、选择排序的基本思想：

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完 。

选择排序的基本思想是从未排序的序列中找到最小（或最大）的元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（或最大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

这种排序算法的优点在于其实现过程相对简单，对于小规模的数据排序，其效率是可以接受的。然而，选择排序也存在明显的缺点。由于其每次都需要从未排序的元素中找到最小（或最大）的元素，这导致算法的时间复杂度为O(n^2)，其中n为待排序元素的数量。这意味着当处理大规模数据时，选择排序的性能可能会变得非常低下。

在实际应用中，选择排序往往不是最优的选择，特别是对于大规模数据的排序。更高效的排序算法，如快速排序、归并排序、堆排序等，在处理大规模数据时，通常会有更好的性能表现。

但是，选择排序的思想在某些特定情境下仍然有其应用价值。例如，在某些需要稳定排序且数据量较小的场景中，选择排序可以作为一个简单且有效的解决方案。此外，选择排序的思想也可以作为其他更复杂排序算法的基础，帮助理解和学习更高级的排序算法。

总的来说，选择排序的基本思想虽然简单，但其性能上的局限性使得它在实际应用中并不常见。然而，这并不意味着它没有价值，通过深入理解和应用选择排序的思想，我们可以更好地理解排序算法的本质，并为学习更高级的排序算法打下坚实的基础。

二、直接选择排序

• 在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
• 若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换
• 在剩余的array[i]--array[n-2]（array[i+1]--array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素

直接选择排序是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

首先，我们假设有一个无序的整数列表，我们想要通过直接选择排序将其按升序排列。算法的工作流程可以分为以下几个步骤：

1. 找到最小（大）元素：在列表中找到最小（大）的元素。这个步骤通常涉及遍历整个列表，比较每个元素的值。
2. 交换位置：一旦找到最小（大）元素，将其与列表的第一个元素交换位置。这样，最小（大）的元素就被放到了它应该在的位置。
3. 移除已排序元素：从列表中移除已排序的第一个元素（现在是最小（大）元素），然后对剩余的元素重复上述两个步骤。
4. 重复过程：继续这个过程，每次从剩余的未排序元素中找到最小（大）元素，并将其与未排序部分的第一个元素交换。
5. 结束条件：当整个列表都被排序时，算法结束。

直接选择排序的时间复杂度是O(n^2)，其中n是列表的长度。这是因为它包含两个嵌套循环：一个用于找到最小（大）元素，另一个用于遍历整个列表。尽管这种排序方法在处理小型或中型列表时可能是有效的，但对于大型列表，更高效的排序算法（如快速排序、归并排序或堆排序）通常是更好的选择。

然而，直接选择排序有一个显著的优点，那就是它的实现相对简单，对于初学者来说是一个很好的学习工具。通过理解这个算法，可以对排序的基本概念有一个直观的认识，从而为学习更复杂的排序算法打下基础。

在实际应用中，直接选择排序可能不是最优选择，但它在教育、演示和教学方面仍然具有很高的价值。此外，对于某些特定类型的数据集（如部分有序的数据集），直接选择排序的性能可能会比其他算法更好。

三、直接选择排序的特性总结：

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

直接选择排序的特性总结起来，主要是其直观易懂、原地排序和不稳定排序的特点。

直接选择排序是一种简单直观的排序算法，其基本原理是每一次从未排序的部分选出最小（或最大）的一个元素，存放到排序序列的起始位置。它的操作过程是从左到右逐个选择剩余元素中的最小者，并将其与未排序部分的第一个元素交换。这种选择过程一直持续到未排序部分为空，排序也就完成了。因此，直接选择排序的直观性是其显著特点之一，使得初学者容易理解和实现。

另一个特性是原地排序，这意味着直接选择排序不需要额外的存储空间来进行排序，它直接在原始数组上进行操作，改变了原始数组的顺序。这一特性使得它在处理内存受限的场景时非常有用。

然而，直接选择排序也是一种不稳定的排序算法。稳定性是指如果两个元素的键值相等，那么在排序之后它们的相对位置不会改变。由于直接选择排序在每次选择最小（或最大）元素进行交换时，可能会改变相等元素的原始相对位置，因此它不具备稳定性。

总的来说，直接选择排序是一种简单直观、原地进行的排序算法，但它是不稳定的。在实际应用中，根据数据的特性和排序要求，可能需要选择更合适的排序算法。例如，对于大规模数据集，直接选择排序的效率可能较低，因为它需要多次遍历和交换操作。而对于小规模数据集或者对稳定性要求不高的场景，直接选择排序则是一个简单有效的选择。

四、直接选择排序的动画展示

直接选择排序是一种简单的排序算法。它通过每次从未排序部分选择最小（或最大）元素，与未排序部分的第一个元素交换位置，从而达到排序的目的。在动画展示中，可以看到每次选择的最小（或最大）元素逐步“冒泡”到已排序部分的末尾，直到整个序列有序。这种排序方法的时间复杂度为O(n^2)，适用于小规模数据的排序。

五、直接选择排序的代码展示

test.c

#include<stdio.h>
#include<stdlib.h>
#include<time.h>

void SelectSort(int* a, int n);
void PrintArray(int* a, int n);
void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void TestSelectSort()
{
	int a[] = { 5, 13, 9, 16, 12, 4, 7, 1, 28, 25, 3, 9, 6, 2, 4, 7, 1, 8 };
	//int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };
	PrintArray(a, sizeof(a) / sizeof(int));

	SelectSort(a, sizeof(a) / sizeof(int));

	PrintArray(a, sizeof(a) / sizeof(int));
}


void PrintArray(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}
void TestOP()
{
	srand(time(0));
	const int N = 10000;
	int* a1 = (int*)malloc(sizeof(int) * N);

	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
	}


	int begin1 = clock();
	SelectSort(a1, N);
	int end1 = clock();

	
	
	printf("SelectSort:%d\n", end1 - begin1);

	free(a1);
}
void SelectSort(int* a, int n)
{
	for (int k = 0; k < n; k++)
	{
		int max = 0;
		for (int i = 0; i < n - k; i++)
		{
			if (a[i] >= a[max])max = i;
		}
		Swap(&a[n - 1 - k], &a[max]);
	}
	
}
int main()
{
	TestSelectSort();
	TestOP();

	return 0;
}

这段代码实现的是选择排序（Selection Sort）算法，而不是通常的冒泡排序（Bubble Sort）。选择排序是一种简单直观的排序算法，它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

接下来我将逐步解释这段代码：

1. 函数定义：

void SelectSort(int* a, int n)

这是一个名为 SelectSort 的函数，它接受一个整数数组 a 和一个整数 n 作为参数。n 是数组 a 的长度。

2. 外层循环：for (int k = 0; k < n; k++)

这个循环从 0 到 n-1 迭代，用于确定当前应该放置最小元素的位置。

3. 初始化 max 变量：int max = 0;

在每次外层循环开始时，max 被初始化为 0。这个变量用于存储当前找到的最小元素的位置。

4. 内层循环：for (int i = 0; i < n - k; i++)

这个循环从 0 到 n-k-1 迭代。每次迭代，它都会检查从 a[0] 到 a[n-k-1] 的元素，以找到当前最小元素的位置。

5. 判断并更新最小元素的位置：if (a[i] >= a[max]) max = i;

这个条件检查 a[i] 是否大于或等于 a[max]。如果是，则更新 max 为 i。注意这里使用了 >= 而不是 >，这意味着如果有多个相同的最小元素，它们都会被正确地处理。

6. 交换元素：Swap(&a[n - 1 - k], &a[max]);

在内层循环结束后，我们已经找到了从 a[0] 到 a[n-k-1] 中的最小元素，它的位置是 max。现在，我们需要将这个最小元素与当前位置 n-1-k 的元素交换。

整体上，这段代码通过不断地选择并交换最小元素，最终将数组 a 排序为升序。

六、直接选择排序的优化

使用min和max对直接选择排序进行优化可以减少交换的次数。

在原始的直接选择排序算法中，每次迭代会通过查找最小值和最大值的索引来确定需要交换的元素。然后分别进行交换。这样可能会导致不必要的交换操作。

优化的思路是，在每次迭代中，同时查找最小值和最大值的索引，然后将它们记录下来，最后再进行一次交换操作。

具体实现如下：

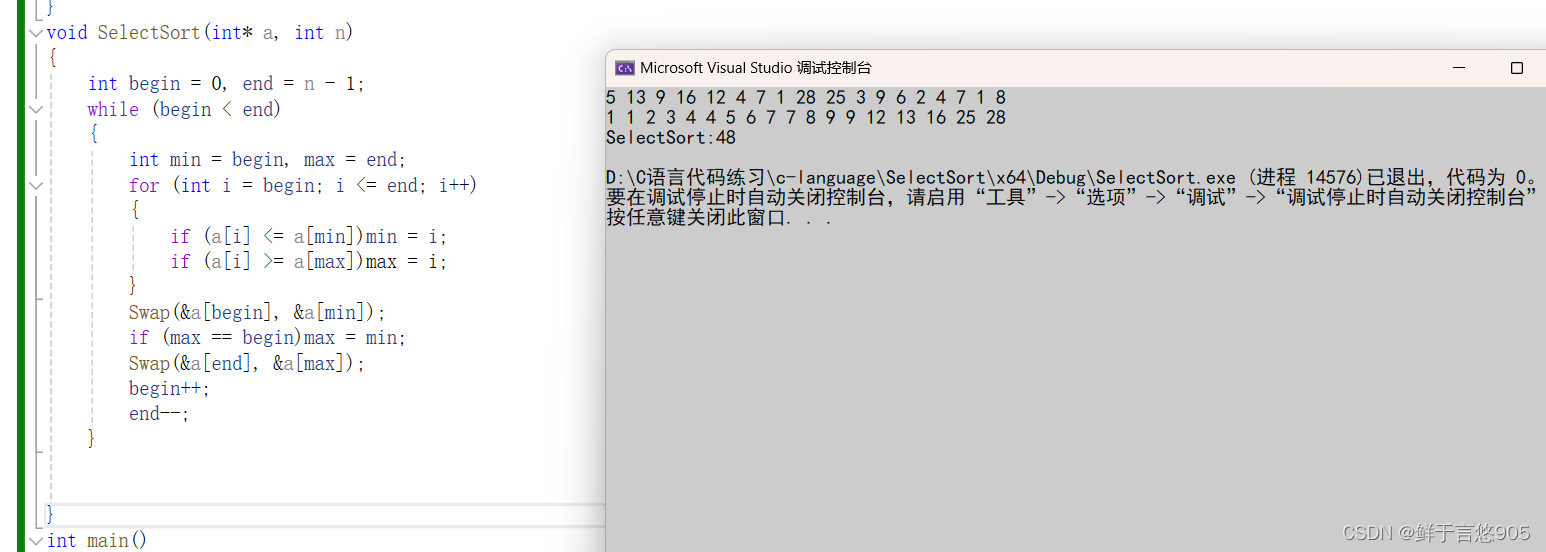
void SelectSort(int* a, int n)
{
    int begin = 0, end = n - 1;
    while (begin < end)
    {
        int min = begin, max = end;
        for (int i = begin; i <= end; i++)
        {
            if (a[i] <= a[min]) min = i;
            if (a[i] >= a[max]) max = i;
        }

        // 将最小值放到已排序部分的起始位置
        Swap(&a[begin], &a[min]);
        
        // 如果最大值的索引是begin，将最大值的索引更新为min
        if (max == begin) max = min;
        
        // 将最大值放到已排序部分的末尾位置
        Swap(&a[end], &a[max]);
        
        begin++;
        end--;
    }
}

这样的优化可以减少交换的次数，提高排序的效率。同时，可以确保每次迭代只进行一次交换操作，减少了内存的读写次数，提高了算法的性能。

 if (max == begin) max = min;

关于这个代码是为了防止min正好在end,而max正好在begin这种的特殊情况

test.c

#include<stdio.h>
#include<stdlib.h>
#include<time.h>

void SelectSort(int* a, int n);
void PrintArray(int* a, int n);
void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void TestSelectSort()
{
	int a[] = { 5, 13, 9, 16, 12, 4, 7, 1, 28, 25, 3, 9, 6, 2, 4, 7, 1, 8 };
	//int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };
	PrintArray(a, sizeof(a) / sizeof(int));

	SelectSort(a, sizeof(a) / sizeof(int));

	PrintArray(a, sizeof(a) / sizeof(int));
}


void PrintArray(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}
void TestOP()
{
	srand(time(0));
	const int N = 10000;
	int* a1 = (int*)malloc(sizeof(int) * N);

	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
	}


	int begin1 = clock();
	SelectSort(a1, N);
	int end1 = clock();

	
	
	printf("SelectSort:%d\n", end1 - begin1);

	free(a1);
}
void SelectSort(int* a, int n)
{
	int begin = 0, end = n - 1;
	while (begin < end)
	{
		int min = begin, max = end;
		for (int i = begin; i <= end; i++)
		{
			if (a[i] <= a[min])min = i;
			if (a[i] >= a[max])max = i;
		}
		Swap(&a[begin], &a[min]);
		if (max == begin)max = min;
		Swap(&a[end], &a[max]);
		begin++;
		end--;
	}
	
	
}
int main()
{
	TestSelectSort();
	TestOP();

	return 0;
}

这段代码实现的是选择排序算法，用于对数组a中的元素进行排序。传入参数是数组a和数组长度n。

代码的主要思路是：通过每一次迭代，从未排序的元素中找到最小值和最大值，并将它们分别放到已排序部分的起始位置和末尾位置。然后缩小未排序部分的范围，再次进行迭代直至完成排序。

1. 初始化变量begin为数组的起始索引0，end为数组的终止索引n-1。
2. 进入循环，判断begin是否小于end。如果是，继续下面的操作；如果不是，说明排序已完成，退出循环。
3. 在每一次迭代中，定义变量min和max，分别用于记录当前未排序部分的最小值和最大值的索引，初始值分别设为begin和end。
4. 从begin到end遍历数组a，找到当前最小值和最大值的索引，更新min和max。
5. 交换最小值和begin位置的元素，使当前最小值放到已排序部分的起始位置。
6. 如果max等于begin，说明最大值原本就在begin位置，交换后已经移到了最小值应该在的位置，所以需要将max更新为min。
7. 交换最大值和end位置的元素，使当前最大值放到已排序部分的末尾位置。
8. 完成一次迭代后，已排序部分的范围向两端缩小，begin增加1，end减少1。
9. 重复2-8步骤，直到begin不小于end，排序完成。

总结起来，选择排序每次迭代都会确定未排序部分的最小值和最大值的位置，并将它们交换到已排序部分的起始和末尾位置。通过多次迭代，最终达到整个数组的有序状态。

---