opencv 傅里叶变换（低通滤波 + 高通滤波）

文章目录

1、傅里叶变换
2、通过numpy实现
3、高通滤波器
5、通过opencv实现傅里叶变换
6、低通滤波器
7、C++实现傅里叶变换

1、傅里叶变换

时域分析：以时间作为参照物，世间万物都是随着时间变化而变化，并且不会停止
频域分析：认为世间万物都是静止的，永恒不变的

通过以下制作饮料的过程可以很好的理解傅里叶变换。

1、从时域分析：就是六点零一放了1块冰糖，3颗红豆，2颗绿豆，4块西红柿，1杯纯净水，六点零二放了1块冰糖。。。。随着时间的变化一直在变化

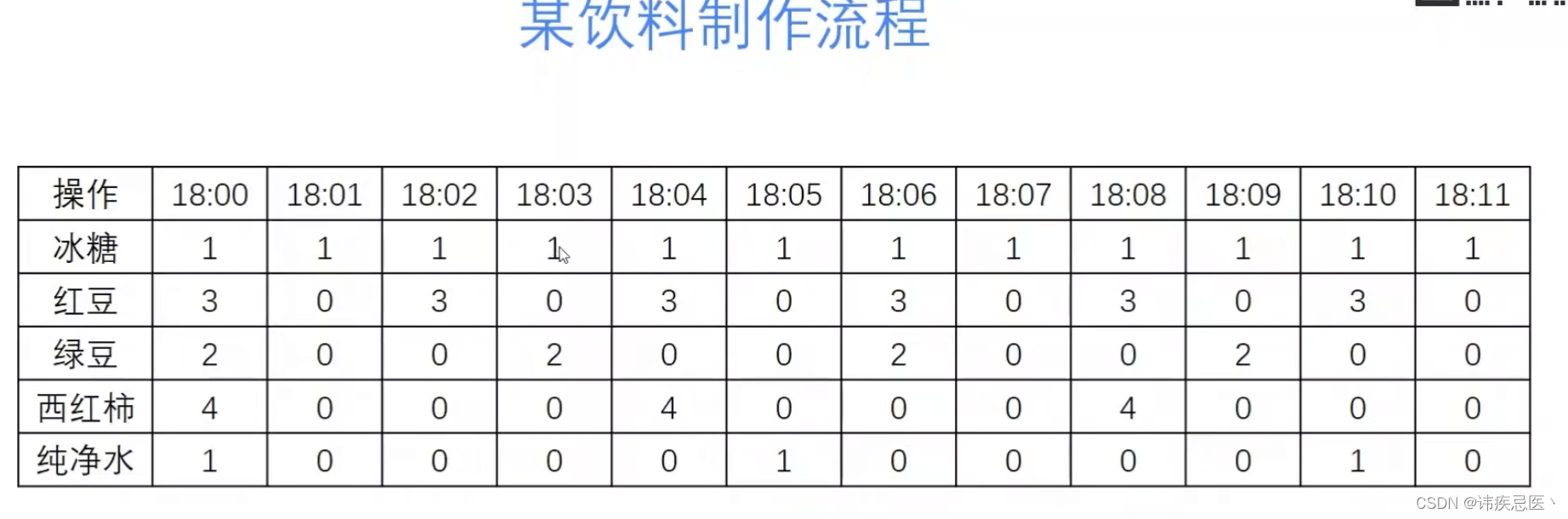
在这里插入图片描述
2、从频域角度分析：不在是以时间为参照物了，而是这个事情的频率，1分钟放1块冰糖，2分钟放3粒红豆，3分钟放2粒绿豆，4分钟放4块西红柿，5分钟放1杯水。

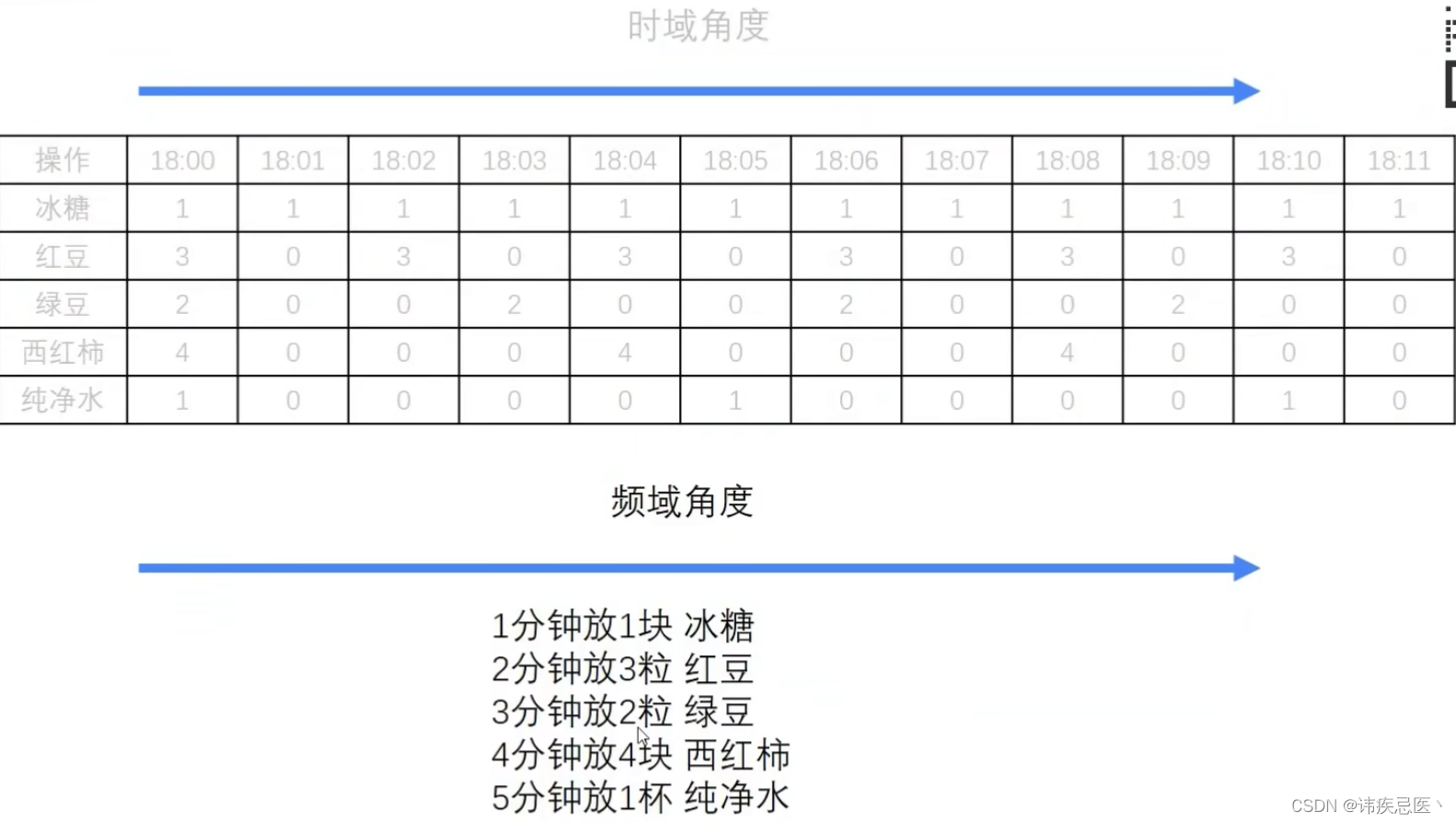
下面这两个图都是描述同一个事情，可以更明显看出，两者的区别。
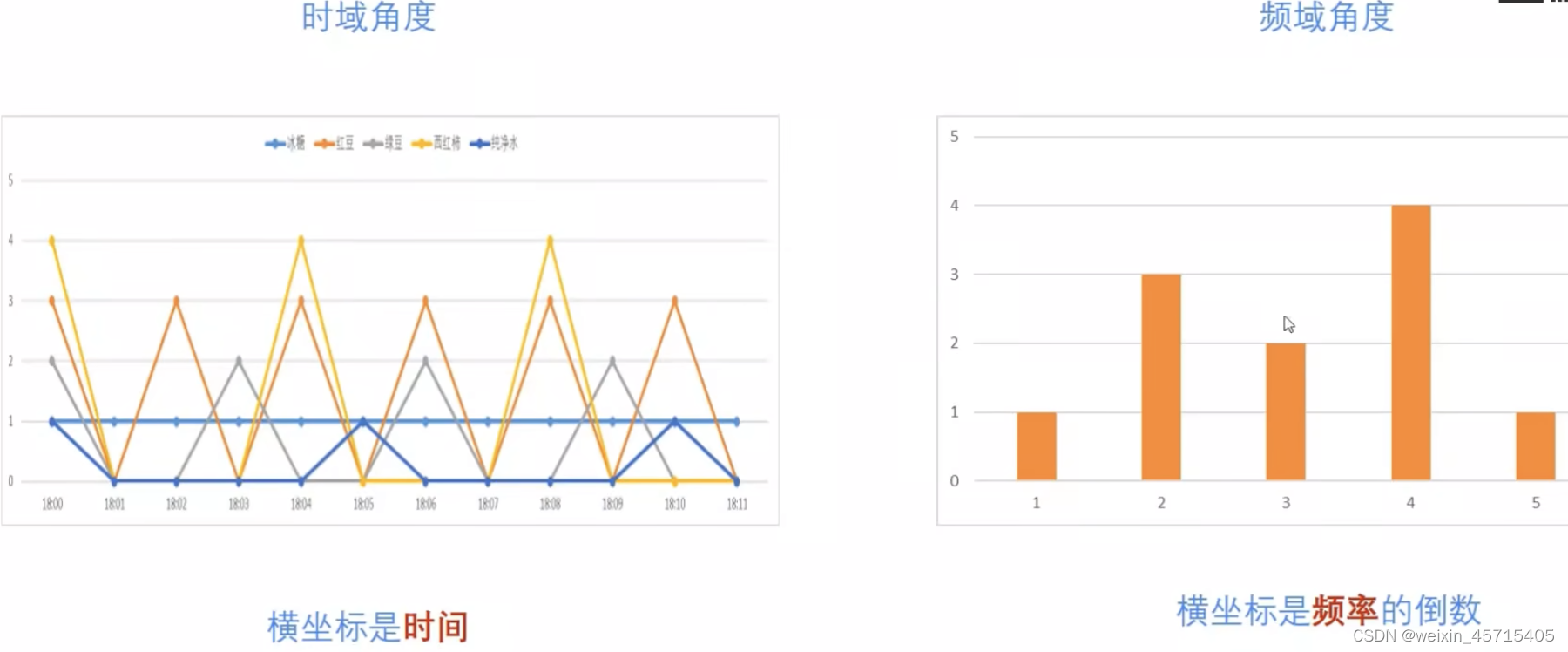
在这里插入图片描述
在两个角度去看周期函数的变化

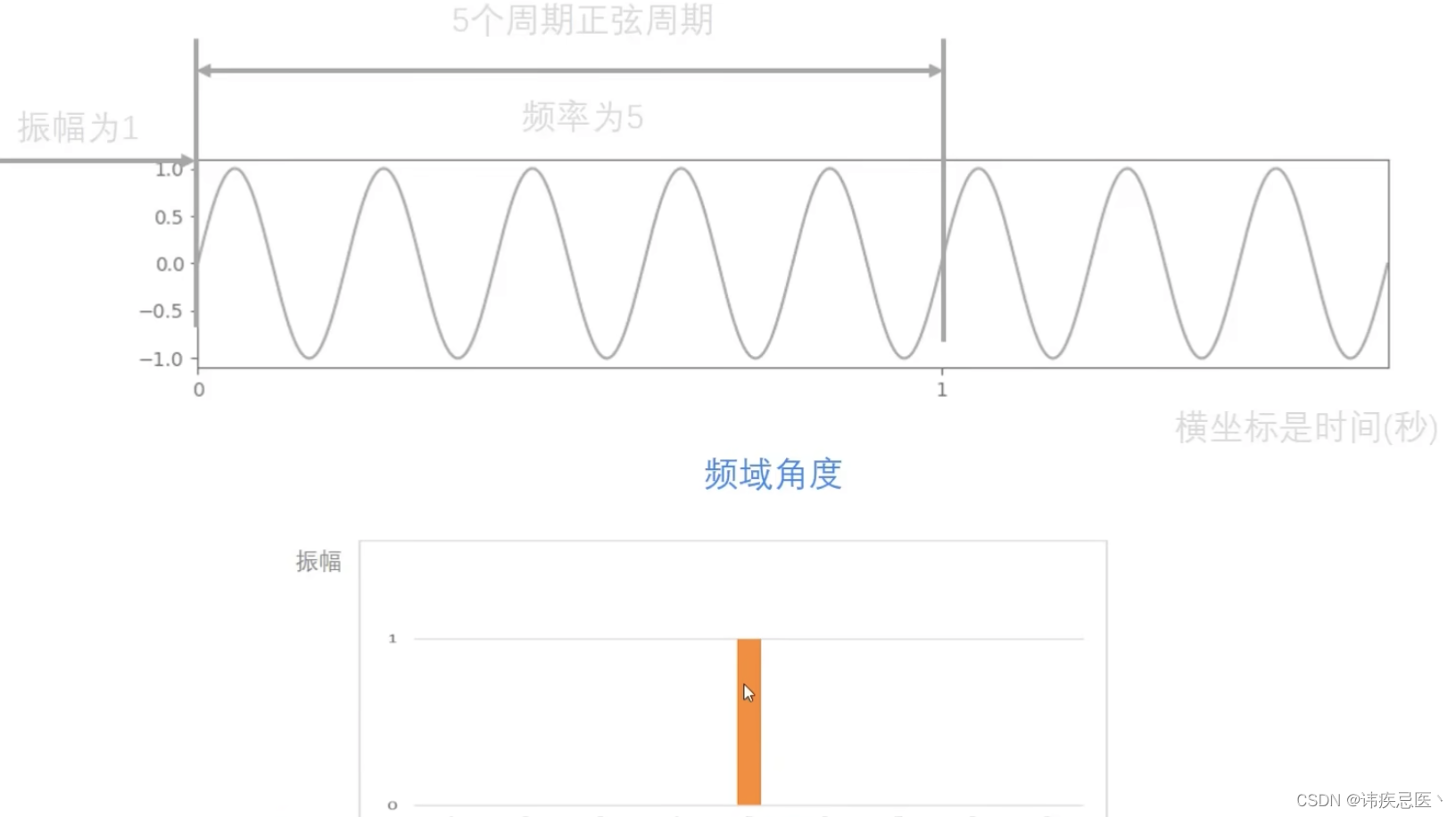
任何连续的周期信号，可以由一组适当的正𫠊曲线组成

相为：三个开始起点不一致的余𫠊函数，组成了这个曲线
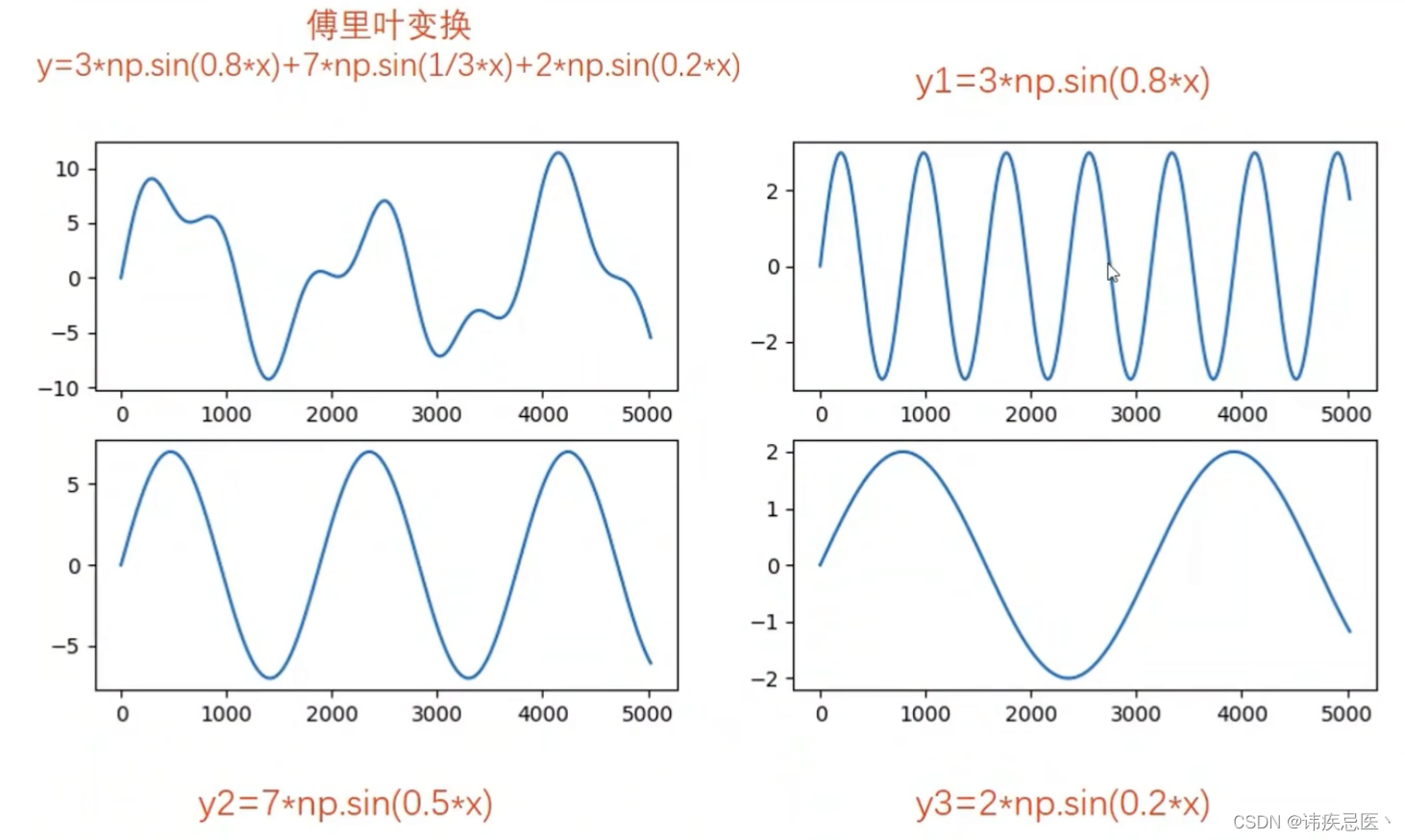
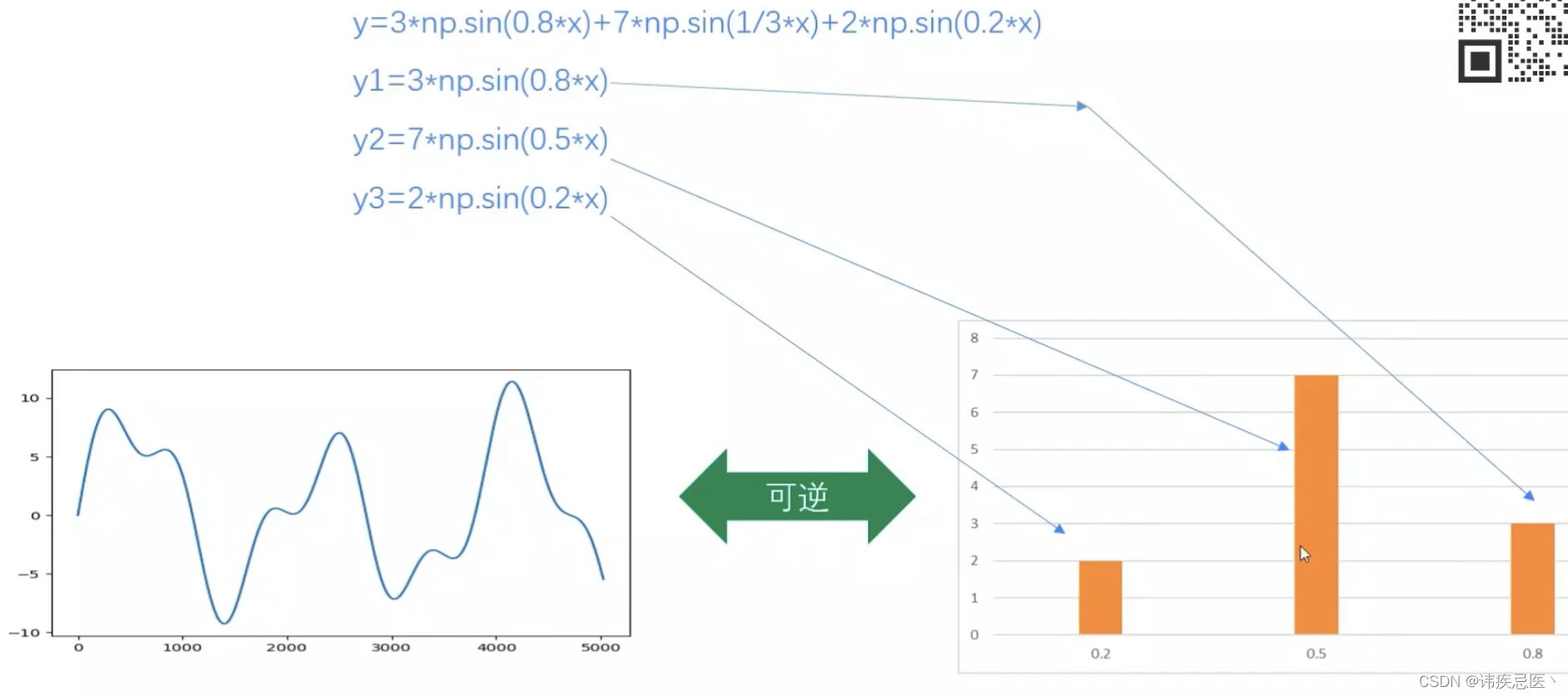
在这里插入图片描述

2、通过numpy实现

通过将原图进行傅里叶变换，得到频域图像，获得高频和低频，对高频和低频进行操作之后，进行逆变换回原图像达到对图像进行特色操作：图像增强、图像去噪、边缘检测、特征提取、压缩、加密等
1、低通滤波器：只保留低频信息，去掉高频信息，会去掉边缘特征信息，会让图像变模糊
2、高频滤波器：只保留高频信息，去掉低频信息，会增强图像的边缘和特征信息，但是会失去一些细节信息

def test9():
    img = cv2.imread("1.jpg", 0)
    # 执行傅里叶变换，转化为频域
    f = np.fft.fft2(img)
    # 低频在左上角，为了方便，将其移到中心位置（带负数的数组）
    fshift = np.fft.fftshift(f)
    # 通过将其转换为（0-255）中
    result = 20 * np.log(np.abs(fshift))

    # 原图显示
    # 创建窗口一行两列，第一咧
    plt.subplot(121)
    plt.imshow(img, cmap='gray')
    plt.title('orginal')
    # 不用坐标系
    plt.axis('off')

    # 傅里叶变换之后的图
    plt.subplot(122)
    plt.imshow(result, cmap='gray')
    plt.title('result')
    plt.axis('off')
    plt.show()

在这里插入图片描述

从频域转换会原图像（因为没有做任何操作，所以输出图像不会发生改变）

def test10():
    img = cv2.imread("1.jpg", 0)
    # 执行傅里叶变换，转化为频域
    f = np.fft.fft2(img)
    # 低频在左上角，为了方便，将其移到中心位置（带负数的数组）
    fshift = np.fft.fftshift(f)

    # 低频谱从中心移动到左上角（相当于又移回去）
    ishift = np.fft.ifftshift(fshift)
    # 从频域转换回原图像
    iimg = np.fft.ifft2(ishift)
    iimg = np.abs(iimg)

    # 原图显示
    # 创建窗口一行两列，第一咧
    plt.subplot(121)
    plt.imshow(img, cmap='gray')
    plt.title('orginal')
    # 不用坐标系
    plt.axis('off')

    # 傅里叶变换之后的图
    plt.subplot(122)
    plt.imshow(iimg, cmap='gray')
    plt.title('result')
    plt.axis('off')
    plt.show()

在这里插入图片描述

3、高通滤波器

前面已经说过，高通滤波器是去除所有低频信息，达到图像增强的效果但是会失去一些细节信息。

def test11():
    img = cv2.imread("1.jpg", 0)
    # 执行傅里叶变换，转化为频域
    f = np.fft.fft2(img)
    # 低频在左上角，为了方便，将其移到中心位置（带负数的数组）
    fshift = np.fft.fftshift(f)

    # 高宽 创建高通滤波器
    rows, cols = img.shape
    crows, ccols = int(rows / 2), int(cols / 2)
    # 前面我们将低频信息移动到图像中间来了
    # 这里将低频信息全部设置为0，达到去掉低频信息目的
    fshift[crows - 30:crows + 30, ccols - 30:ccols + 30] = 0

    ifshift = np.fft.ifftshift(fshift)
    # 将频谱逆变换到图像
    iimg = np.fft.ifft2(ifshift)
    iimg = np.abs(iimg)

    plt.subplot(121)
    plt.imshow(img, cmap='gray')
    plt.title('orginal')
    # 不用坐标系
    plt.axis('off')

    # 傅里叶变换之后的图
    plt.subplot(122)
    plt.imshow(iimg, cmap='gray')
    plt.title('result')
    plt.axis('off')
    plt.show()

在这里插入图片描述

5、通过opencv实现傅里叶变换

使用opencv中的函数实现

def test12():
    img = cv2.imread("1.jpg", 0)

    # dft返回的是两个通道的频域，0是频域实部分，1是频域图像虚部分
    # DFT_COMPLEX_OUTPUT输出复数
    dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
    dftshift = np.fft.fftshift(dft)

    idftshift = np.fft.ifftshift(dftshift)
    # 傅里叶逆变换
    iimg = cv2.idft(idftshift)
    # magnitude函数频域图像的幅度谱
    # result = 20 * np.log(cv2.magnitude(dftshift[:, :, 0], dftshift[:, :, 1]))

    result = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1])

    plt.subplot(121)
    plt.imshow(img, cmap='gray')
    plt.title('orginal')
    # 不用坐标系
    plt.axis('off')

    # 傅里叶变换之后的图
    plt.subplot(122)
    plt.imshow(result, cmap='gray')
    plt.title('result')
    plt.axis('off')
    plt.show()

在这里插入图片描述

6、低通滤波器

创建一个mask，将中心位置设为1，其他位置设为0，然后和频谱图像相乘之后就只保留了低频信息了

在这里插入图片描述

def test13():
    img = cv2.imread("1.jpg", 0)

    # # 执行傅里叶变换
    dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
    ifshift = np.fft.fftshift(dft)

    # 创建低通滤波器
    rows, cols = img.shape
    mask = np.zeros((rows, cols, 2), np.int8)
    crows, ccols = int(rows / 2), int(cols / 2)
    mask[crows - 30:crows + 30, ccols - 30:ccols + 30] = 1
    fshift = ifshift * mask

    ishift = np.fft.ifftshift(fshift)
    io = cv2.idft(ishift)

    result = cv2.magnitude(io[:, :, 0], io[:, :, 1])

    plt.subplot(121)
    plt.imshow(img, cmap='gray')
    plt.title('orginal')
    # 不用坐标系
    plt.axis('off')

    # 傅里叶变换之后的图
    plt.subplot(122)
    plt.imshow(result, cmap='gray')
    plt.title('result')
    plt.axis('off')
    plt.show()

在这里插入图片描述

7、C++实现傅里叶变换

傅里叶变换：cv::dft()
执行一维或二维浮点数组的正向或反向离散傅里叶变换。

#include <opencv2/core.hpp>
函数说明：void cv::dft( InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0 );
输入参数：
				（1）src					输入数组。可以是实数也可以是复数。
				（2）dst					输出数组。其大小和类型取决于flags。
				（3）flags = 0				转换标志。
									cv::DFT_INVERSE 				执行1D或2D逆变换，而不是默认的正转换。
									cv::DFT_SCALE 					缩放比例标识符，输出的结果会以1/N进行缩放。N=数组元素的数量
									cv::DFT_ROWS 					对输入矩阵的每一行执行正变换或逆变换。能够同时处理多个向量，并减少3D和高维变换的开销。
									cv::DFT_COMPLEX_OUTPUT 			一维或二维实数数组正变换。
									cv::DFT_REAL_OUTPUT 			一维或二维复数数组逆变换。
									cv::DFT_COMPLEX_INPUT 			指定输入为实数输入。输入必须有2个通道。
									cv::DCT_INVERSE					执行逆1D或2D转换，而不是默认的正向转换。
									cv::DCT_ROWS 					对输入矩阵的每一行执行正变换或逆变换。能够同时处理多个向量，并减少3D和高维变换的开销。
				（4）nonzeroRows = 0		默认值为0。若设为非零值，dft函数会将该值作为非零行的有效区间长度，只对非零行进行处理，提高计算效率。

傅里叶反变换：cv::idft()
计算一维或二维阵列的离散傅里叶反变换。
默认情况下，dft和idft都不会缩放结果。因此，您应该显式地将DFT_SCALE传递给dft或idft中的一个，以使这些变换相互逆。

#include <opencv2/core.hpp>
函数说明：void cv::idft( InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0 );
输入参数：
				（1）src					输入数组。可以是实数也可以是复数。
				（2）dst					输出数组。其大小和类型取决于flags。
				（3）flags = 0				转换标志。
									cv::DFT_INVERSE 				执行1D或2D逆变换，而不是默认的正转换。
									cv::DFT_SCALE 					缩放比例标识符，输出的结果会以1/N进行缩放。N=数组元素的数量
									cv::DFT_ROWS 					对输入矩阵的每一行执行正变换或逆变换。能够同时处理多个向量，并减少3D和高维变换的开销。
									cv::DFT_COMPLEX_OUTPUT 			一维或二维实数数组正变换。
									cv::DFT_REAL_OUTPUT 			一维或二维复数数组逆变换。
									cv::DFT_COMPLEX_INPUT 			指定输入为实数输入。输入必须有2个通道。
									cv::DCT_INVERSE					执行逆1D或2D转换，而不是默认的正向转换。
									cv::DCT_ROWS 					对输入矩阵的每一行执行正变换或逆变换。能够同时处理多个向量，并减少3D和高维变换的开销。
				（4）nonzeroRows = 0		默认值为0。若设为非零值，dft函数会将该值作为非零行的有效区间长度，只对非零行进行处理，提高计算效率。

计算相位谱：cv::phase()
计算由x和y的对应元素组成的每个2D矢量的旋转角度。计算公式：angle(I)=atan2(y(I), x(I))
角度估计精度约为0.3度。当x(I)=y(I)=0时，对应角(I)设为0

#include <opencv2/core.hpp>
函数说明：void cv::phase( InputArray x, InputArray y, OutputArray angle, bool angleInDegrees = false );
输入参数：
				（1）x					输入二维矢量的x坐标的浮点数组。
				（2）y					输入二维矢量的y坐标数组。它必须和x有相同的大小和类型。
				（3）angle				角度。输出与x大小和类型相同的数组。
				（4）angleInDegrees = false		当为true时，该函数以度数计算角度，否则以弧度计算。

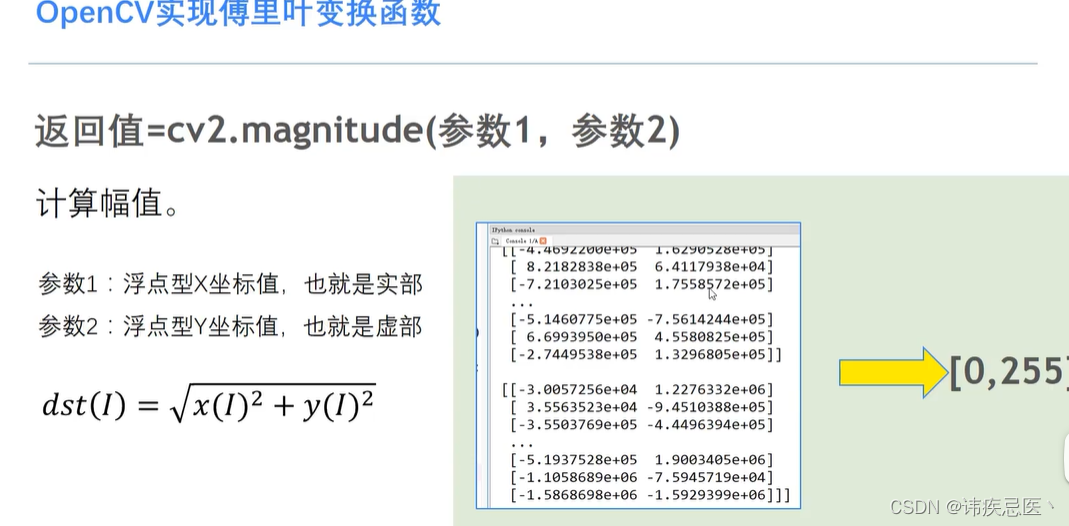
计算幅度谱：cv::magnitude()
计算由x和y数组的相应元素组成的2D向量的大小。计算公式：dst(I) = sqrt(x(I)^2 + y(I)^2)

#include <opencv2/core.hpp>
函数说明：void cv::magnitude( InputArray x, InputArray y, OutputArray magnitude );
输入参数：
				（1）x					输入二维矢量的x坐标的浮点数组。
				（2）y					输入二维矢量的y坐标数组。它必须和x有相同的大小和类型。
				（3）magnitude 			幅值。输出与x大小和类型相同的数组。

计算x和y的坐标：cv::polarToCart()
通过二维矢量的大小和角度来计算x和y的坐标。估计坐标的相对精度约为1e-6。
计算公式：x(I) = magnitude(I) * cos(angle(I))
计算公式：y(I) = magnitude(I) * sin(angle(I))

#include <opencv2/core.hpp>
函数说明：void cv::polarToCart( InputArray magnitude, InputArray angle, OutputArray x, OutputArray y, bool angleInDegrees = false );
输入参数：
				（1）magnitude			输入二维矢量（大小）的浮点数组。若为空矩阵，则假设所有的大小都是=1;若不为空，则必须具有与angle相同的大小和类型。
				（2）angle				输入二维矢量（角度）的浮点数组。
				（3）x					二维矢量的x坐标输出数组。它有相同的尺寸和类型的角度。
				（4）y					二维矢量的y坐标输出数组。它有相同的尺寸和类型的角度。
				（5）angleInDegrees = false  	当为true时，输入角以度数表示，否则以弧度表示。

获取最适合傅里叶正变换的宽 / 高：cv::getOptimalDFTSize()
DFT（傅里叶正变换）性能不是向量大小的单调函数。因此，当您计算两个数组的卷积或执行数组的频谱分析时，通常有必要在输入数据中填充零，以获得比原始数组转换速度快得多的更大的数组。大小为2的幂(2,4,8,16,32，…)的数组处理速度最快。但是，数组的大小是2、3和5的乘积(例如，300 = 55322)的处理效率也很高。

#include <opencv2/core.hpp>
函数说明：int cv::getOptimalDFTSize( int vecsize);
输入参数：		vecsize					给定向量。如果vecsize太大(非常接近INT_MAX)，则返回一个负数。
返回值：			N						返回大于或等于vecsize的最小数 N。

// 傅里叶变换
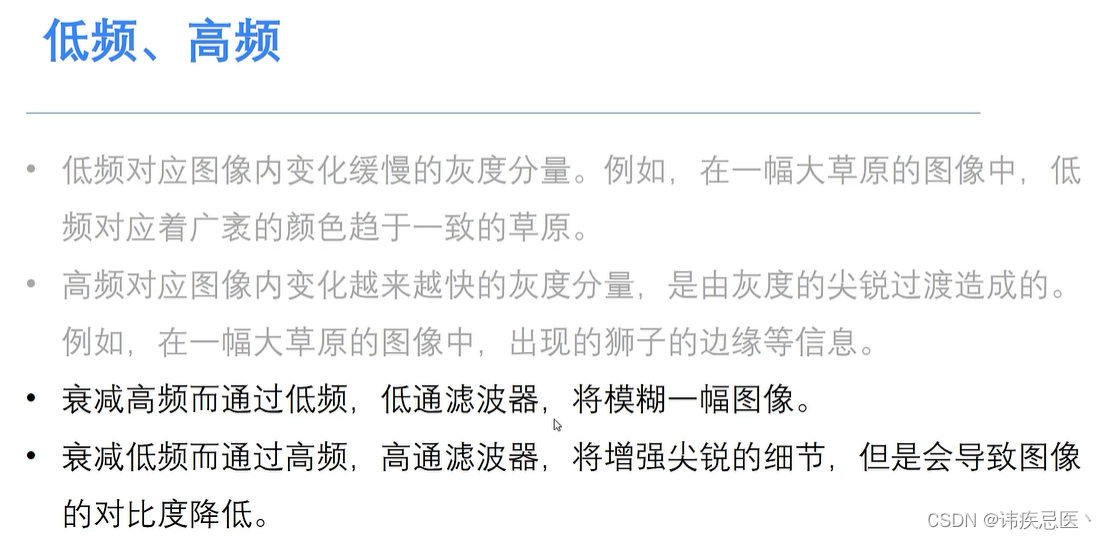
// 高频：变化剧烈的灰度分量，列如边界
// 低频：变化缓慢的灰度分量，例如一边大海
// 高频滤波器：只保留高频，会使得图像细节增强
// 低频滤波器：只保留低频，会使图像变模糊
void test_f()
{
	Mat img = imread("H:\\数据集\\已标注\\images\\datas\\all_datas\\1616003650999.jpg", IMREAD_GRAYSCALE);
	img.convertTo(img, CV_32F);

	// 数据准备
	// 离散傅里叶变换的运行速度与图像的大小有很大的关系，当图像的尺寸使2，3，5的整数倍时，计算速度最快
	// 为了达到快速计算的目的，经常通过添加新的边缘像素的方法获取最佳图像尺寸
	int w1 = getOptimalDFTSize(img.rows);
	int h1 = getOptimalDFTSize(img.cols);
	Mat padding;
	copyMakeBorder(img, padding, 0, w1-img.rows, 0, h1-img.cols, BORDER_CONSTANT,Scalar::all(0));
	
	// 执行傅里叶变换
	// 为傅立叶变换的结果分配存储空间
	// 将plannes数组组合成一个多通道的数组，两个同搭配，分别保存实部和虚部
	// 傅里叶变换的结果使复数，这就是说对于每个图像原像素值，会有两个图像值
	// 此外，频域值范围远远超过图象值范围，因此至少将频域储存在float中
	// 所以我们将输入图像转换成浮点型，并且多加一个额外通道来存储复数部分
	Mat planes[] = { Mat_<float>(padding),Mat::zeros(padding.size(),CV_32F) };
	Mat complexI;

	// planes[0]是实部，planes[1]是虚部
	merge(planes, 2,complexI);
	cout << complexI.size() << endl;
	cout << planes->size() << endl;

	dft(complexI, complexI, DFT_SCALE | DFT_COMPLEX_OUTPUT);
	split(complexI, planes);

	// 计算幅度普和相位谱
	Mat ph,mag,idft;
	phase(planes[0], planes[1], ph);
	magnitude(planes[0], planes[1], mag);

	// 重新排列傅里叶图像中的象限，使得原点位于图像中心
	int cx = mag.cols/2;
	int cy = mag.rows/2;
	Mat q1 = mag(Rect(0, 0, cx, cy));
	Mat q2 = mag(Rect(cx, 0, cx, cy));
	Mat q3 = mag(Rect(0, cy, cx, cy));
	Mat q4 = mag(Rect(cx, cy, cx, cy));

	// 变换左上角和右下角象限
	Mat tmp;
	q1.copyTo(tmp);
	q4.copyTo(q1);
	tmp.copyTo(q4);

	// 变换右上角和左下角
	q2.copyTo(tmp);
	q3.copyTo(q2);
	tmp.copyTo(q3);
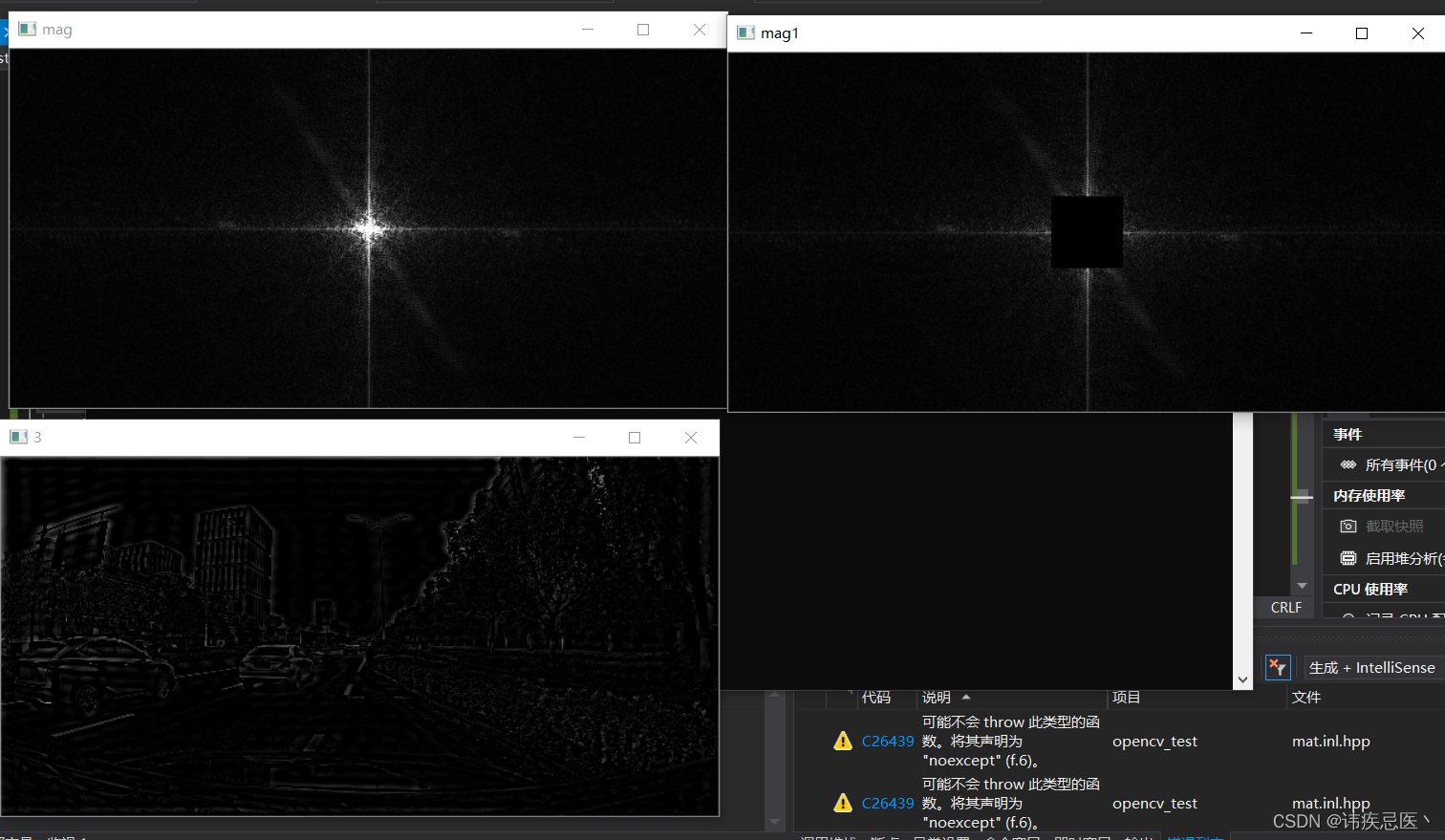
	imshow("mag", mag);

	// 对频域进行滤波操作
	// 对频域进行滤波操作 高频滤波器,也可以直接这句代替
	// mag(Rect(cx - 30, cy - 30, 30 * 2, 30 * 2)) = 0;
	// 如果像素距离图像中心的水平偏差（abs(i - mag.cols / 2)）或垂直偏差（abs(j - mag.rows / 2)）大于图像尺寸的十分之一（mag.cols / 10 或 mag.rows / 10），则满足条件。
	for (int i = 0; i < mag.cols; i++) {
		for (int j = 0; j < mag.rows; j++) {
			if (abs(i - mag.cols / 2) > mag.cols / 10 || abs(j - mag.rows / 2) > mag.rows / 10)
				// 0表示低通、1表示高通
				mag.at<float>(j, i) = 1;
		}
	}
	imshow("mag1", mag);

	//3.4、变换左上角和右下角象限
	q1.copyTo(tmp);
	q4.copyTo(q1);
	tmp.copyTo(q4);

	//3.5、变换右上角和左下角象限
	q2.copyTo(tmp);
	q3.copyTo(q2);
	tmp.copyTo(q3);

	//（4）傅里叶逆变换
	polarToCart(mag, ph, planes[0], planes[1]);
	//由幅度谱mag和相位谱ph恢复实部planes[0]和虚部planes[1]
	merge(planes, 2, idft);

	dft(idft, idft, cv::DFT_INVERSE | cv::DFT_REAL_OUTPUT);
	//  & -2 操作用于将宽度和高度向下取整为偶数
	img = idft(cv::Rect(0, 0, img.cols & -2, img.rows & -2));
	img.convertTo(img, CV_8U);
	imshow("3", img);
	waitKey(0);
}