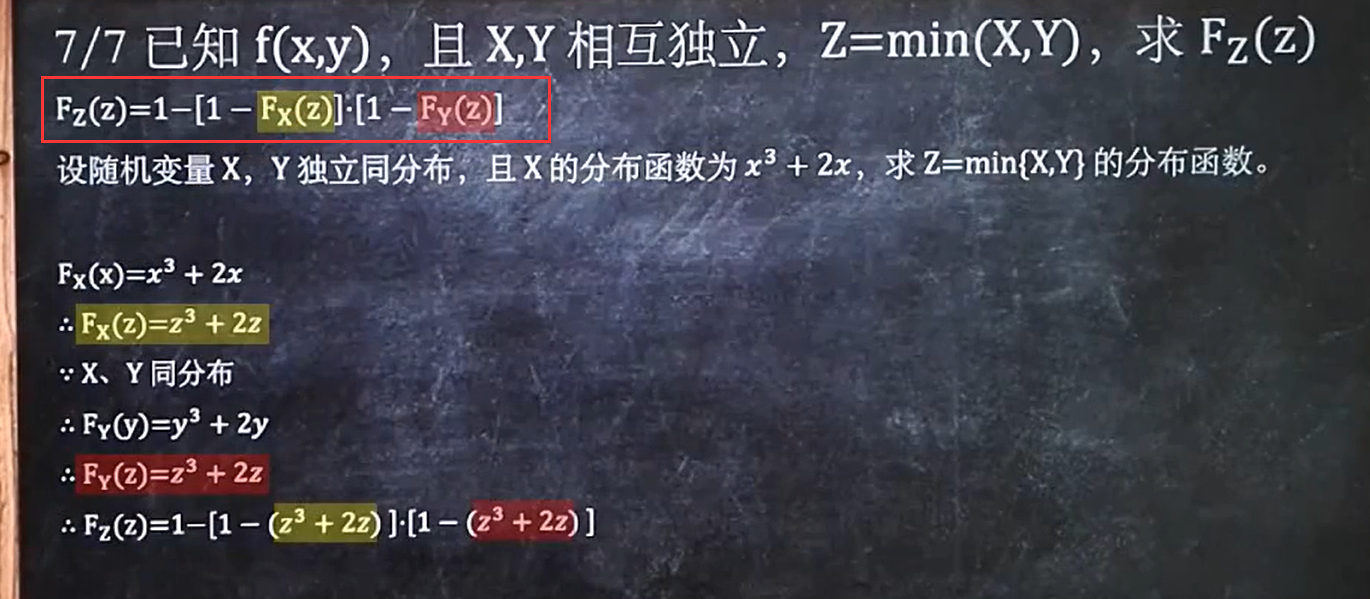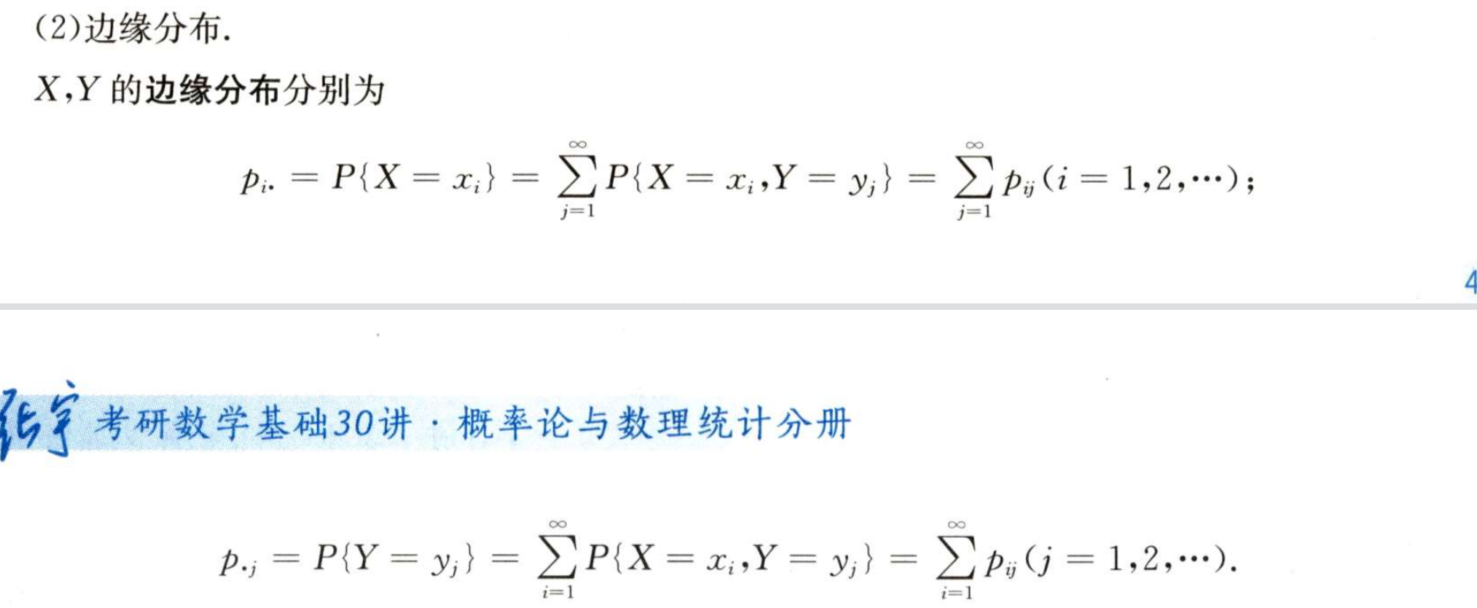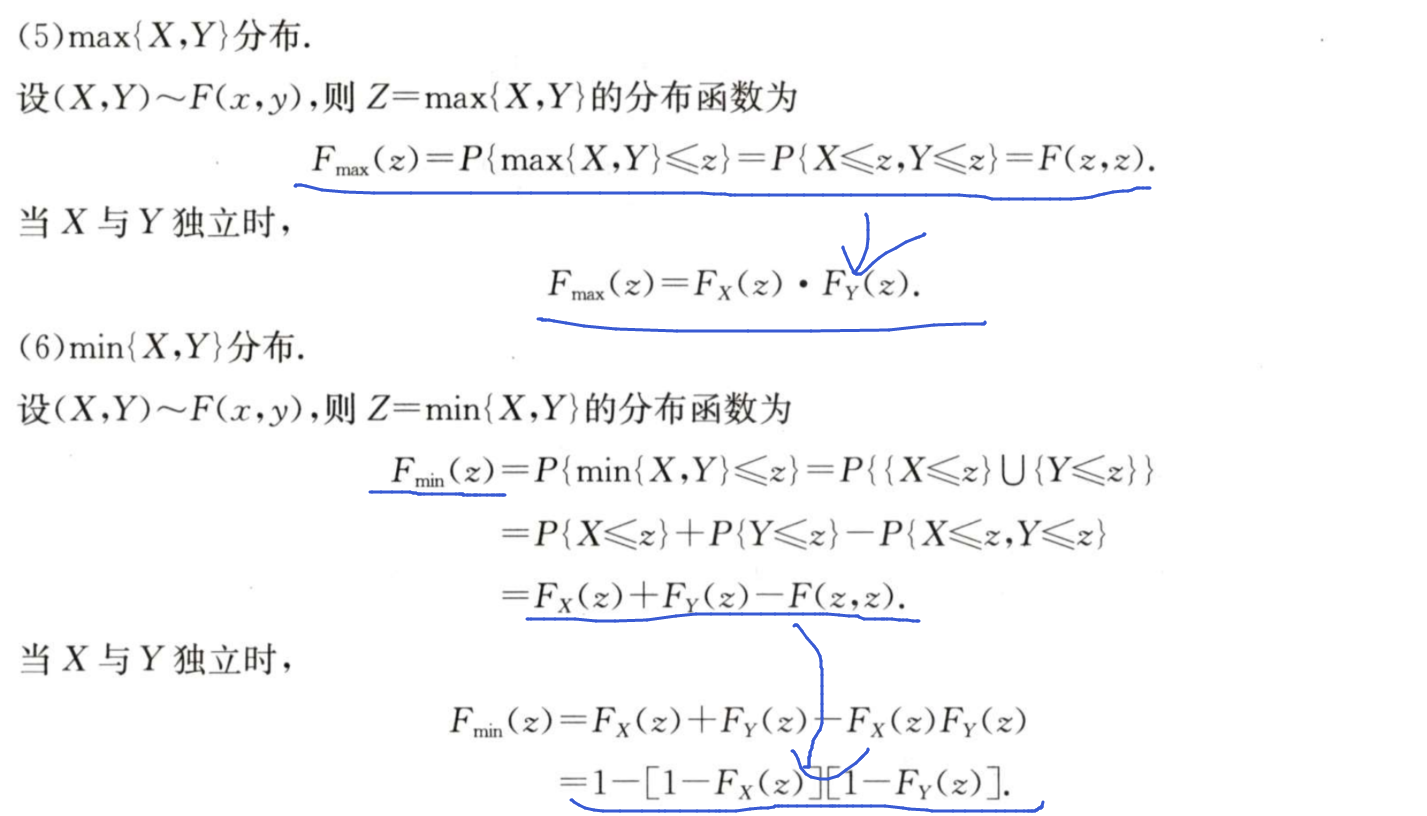6.连续型二维变量(下)
1/7 求边缘分布函数
边缘概率密度
边缘概率密度

2/7 求边缘密度函数
边缘概率密度

3/7 判断连续型二维变量的独立性
F(x,y) = Fx(X) * Fy(Y)那么X、Y互相独立
f(x,y) = fx(X) * fy(Y)那么X、Y互相独立
这种题目带入验证就可以了
先求出 fx(X) 和 fy(Y)带入计算验证就OK了
如何求出 fx(X) 和 fy(Y)在上一个题型说了

4/7 已知f(x,y),Z=X+Y,求fz(Z)
(卷积公式)
利用公式进行分类讨论就好啦

5/7 已知f(x,y),Z=x/y,求fz(Z)
同理4/7

6/7 已知f(x,y),且X,Y相互独立,Z=max(X,Y),求Fz(Z)
记住一个公式:Fz(Z) = Fx(Z)*Fy(Z)
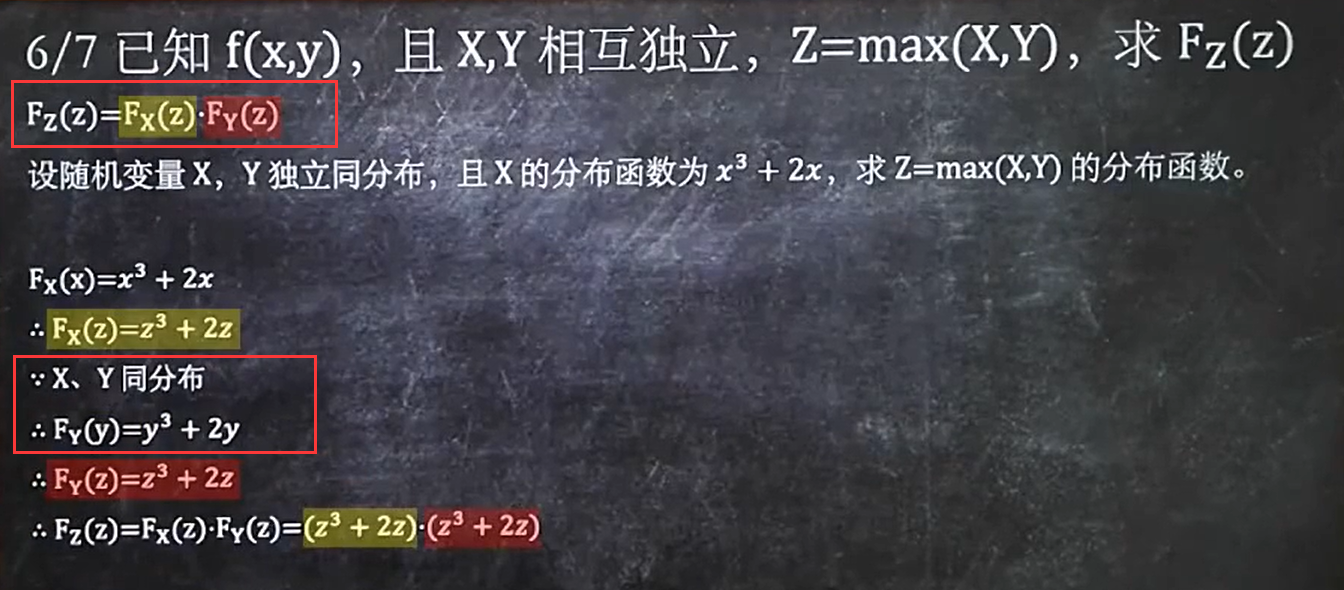
7/7 已知f(x,y),且X,Y相互独立,Z=min(X,Y),求Fz(Z)
同上面6/7的题目的公式不一样:Fz(Z)=1-[1-Fx(Z)]*[1-Fy(Z)]