Batch Normalization是谷歌研究员于2015年提出的一种归一化方法,其思想非常简单,一句话概括就是,对一个神经元(或者一个卷积核)的输出减去统计得到的均值,除以标准差,然后乘以一个可学习的系数,再加上一个偏置,这个过程就完成了。
一般而言BN层是在训练是更新均值 μ \mu μ、方差 σ 2 \sigma^2 σ2、 γ \gamma γ、 β \beta β。是一直在更新的。但是在推理的时候通常是要BN参数是固定的,均值方差是来自于训练样本的数据分布。(有想关注训练阶段BN层以及BN具体公式推导的可以观看吴恩达视频或者其他博客,此处就不再做详细介绍了)
因此在介绍BN融合时,训练阶段是conv+bn的构造,而在推理阶段才是convbn构造。接下来就简单介绍一下推理时convbn是如何进行的。
BN推理时怎么做
在推理时BN,计算公式可以变形为:
y
i
=
γ
x
i
−
μ
σ
2
+
ε
+
β
=
x
i
γ
σ
2
+
ε
+
(
β
−
γ
μ
σ
2
+
ε
)
y_i=\gamma\dfrac{x_i-\mu}{\sqrt{\sigma^2+\varepsilon}}+\beta=x_i\dfrac{\gamma}{\sqrt{\sigma^2+\varepsilon}}+(\beta-\dfrac{\gamma\mu}{\sqrt{\sigma^2+\varepsilon}})
yi=γσ2+εxi−μ+β=xiσ2+εγ+(β−σ2+εγμ)
而在方差均值都是固定值时,公式可以改写为
y
i
=
a
x
i
+
b
y_i = ax_i+b
yi=axi+b
其中
a
=
γ
σ
2
+
ε
,
b
=
β
−
γ
μ
σ
2
+
ε
a=\dfrac{\gamma}{\sqrt{\sigma^2+\varepsilon}},b=\beta-\dfrac{\gamma\mu}{\sqrt{\sigma^2+\varepsilon}}
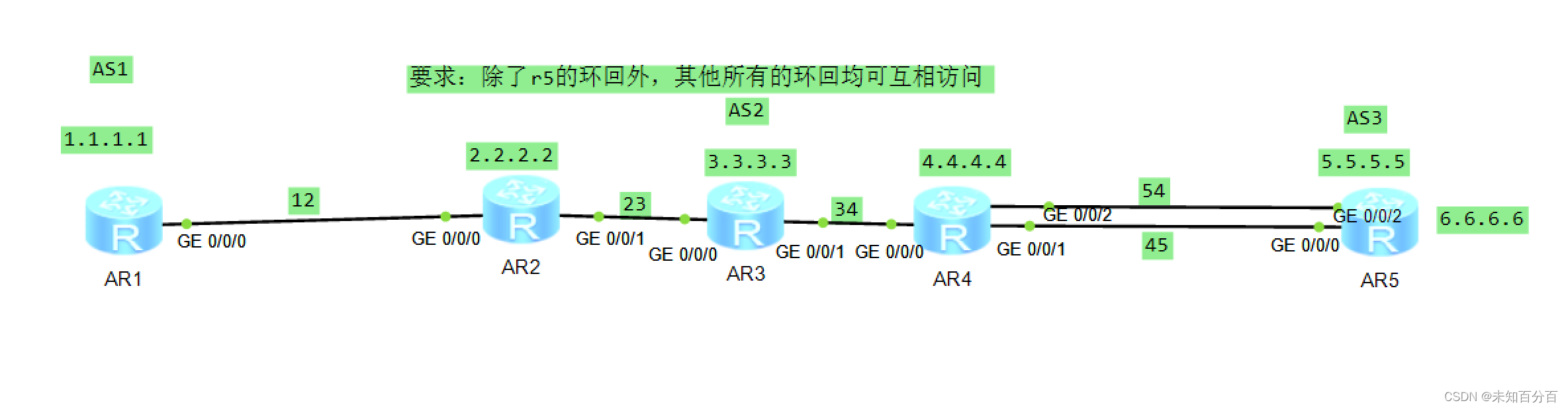
a=σ2+εγ,b=β−σ2+εγμ,接下来我们以一个三神经元作为输入的全连接网络为例进行过程分析,如下图:
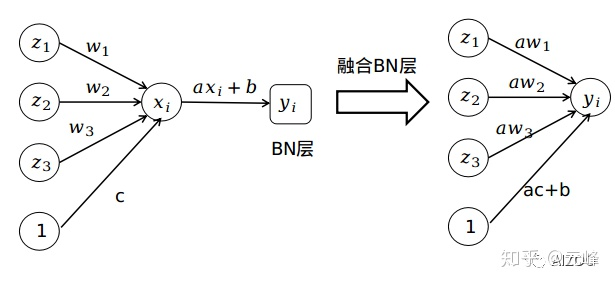
首先我们未融合BN层的全连接层的输入为:
x
i
=
w
1
⋅
z
1
+
w
2
⋅
z
2
+
w
3
⋅
z
3
+
c
x_i=w_1\centerdot z_1+w_2\centerdot z_2+w_3\centerdot z_3+c
xi=w1⋅z1+w2⋅z2+w3⋅z3+c
其中c为偏置,那么全连接+BN层的输出则为:
y
i
=
a
x
i
+
b
=
a
(
w
1
⋅
z
1
+
w
2
⋅
z
2
+
w
3
⋅
z
3
+
c
)
+
b
y_i=ax_i+b=a(w_1\centerdot z_1+w_2\centerdot z_2+w_3\centerdot z_3+c)+b
yi=axi+b=a(w1⋅z1+w2⋅z2+w3⋅z3+c)+b
也就是:
y
i
=
a
x
i
+
b
=
a
w
1
⋅
z
1
+
a
w
2
⋅
z
2
+
a
w
3
⋅
z
3
+
(
a
c
+
b
)
y_i=ax_i+b=aw_1\centerdot z_1+aw_2\centerdot z_2+aw_3\centerdot z_3+(ac+b)
yi=axi+b=aw1⋅z1+aw2⋅z2+aw3⋅z3+(ac+b)
而由于BN是一个线性的操作,也即一个缩放+一个偏移,也就完全可以把这个线性操作叠加到前面的全连接层或者卷积层。仅需将全连接层或者卷积层权重乘一个系数a,偏置从c变成ac+b就可以了。过程如右上图所示
在框架中进行融合的代码参考:AIZOO人工智能乐园
在此处需要注意的是融合BN仅限于Conv+BN或者是BN+Conv结构,中间不能加非线性层,例如Conv+ReLu+BN那就不行了。当然,一般结构都是Conv+BN+ReLu结构。而如何在部署的时候使用由于目前博主的水平未涉及暂不知,等以后操作过了进行更新。
Repvgg中使用
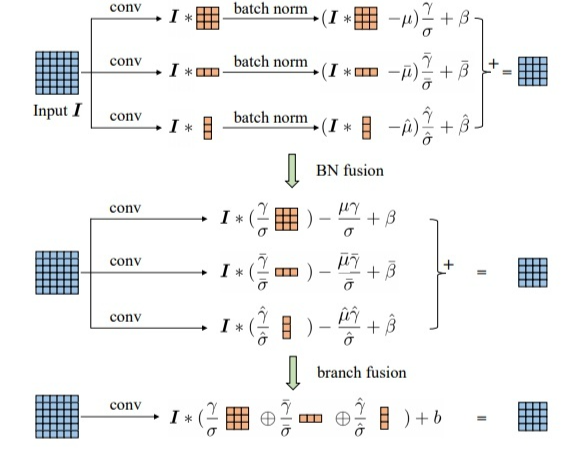
之所以要进行融合BN调研原因是因为在调研的时候遇到了Repvgg这篇文章,这篇文章有一个"结构重参数化"的思想,其具体过程如上图所示。
在Repvgg中推理过程会将三个分支进行合并融合,而在这过程中原文实验证明了将BN层和卷积层一起进行融合效果会更好。
本文参考链接:
进击的程序员
元峰
如有什么错误之处希望各位大佬给予指正,此文仅作个人记录所用,如有侵权请联系删除。