线性回归被定义为根据给定的变量集构建因变量和自变量之间关系的统计方法。在执行线性回归时,我们对计算响应变量的平均值感到好奇。相反,我们可以使用称为分位数回归的机制来计算或估计响应值的分位数(百分位数)值。例如,第30百分位、第50百分位等。
分位数回归
分位数回归是线性回归的扩展版本。分位数回归构建一组变量(也称为自变量)和分位数(也称为因变量)之间的关系。
在Python中执行分位数回归
计算分位数回归是一个逐步的过程。所有步骤详细讨论如下:
创建演示数据集
现在,让我们创建一个数据集。例如,我们正在创建一个数据集,其中包含20辆不同品牌的汽车的总行驶距离和总排放量的信息。
# Python program to create a dataset
# Importing libraries
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
np.random.seed(0)
# Specifying the number of rows
rows = 20
# Constructing Distance column
Distance = np.random.uniform(1, 10, rows)
# Constructing Emission column
Emission = 20 + np.random.normal(loc=0, scale=.25*Distance, size=20)
# Creating a dataframe
df = pd.DataFrame({'Distance': Distance, 'Emission': Emission})
df.head()
输出
Distance Emission
0 5.939322 22.218454
1 7.436704 19.618575
2 6.424870 20.502855
3 5.903949 18.739366
4 4.812893 16.928183
构建分位数回归
现在,我们将构建分位数回归模型,
- 行驶距离:作为预测变量
- 排放量:作为响应变量
现在,我们将利用这个模型来估计基于汽车行驶的总距离产生的排放的第70个百分位数。
# Python program to illustrate
# how to estimate quantile regression
# Importing libraries
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
np.random.seed(0)
# Number of rows
rows = 20
# Constructing Distance column
Distance = np.random.uniform(1, 10, rows)
# Constructing Emission column
Emission = 40 + Distance + np.random.normal(loc=0,
scale=.25*Distance,
size=20)
# Creating the data set
df = pd.DataFrame({'Distance': Distance,
'Emission': Emission})
# fit the model
model = smf.quantreg('Emission ~ Distance',
df).fit(q=0.7)
# view model summary
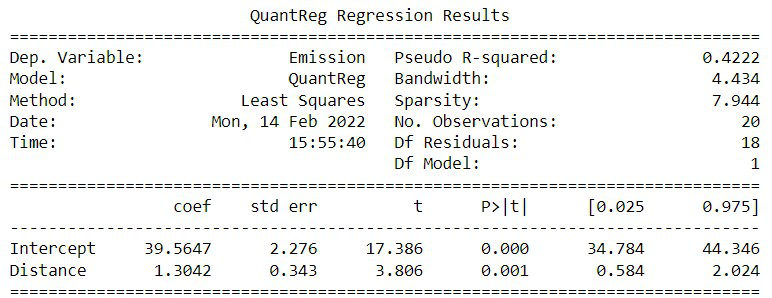
print(model.summary())
从该程序的输出中,可以推导出估计的回归方程为:
val = 39.5647 + 1.3042 * X (distance in km)
这意味着行驶X km的所有汽车的排放的第70百分位数预期为val。
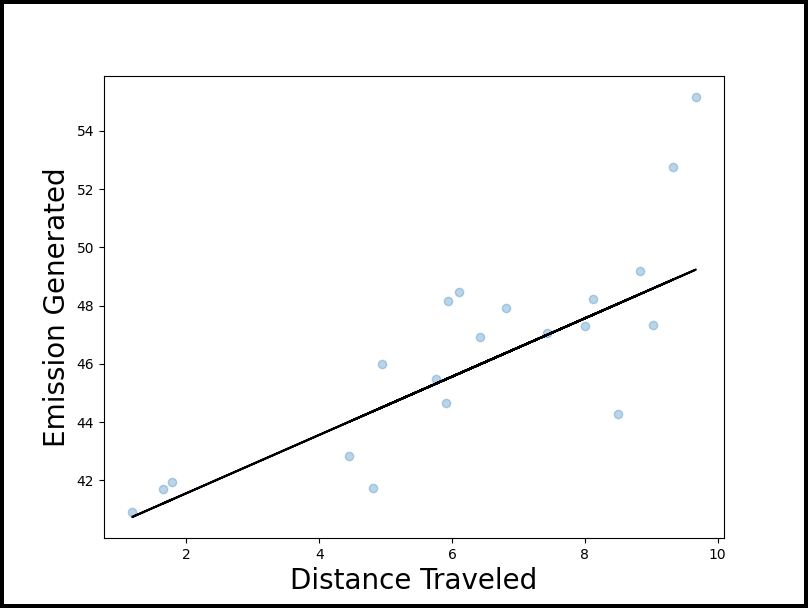
可视化分位数回归
为了可视化和理解分位数回归,我们可以使用散点图拟合分位数回归。
# Python program to visualize quantile regression
# Importing libraries
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
np.random.seed(0)
# Number of rows
rows = 20
# Constructing Distance column
Distance = np.random.uniform(1, 10, rows)
# Constructing Emission column
Emission = 40 + Distance + np.random.normal(loc=0,
scale=.25*Distance,
size=20)
# Creating a dataset
df = pd.DataFrame({'Distance': Distance,
'Emission': Emission})
# #fit the model
model = smf.quantreg('Emission ~ Distance',
df).fit(q=0.7)
# define figure and axis
fig, ax = plt.subplots(figsize=(10, 8))
# get y values
y_line = lambda a, b: a + Distance
y = y_line(model.params['Intercept'],
model.params['Distance'])
# Plotting data points with the help
# pf quantile regression equation
ax.plot(Distance, y, color='black')
ax.scatter(Distance, Emission, alpha=.3)
ax.set_xlabel('Distance Traveled', fontsize=20)
ax.set_ylabel('Emission Generated', fontsize=20)
# Save the plot
fig.savefig('quantile_regression.png')