39.组合总和
本题和 216.组合总和III 类似,但有几个区别:
- 没有元素个数限制:树的深度并不固定,因此递归终止条件有所变化
- 每个元素可以使用多次:下层递归的起始位置和上层相同(startIndex不需要改动)

class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
def backtrack(startIndex, path, currentSum):
# 和大于等于目标的时候终止
# 如果等于目标,还需要先收集
if currentSum >= target:
if currentSum == target:
result.append(path[:])
return
for i in range(startIndex, len(candidates)):
path.append(candidates[i])
currentSum += candidates[i]
# 下层递归的起始位置和本层相同
backtrack(i, path, currentSum)
path.pop()
currentSum -= candidates[i]
result = []
backtrack(startIndex = 0, path = [], currentSum = 0)
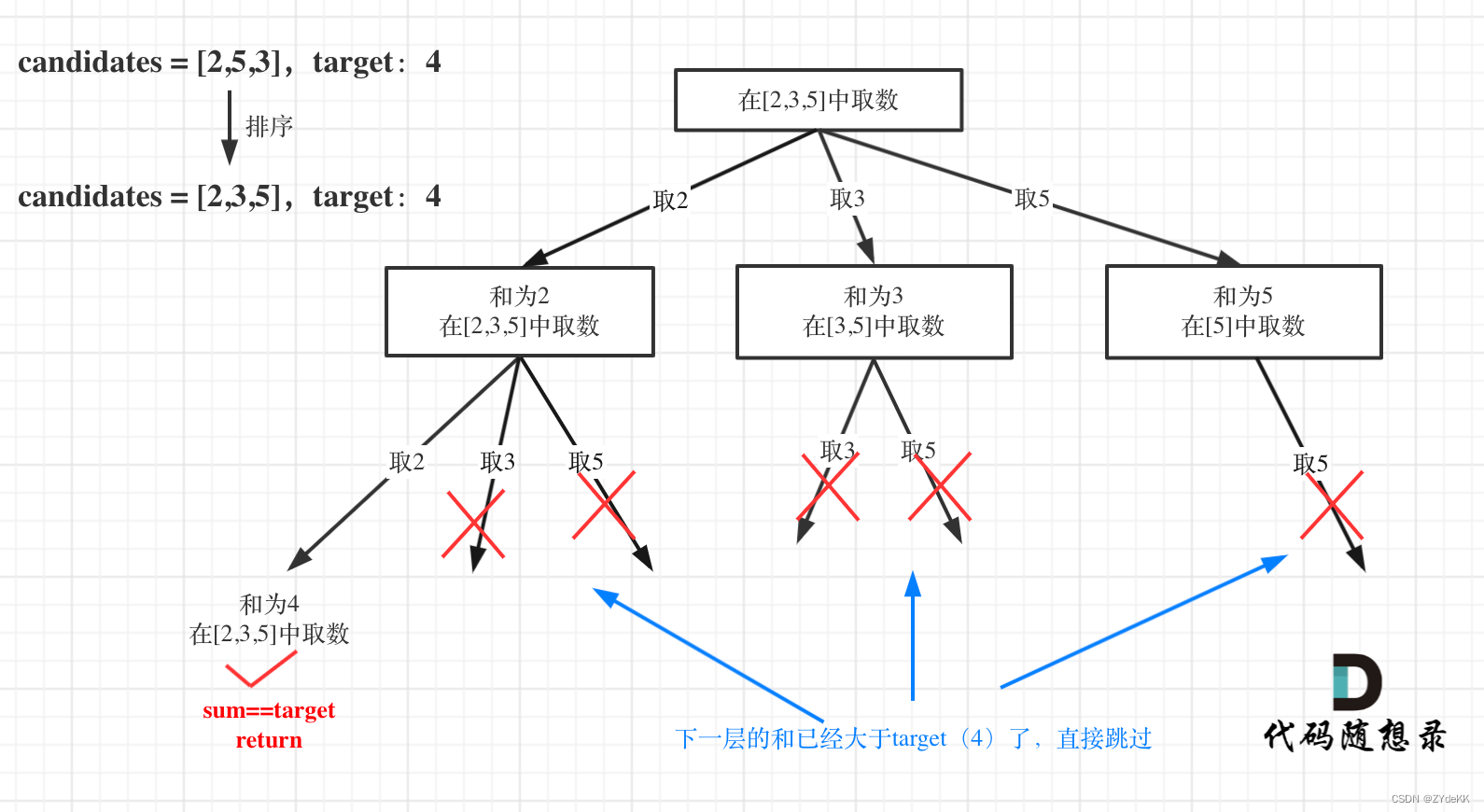
return result剪枝:如果我们事先对 candidates 排序,那么下一层递归的 currentSum 一定会更大,在此之前判断 currentSum 和 target 的判断可以实现剪枝。
为什么要排序?举个例子,假设总和为 4,那么 [2, 2] 符合条件,下一次搜索可能获得 [2, 1, 1] 也是符合条件的,如果排序则可以确保接下来搜索的元素更大,换句话说 [2, 1, 1] 一定在 [2, 2] 之前被找到。
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
def backtrack(startIndex, path, currentSum):
# 和大于等于目标的时候终止
# 如果等于目标,还需要先收集
if currentSum >= target:
if currentSum == target:
result.append(path[:])
return
for i in range(startIndex, len(candidates)):
# 剪枝:如果和已经超过,则不需要继续搜索
if currentSum + candidates[i] > target: continue
path.append(candidates[i])
currentSum += candidates[i]
# 下层递归的起始位置和本层相同
backtrack(i, path, currentSum)
path.pop()
currentSum -= candidates[i]
result = []
candidates.sort()
backtrack(startIndex = 0, path = [], currentSum = 0)
return result40.组合总和II
本题的关键是 candidates 中的元素可能重复,如果使用传统的方法递归,则结果很有可能包含重复组合。举个例子,假设 candidates = [1, 2, 2, 5],target = 3。当我们选择了 1,其递归出现 3个 分支:[1, 2]、[1, 2]、[1, 5],此时出现了重复组合。
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
def backtrack(startIndex, path, currentSum):
if currentSum >= target:
if currentSum == target:
result.append(path[:])
return
for i in range(startIndex, len(candidates)):
# 如果当前数字与前一个数字相同,并且不是遍历的第一个数字,则跳过以避免重复组合
if i > startIndex and candidates[i] == candidates [i-1]:
continue
# 剪枝
if currentSum + candidates[i] > target:
return
path.append(candidates[i])
currentSum += candidates[i]
backtrack(i + 1, path, currentSum)
path.pop()
currentSum -= candidates[i]
result = []
# 排序
candidates.sort()
backtrack(startIndex = 0, path = [], currentSum = 0)
return result131.分割回文串
本题可以理解为一个组合问题,我们组合不同的元素,判断是否为回文子串。
class Solution:
def partition(self, s: str) -> List[List[str]]:
# 双指针判断是否为回文串
def isPalindrome(subs):
left, right = 0, len(subs)-1
while left < right:
if subs[left] != subs[right]:
return False
left += 1
right -= 1
return True
def backtrack(startIndex, path):
# startIndex是我们的切割线
# 因此递归终止条件为切割到末尾
if startIndex >= len(s):
result.append(path[:])
return
for i in range(startIndex, len(s)):
# [startIndex, i]为我们的切割子串
if isPalindrome(s[startIndex: i+1]):
path.append(s[startIndex: i+1])
backtrack(i+1, path)
path.pop()
result = []
backtrack(startIndex = 0, path = [])
return result