一、背景

因为我是做机器人方向的，不可避免的涉及到视觉方向的内容，还有审稿的时候也会看到识别相关的内容，其中衡量识别效果的指标包括精度Precision和召回率Recall，虽然很好理解，但每次都记不住，趁这次机会详细纪录一下，并举一个通熟易懂的例子加深印象。

二、基础知识及解释

1.术语TP、TN 、FP 、FN

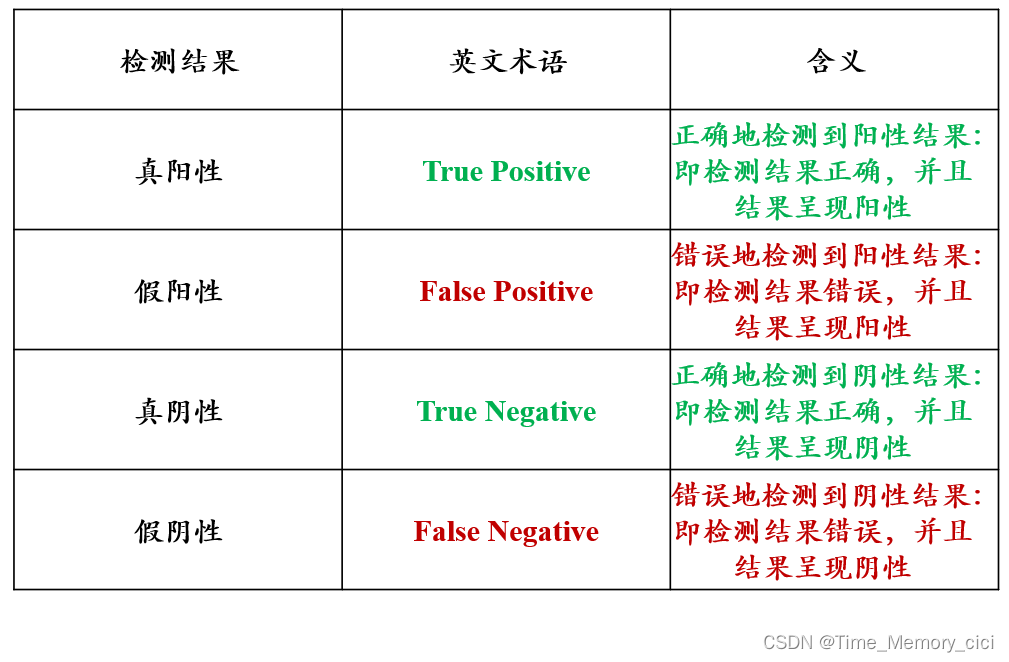
在机器学习和图像识别领域，我们经常会听到检测结果为"真阳性"、"假阴性"等说法。

“真”、"假"说的是检查结果的对错。”真“意味着检测结果是正确的，"假"意味着检测结果是错误的。
“阳性”、"阴性"说的是此次的检查结果。阳性，意味检测出了预定的目标。阴性，意味着没查出预定的目标。

2.混淆矩阵

混淆矩阵是机器学习领域中用于精度评价的一种标准格式，也被称为误差矩阵。混淆矩阵的每一行代表一个真实的标签，每一列代表一个预测的标签。矩阵的对角线元素表示模型正确分类的实例数，非对角线元素则表示模型错误分类的实例数。

在给个中文版本的：

3.精度（precision）

精度（precision），也叫查准率，就是在全部阳性预测中，正确预测结果所占的比例，计算公式为：

$\begin{array}{r}Precision=\frac{TP}{TP+FP}\end{array}$

通熟易懂的例子：一张图片有10个水果，其中苹果4个，西红柿6个。你用自己设计的识别算法检测后，苹果中的4个只检测出3个苹果，而有2个西红柿误识别为苹果，所以精度precision为：
$\begin{array}{r}Precision=\frac{3}{3+2}=0.6\end{array}$
总而言之，就是从实际苹果的数量中检测出苹果的数量 除以 识别到的苹果总数

4.召回率（Recall）

召回率（recall），也叫查全率，就是在全部阳性事件中，正确预测结果所占的比例，换句话说就是，它衡量模型正确识别出正样本的比例。计算公式为：

$\begin{array}{r}Recall=\frac{TP}{TP+FN}\end{array}$

通熟易懂的例子：一张图片有10个水果，其中苹果4个，西红柿6个。你用自己设计的识别算法检测后，苹果中的4个只检测出3个苹果，所以召回率为：
$\begin{array}{r}Recall=\frac{3}{4}=0.75\end{array}$
总而言之，就是全部苹果的数量中正确识别的个数。