目录
1、有序分数(usaco training 2.1)
2、正则问题(第八届蓝桥杯省赛C++ A组 & Java A组)
3、带分数(第四届蓝桥杯省赛Java A组/B组 & C++ B组/C组)
4、约数之和(《算法竞赛进阶指南》)
5、分形之城(《算法竞赛进阶指南》)
1、有序分数(usaco training 2.1)
给定一个整数 N,请你求出所有分母小于或等于 N,大小在 [0,1]范围内的最简分数,并按从小到大顺序依次输出。
例如,当 N=5 时,所有满足条件的分数按顺序依次为:
0/1,1/5,1/4,1/3,2/5,1/2,3/5,2/3,3/4,4/5,1/1
输入格式
共一行,包含一个整数 N。
输出格式
按照从小到大的顺序,输出所有满足条件的分数。
每个分数占一行,格式为 a/b,其中 a 为分子, b为分母。
数据范围
1≤N≤160
输入样例:
5
输出样例:
0/1
1/5
1/4
1/3
2/5
1/2
3/5
2/3
3/4
4/5
1/1思路:
用一个pair对来维护最小值和对应的分子分母,将所有情况枚举,为了避免重复我们要用一个set来确保没有重复的数值
这里要注意进入递归函数要直接进入最里面的一层开始往上递归,这样就可以做到所有分数的都是最简分数式
代码:
#include<bits/stdc++.h>
using namespace std;
int n;
typedef pair<int,int> PII;
typedef pair<double,PII> PDP;
const int N=1e5;
vector<PDP>res;
unordered_set<double>cnt;
void work(int n)
{
if(n==0)return ;
work(n-1);
for(int i=n-1;i>0;i--)
{
double number=(double)i/n;
if(cnt.find(number)!=cnt.end())continue;
cnt.insert(number);
PII t={i,n};
res.push_back({number,t});
}
}
bool cmp(PDP a,PDP b)
{
return a.first<b.first;
}
int main()
{
cin>>n;
res.push_back({0,{0,1}});
res.push_back({1,{1,1}});
work(n);
sort(res.begin(),res.end(),cmp);
for(auto t:res)
{
cout<<t.second.first<<"/"<<t.second.second<<endl;
}
return 0;
} 2、正则问题(第八届蓝桥杯省赛C++ A组 & Java A组)
考虑一种简单的正则表达式:
只由 x ( ) | 组成的正则表达式。
小明想求出这个正则表达式能接受的最长字符串的长度。
例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是: xxxxxx,长度是6。
输入格式
一个由x()|组成的正则表达式。
输出格式
输出所给正则表达式能接受的最长字符串的长度。
数据范围
输入长度不超过100,保证合法。
输入样例:
((xx|xxx)x|(x|xx))xx
输出样例:
6思路:
递归+回溯
代码:
#include<bits/stdc++.h>
using namespace std;
int k=0;
string s;
//((xx|xxx)x|(x|xx))xx
//6
int dfs()
{
int res=0;
while(k<s.size())
{
if(s[k]=='(')
{
k++;
res+=dfs();
k++;
}
else if(s[k]==')')
{
break;
}
else if(s[k]=='|')
{
k++;
res=max(res,dfs());
}
else
{
k++;
res++;
}
}
return res;
}
int main()
{
cin>>s;
int res=dfs();
cout<<res;
return 0;
}3、带分数(第四届蓝桥杯省赛Java A组/B组 & C++ B组/C组)
100可以表示为带分数的形式:100=3+69258/714
还可以表示为:100=82+3546/197
注意特征:带分数中,数字 1∼9分别出现且只出现一次(不包含 0)。
类似这样的带分数,100 有 11种表示法。
输入格式
一个正整数。
输出格式
输出输入数字用数码 1∼9 不重复不遗漏地组成带分数表示的全部种数。
数据范围
1≤N<1e6
输入样例1:
100
输出样例1:
11
输入样例2:
105
输出样例2:
6思路:
由于c++的/并不准确,我们把除法转化为乘法,再进行枚举(n=a+b/c转化为nc=ac+b)
从而我们枚举出a和c就可以算出b,b=nc-ac;
用had_use记录用过的数,ever用来在不影响并行递归的情况下把当前情况递归下去(不破坏原来的记录)
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=600;
//typedef long long LL;
int ever[N],had_use[N];
//数组放在最上面,acwing平台由于放在了ans下面导致输出结果错误
int ans=0;
int n;
//n=a+b/c
//nc=ac+b
//b=nc-ac 只要推出来的b满足条件,a和c都满足条件则答案+1
bool check(int a,int c)
{
int b=n*c-a*c;
if(!a || !c || !b)return false;
memcpy(ever,had_use,sizeof had_use);//基于现有的情况下,不破坏原来的数组
//那就拷贝一份,既能在原来之上操作,又能不破坏原来的记录
while(b)//取出每一位,用来更新用过的数字
{
int t=b%10;
b/=10;
if(!t || ever[t])return false;
ever[t]=1;
}
for(int i=1;i<=9;i++)if(!ever[i])return false;
return true;
}
void dfs_c(int x,int a,int c)
{
if(x>=10)return ;
if(check(a,c))ans++;
for(int i=1;i<=9;i++)
{
if(!had_use[i])
{
had_use[i]=1;
dfs_c(x+1,a,c*10+i);
had_use[i]=0;//回溯,避免下次的递归中出现错误
}
}
}
void dfs_a(int x,int a)
{
if(a>=n)return;
if(a)dfs_c(x,a,0);//如果a满足条件,那么枚举c然后判断是否是成立的
//0是c的大小
for(int i=1;i<=9;i++)//枚举一下当前能用哪些数字
{
if(!had_use[i])
{
had_use[i]=1;
dfs_a(x+1,a*10+i);
had_use[i]=0;//恢复现场,回溯一下
}
}
}
int main()
{
//cout<<714*97;
cin>>n;
dfs_a(0,0);//第一个表示当前用了多少个数字,第二个参数表示当前的a是多少
cout<<ans;
return 0;
}4、约数之和(《算法竞赛进阶指南》)
假设现在有两个自然数 A 和 B,S 是A的B次方的所有约数之和。
请你求出 S mod9901 的值是多少。
输入格式
在一行中输入用空格隔开的两个整数 A 和 B。
输出格式
输出一个整数,代表 Smod9901 的值。
数据范围
0≤A,B≤5×1e7
输入样例:
2 3
输出样例:
15
注意: A 和 B不会同时为 0。
思路:
分解质因数,把每个质因数的从第0项到最高次数的和乘起来就是约数之和
由于是求A的B次方的约数之和,我们可以先把A分解质因数,次方B可以后来再给到质因数的次方上

代码:
#include<bits/stdc++.h>
using namespace std;
const int MOD=9901;
typedef long long LL;
LL a,b;
LL res=0;
unordered_map<int,int>primes;
LL quickmi(LL a,LL b)
{
LL res=1;
while(b)
{
if(b&1)res=res*a%MOD;
a=a*a%MOD;
b=b>>1;
}
return res%MOD;
}
void divide(LL x)
{
for(int i=2;i<=x/i;i++)
{
if(x%i==0)
{
while(x%i==0)
{
primes[i]++;
x/=i;
}
}
}
if(x>1)primes[x]++;
}
//求p0+....pk-1
LL sum(LL p,LL k)
{
if(k==1)return 1;
if(k%2==0)return (LL)(quickmi(p,k/2)+1)*sum(p,k/2)%MOD;
return (LL)(quickmi(p,k-1)+sum(p,k-1))%MOD;
}
int main()
{
cin>>a>>b;
divide(a);
LL res=1;
for(auto prime :primes)
{
int p=prime.first;
int k=prime.second*b;//p的次数
res=(LL)res*sum(p,k+1)%MOD;//求约数之和
}
if(!a)res=0;
cout<<res<<endl;
return 0;
}5、分形之城(《算法竞赛进阶指南》)
城市的规划在城市建设中是个大问题。
不幸的是,很多城市在开始建设的时候并没有很好的规划,城市规模扩大之后规划不合理的问题就开始显现。
而这座名为 Fractal 的城市设想了这样的一个规划方案,如下图所示:
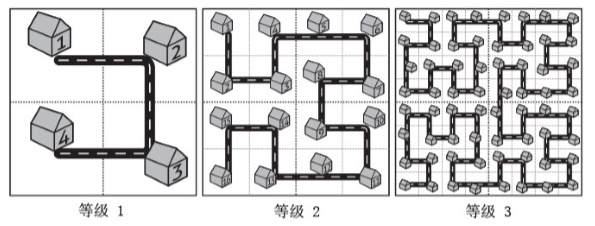
当城区规模扩大之后,Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围,提升城市的等级。
对于任意等级的城市,我们把正方形街区从左上角开始按照道路标号。
虽然这个方案很烂,Fractal 规划部门的人员还是想知道,如果城市发展到了等级 N,编号为 A 和 B 的两个街区的直线距离是多少。
街区的距离指的是街区的中心点之间的距离,每个街区都是边长为 10 米的正方形。
输入格式
第一行输入正整数 n,表示测试数据的数目。
以下 n 行,输入 n 组测试数据,每组一行。
每组数据包括三个整数 N,A,B表示城市等级以及两个街区的编号,整数之间用空格隔开。
输出格式
一共输出 n 行数据,每行对应一组测试数据的输出结果,结果四舍五入到整数。
数据范围
1≤N≤31
1≤A,B≤2**2N
1≤n≤1000
输入样例:
3
1 1 2
2 16 1
3 4 33
输出样例:
10
30
50 思路:
我们要知道第n等级城市的信息就要知道n-1等级的(n-1等级的城市可以通过旋转变换得出n等级城市的坐标信息),递归下去,最后算出街区中心坐标然后进行勾股定理即可,注意要乘上单位长度(本代码为5)
代码:
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
typedef pair<LL,LL> PLL;
#define x first
#define y second
PLL calc(LL n,LL m)
{
//n代表城市等级
//m代表坐标,从0开始计数
if(n==0)return {0,0};
LL len = 1ll <<(n-1);//本等级内象限的边长/2
LL cnt=1ll<<(2*n-2);//上一等级的容量
PLL pos = calc(n - 1, m % cnt); // 上一等级的坐标信息
LL x=pos.x,y=pos.y;
int z=m/cnt;//处于哪个象限
if (z == 0)
return { - y - len, - x + len };
// 右上象限更换原点(x+len,y+len)
else if (z == 1)
return { x + len, y + len };
// 右下象限更换原点(x+len,y-len)
else if (z == 2)
return { x + len, y - len };
// 左下象限逆转90°(-y,x)沿y对称(y,x)更换原点(y-len,x-len)
return { y - len, x - len };
}
int main()
{
int N;
cin >> N;
while (N --)
{
LL n, m1, m2;
cin >> n >> m1 >> m2;
PLL pos1 = calc(n, m1 - 1);
PLL pos2 = calc(n, m2 - 1);
double x = (double) (pos1.first - pos2.first);
double y = (double) (pos1.second - pos2.second);
//单位长度要乘五
printf("%.0lf\n", sqrt(x * x + y * y) * 5);
}
return 0;
}