【数据结构】深入理解AVL树：实现和应用

news2024/12/23 20:49:01

AVL树是一种自平衡的二叉搜索树，它能够保持良好的平衡性质，使得在最坏情况下的时间复杂度也能保持在对数级别。本文将深入介绍AVL树的原理、实现和应用，并通过示例代码演示其基本操作。

文章目录

  • 什么是AVL树？
  • AVL树的实现
    • 在AVL树中插入值为data的节点实现：
    • AVL树的旋转
      • 右单旋
      • 左单旋
      • 左右双旋
      • 右左双旋
  • AVL树的应用
  • 完整代码
  • 总结

什么是AVL树？

AVL树是由两位苏联数学家Adelson-Velsky和Landis于1962年发明的，它的特点是能够在插入和删除节点时自动调整树的结构，以保持树的平衡性。在AVL树中，任意节点的左右子树高度差不超过1，这就保证了整棵树的高度始终保持在对数级别，从而保证了插入、删除和查找等操作的高效性。

AVL树的实现

以下是一个C++实现的AVL树的基本结构和操作示例：

template<class T>
struct AVLTreeNode
{
	AVLTreeNode(const T& data = T())
	: _pLeft(nullptr)
	, _pRight(nullptr)
	, _pParent(nullptr)
	, _data(data)
	, _bf(0)
	{}

	AVLTreeNode<T>* _pLeft;
	AVLTreeNode<T>* _pRight;
	AVLTreeNode<T>* _pParent;
	T _data;
	int _bf;   // 节点的平衡因子
};


// AVL: 二叉搜索树 + 平衡因子的限制
template<class T>
class AVLTree
{
	typedef AVLTreeNode<T> Node;
public:
	AVLTree()
		: _pRoot(nullptr)
	{}

    // 在AVL树中插入值为data的节点
	bool Insert(const T& data);
    
    // AVL树的验证
	bool IsAVLTree()
	{
		return _IsAVLTree(_pRoot);
	}

private:
    // 根据AVL树的概念验证pRoot是否为有效的AVL树
	bool _IsAVLTree(Node* pRoot);
	size_t _Height(Node* pRoot);
    // 右单旋
	void RotateR(Node* pParent);
    // 左单旋
	void RotateL(Node* pParent);
    // 右左双旋
	void RotateRL(Node* pParent);
    // 左右双旋
	void RotateLR(Node* pParent);

private:
	Node* _pRoot;
};

在AVL树中插入值为data的节点实现：

// 在AVL树中插入值为data的节点
bool Insert(const T& data) {
	// 插入节点
	if (_pRoot == nullptr) {
		_pRoot = new Node(data);
		return true;
	}

	Node* pParent = nullptr;
	Node* pCur = _pRoot;
	while (pCur) {
		pParent = pCur;
		if (data < pCur->_data)
			pCur = pCur->_pLeft; // 往左子树查找
		else if (data > pCur->_data) 
			pCur = pCur->_pRight; // 往右子树查找
		else
			return false; // 重复值不插入
	}

	// 创建新节点
	pCur = new Node(data);
	if (data < pParent->_data)
		pParent->_pLeft = pCur;
	else
		pParent->_pRight = pCur;

	pCur->_pParent = pParent;

	// 插入节点后，更新平衡因子并进行平衡处理
	while (pParent) {
		if (pCur == pParent->_pLeft) // 更新节点在左子树
			--pParent->_bf; // 更新父节点的平衡因子
		else
			++pParent->_bf; // 更新父节点的平衡因子

		if (0 == pParent->_bf) // 如果平衡旋转结束
			break;

			// 如果父节点的bf==1或-1，则不需要调整，直接向上更新即可
		if (1 == pParent->_bf || -1 == pParent->_bf) {
			pCur = pParent;
			pParent = pParent->_pParent;
		} 
		else { // 父节点不平衡，需要旋转调整
			if (pParent->_bf == 2) {
				if (pCur->_bf == 1) // LL型
					// 左单旋
					RotateL(pParent);
				else // LR型
					// 先左旋后右旋
					RotateRL(pParent);
			}
			else {
				if (pCur->_bf == -1) // RR型
					// 右单旋
					RotateR(pParent);
				else // RL型
					// 先左旋后右旋
					RotateLR(pParent);
			}
			break;
		}
	}
	return true;
}

AVL树的旋转

AVL树的平衡是通过维护每个节点的平衡因子来实现的。平衡因子指的是节点的左子树高度减去右子树高度的差值，其取值范围为-1、0和1。当平衡因子的绝对值超过1时，AVL树就需要进行旋转操作来重新平衡。

右单旋

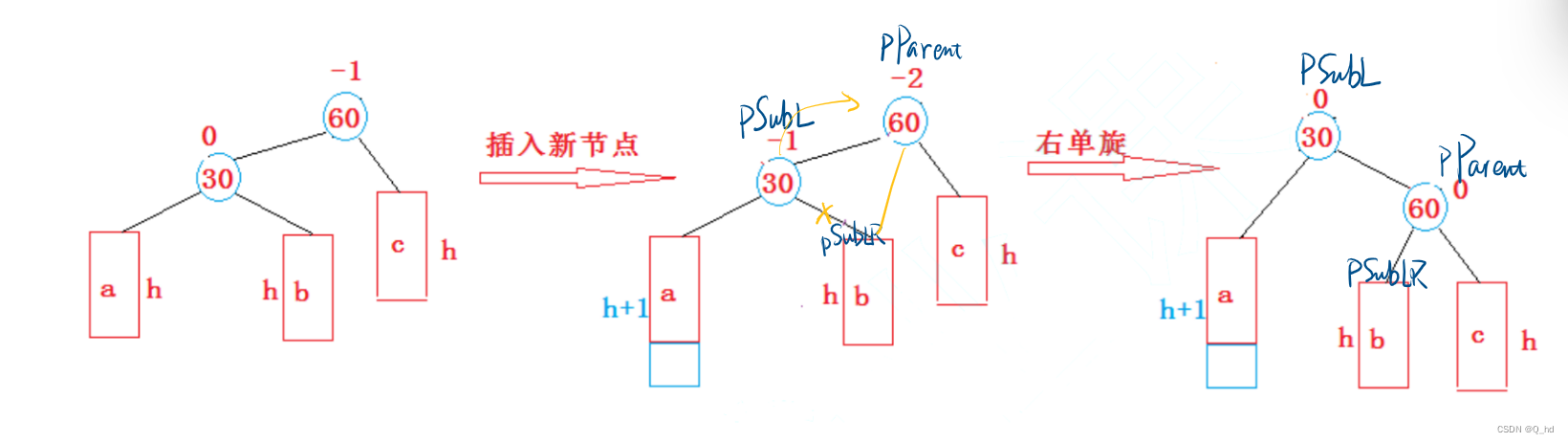
在这里插入图片描述

// 右单旋
	void RotateR(Node* pParent) {
		Node* pSubL = pParent->_pLeft;
		Node* pSubLR = pSubL->_pRight;

		// 右旋
		pParent->_pLeft = pSubLR;
		if (pSubLR)
			pSubLR->_pParent = pParent;

		pSubL->_pRight = pParent;
		pSubL->_pParent = pParent->_pParent;
		pParent->_pParent = pSubL;

		if (pParent == _pRoot)
			_pRoot = pSubL;
		else {
			if (pSubL->_pParent->_pLeft == pParent)
				pSubL->_pParent->_pLeft = pSubL;
			else
				pSubL->_pParent->_pRight = pSubL;
		}

		pParent->_bf = pSubL->_bf = 0;
	}

左单旋

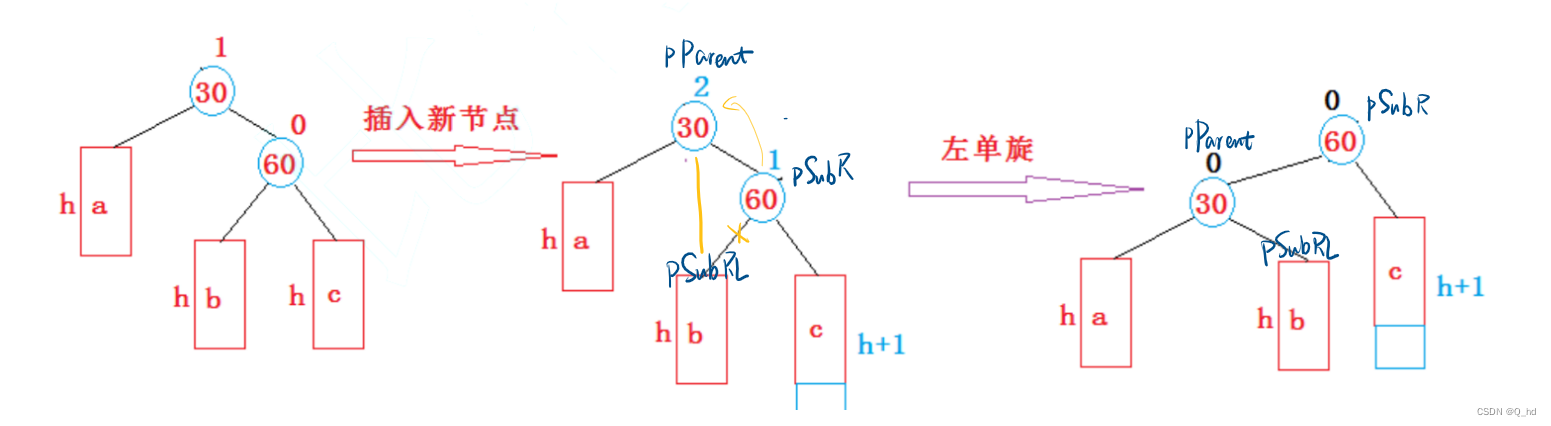
在这里插入图片描述

// 左单旋
void RotateL(Node* pParent) {
	Node* pSubR = pParent->_pRight;
	Node* pSubRL = pSubR->_pLeft;

	// 左旋
	pParent->_pRight = pSubRL;
	if (pSubRL)
		pSubRL->_pParent = pParent;

	pSubR->_pLeft = pParent;
	pSubR->_pParent = pParent->_pParent;
	pParent->_pParent = pSubR;

	if (pParent == _pRoot)
		_pRoot = pSubR;
	else
	{
		if (pSubR->_pParent->_pLeft == pParent)
			pSubR->_pParent->_pLeft = pSubR;
		else
			pSubR->_pParent->_pRight = pSubR;
	}

	pParent->_bf = pSubR->_bf = 0;
}

左右双旋

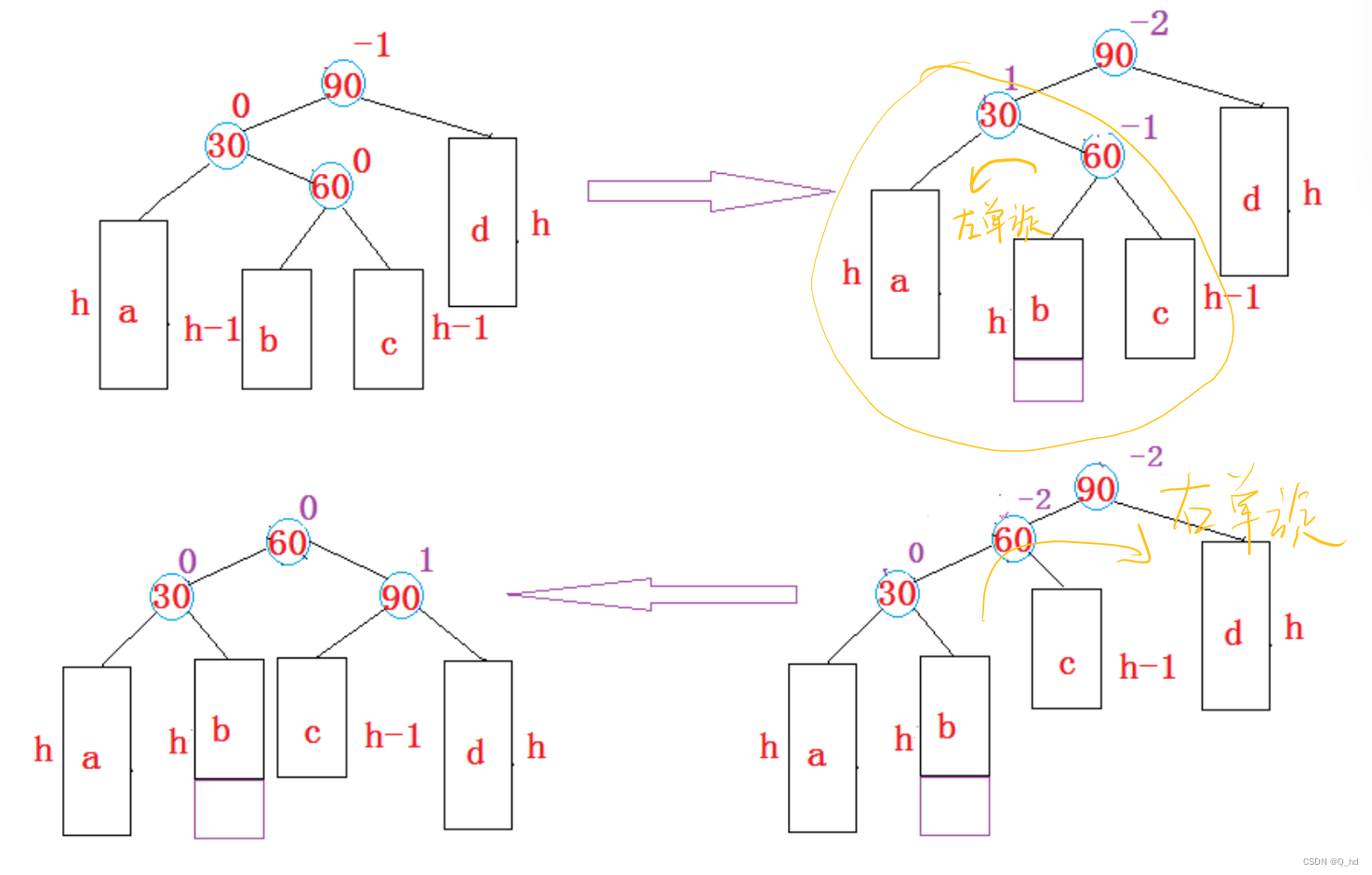
在这里插入图片描述

// 左右双旋
void RotateLR(Node* pParent) {
	// 先左旋后右旋
	Node* pSubL = pParent->_pLeft;
	Node* pSubLR = pSubL->_pRight;

	// 旋转之前，保存pSubLR的平衡因子，旋转完成之后，需要根据该平衡因子来调整其他节点的平衡因子
	int bf = pSubLR->_bf;

	// 进行左单旋
	RotateL(pParent->_pLeft);

	// 进行右单旋
	RotateR(pParent);
	if (1 == bf)
		pSubL->_bf = -1;
	else if (-1 == bf)
		pParent->_bf = 1;
}

右左双旋

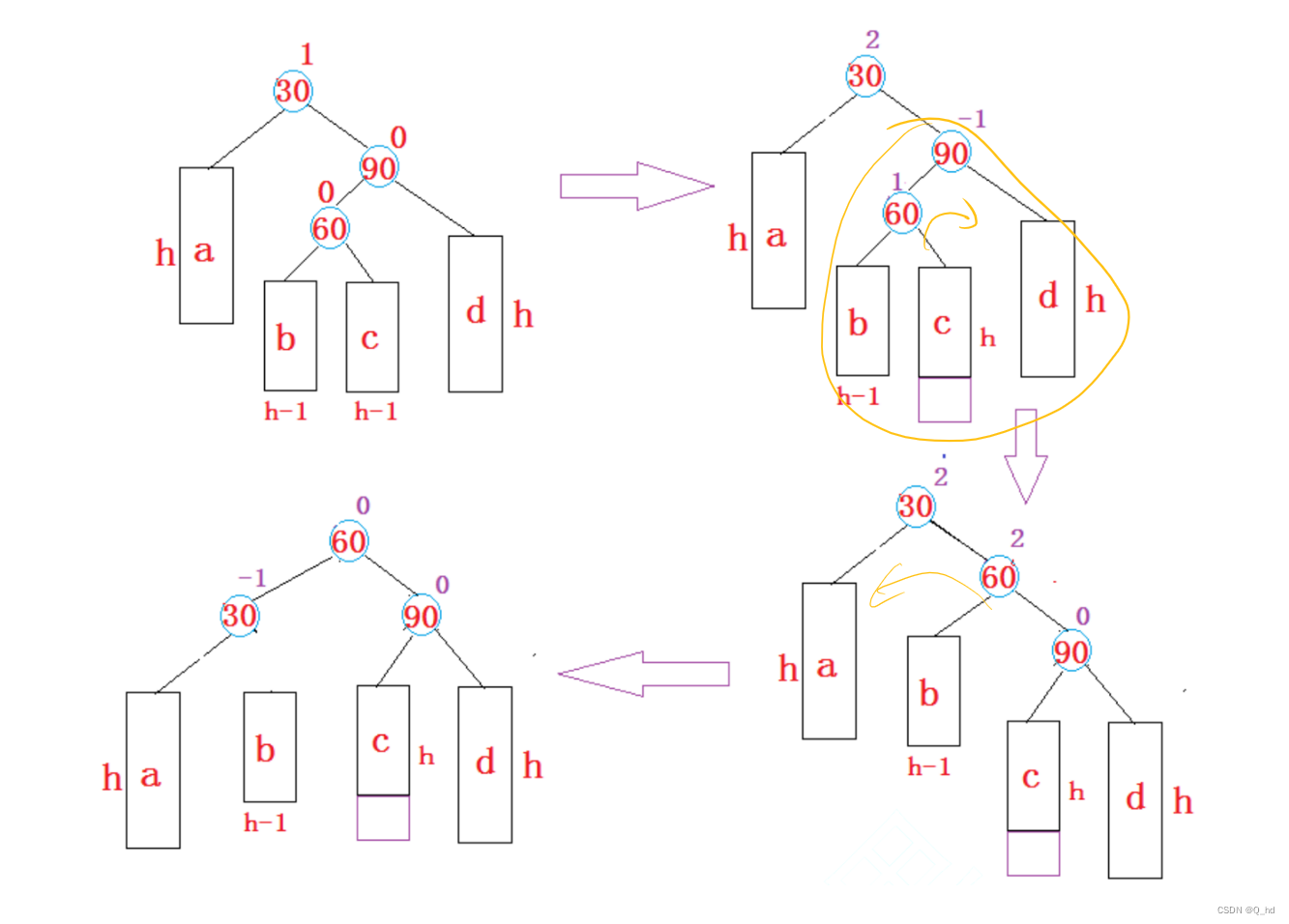
在这里插入图片描述

// 右左双旋
void RotateRL(Node* pParent) {
	// 先右旋后左旋
	Node* pSubR = pParent->_pRight;
	Node* pSubRL = pSubR->_pLeft;

	// 旋转之前，保存pSubRL的平衡因子，旋转完成之后，需要根据该平衡因子来调整其他节点的平衡因子
	int bf = pSubRL->_bf;

	// 进行右单旋
	RotateR(pParent->_pRight);

	//进行左单旋
	RotateL(pParent);
	if (1 == bf)
		pParent->_bf = -1;
	else if (-1 == bf)
		pSubR->_bf = 1;
}

AVL树的应用

AVL树由于其高效的插入、删除和查找操作，在计算机科学领域有着广泛的应用。例如，在数据库系统中，AVL树常被用作索引结构，用于加速数据的检索操作；在编译器的符号表实现中，也可以使用AVL树来存储和查找变量信息。

完整代码

// AVLTree.h
#include <iostream>
using namespace std;
template<class T>
struct AVLTreeNode
{
	AVLTreeNode(const T& data = T())
		: _pLeft(nullptr)
		, _pRight(nullptr)
		, _pParent(nullptr)
		, _data(data)
		, _bf(0)
	{}

	AVLTreeNode<T>* _pLeft;
	AVLTreeNode<T>* _pRight;
	AVLTreeNode<T>* _pParent;
	T _data;
	int _bf;   // 节点的平衡因子
};


// AVL: 二叉搜索树 + 平衡因子的限制
template<class T>
class AVLTree
{
	typedef AVLTreeNode<T> Node;
public:
	AVLTree()
		: _pRoot(nullptr)
	{}

	// 在AVL树中插入值为data的节点
	bool Insert(const T& data) {
		// 插入节点
		if (_pRoot == nullptr) {
			_pRoot = new Node(data);
			return true;
		}

		Node* pParent = nullptr;
		Node* pCur = _pRoot;
		while (pCur) {
			pParent = pCur;
			if (data < pCur->_data)
				pCur = pCur->_pLeft; // 往左子树查找
			else if (data > pCur->_data) 
				pCur = pCur->_pRight; // 往右子树查找
			else
				return false; // 重复值不插入
		}

		// 创建新节点
		pCur = new Node(data);
		if (data < pParent->_data)
			pParent->_pLeft = pCur;
		else
			pParent->_pRight = pCur;

		pCur->_pParent = pParent;

		// 插入节点后，更新平衡因子并进行平衡处理
		while (pParent) {
			if (pCur == pParent->_pLeft) // 更新节点在左子树
				--pParent->_bf; // 更新父节点的平衡因子
			else
				++pParent->_bf; // 更新父节点的平衡因子

			if (0 == pParent->_bf) // 如果平衡旋转结束
				break;

				// 如果父节点的bf==1或-1，则不需要调整，直接向上更新即可
			if (1 == pParent->_bf || -1 == pParent->_bf) {
				pCur = pParent;
				pParent = pParent->_pParent;
			} 
			else { // 父节点不平衡，需要旋转调整
				if (pParent->_bf == 2) {
					if (pCur->_bf == 1) // LL型
						// 左单旋
						RotateL(pParent);
					else // LR型
						// 先左旋后右旋
						RotateRL(pParent);
				}
				else {
					if (pCur->_bf == -1) // RR型
						// 右单旋
						RotateR(pParent);
					else // RL型
						// 先左旋后右旋
						RotateLR(pParent);
				}
				break;
			}
		}
		return true;
	}

	// AVL树的验证
	bool IsAVLTree()
	{
		return _IsAVLTree(_pRoot);
	}

private:
	// 根据AVL树的概念验证pRoot是否为有效的AVL树
	bool _IsAVLTree(Node* pRoot) {
		if (pRoot == nullptr)
			return true;

		int leftHeight = _Height(pRoot->_pLeft);
		int rightHeight = _Height(pRoot->_pRight);

		if (abs(leftHeight - rightHeight) > 1)
			return false;

		return _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight);
	}
	size_t _Height(Node* pRoot) {
		if (pRoot == nullptr)
			return 0;

		int leftHeight = _Height(pRoot->_pLeft);
		int rightHeight = _Height(pRoot->_pRight);

		return 1 + max(leftHeight, rightHeight);
	}
	// 右单旋
	void RotateR(Node* pParent) {
		Node* pSubL = pParent->_pLeft;
		Node* pSubLR = pSubL->_pRight;

		// 右旋
		pParent->_pLeft = pSubLR;
		if (pSubLR)
			pSubLR->_pParent = pParent;

		pSubL->_pRight = pParent;
		pSubL->_pParent = pParent->_pParent;
		pParent->_pParent = pSubL;

		if (pParent == _pRoot)
			_pRoot = pSubL;
		else {
			if (pSubL->_pParent->_pLeft == pParent)
				pSubL->_pParent->_pLeft = pSubL;
			else
				pSubL->_pParent->_pRight = pSubL;
		}

		pParent->_bf = pSubL->_bf = 0;
	}
	// 左单旋
	void RotateL(Node* pParent) {
		Node* pSubR = pParent->_pRight;
		Node* pSubRL = pSubR->_pLeft;

		// 左旋
		pParent->_pRight = pSubRL;
		if (pSubRL)
			pSubRL->_pParent = pParent;

		pSubR->_pLeft = pParent;
		pSubR->_pParent = pParent->_pParent;
		pParent->_pParent = pSubR;

		if (pParent == _pRoot)
			_pRoot = pSubR;
		else
		{
			if (pSubR->_pParent->_pLeft == pParent)
				pSubR->_pParent->_pLeft = pSubR;
			else
				pSubR->_pParent->_pRight = pSubR;
		}

		pParent->_bf = pSubR->_bf = 0;
	}
	// 右左双旋
	void RotateRL(Node* pParent) {
		// 先右旋后左旋
		Node* pSubR = pParent->_pRight;
		Node* pSubRL = pSubR->_pLeft;

		// 旋转之前，保存pSubRL的平衡因子，旋转完成之后，需要根据该平衡因子来调整其他节点的平衡因子
		int bf = pSubRL->_bf;

		// 进行右单旋
		RotateR(pParent->_pRight);

		//进行左单旋
		RotateL(pParent);
		if (1 == bf)
			pParent->_bf = -1;
		else if (-1 == bf)
			pSubR->_bf = 1;
	}
	// 左右双旋
	void RotateLR(Node* pParent) {
		// 先左旋后右旋
		Node* pSubL = pParent->_pLeft;
		Node* pSubLR = pSubL->_pRight;

		// 旋转之前，保存pSubLR的平衡因子，旋转完成之后，需要根据该平衡因子来调整其他节点的平衡因子
		int bf = pSubLR->_bf;

		// 进行左单旋
		RotateL(pParent->_pLeft);

		// 进行右单旋
		RotateR(pParent);
		if (1 == bf)
			pSubL->_bf = -1;
		else if (-1 == bf)
			pParent->_bf = 1;
	}

private:
	Node* _pRoot;
};

// test.cpp
#include <iostream>
#include <ctime>
#include <cstdlib>
#include "AVLTree.h"


int main() {
    AVLTree<int> avlTree;
    const int NUM_VALUES = 1000000;

    // 生成并插入 10 万个随机整数值
    srand(static_cast<unsigned int>(time(nullptr)));
    for (int i = 0; i < NUM_VALUES; ++i) {
        int randomValue = rand() % 1000000; // 生成 0 到 999999 之间的随机整数
        avlTree.Insert(randomValue);
    }

    // 验证是否为 AVL 树
    if (avlTree.IsAVLTree()) {
        std::cout << "AVL Tree validation: This is an AVL tree." << std::endl;
    }
    else {
        std::cout << "AVL Tree validation: This is not an AVL tree." << std::endl;
    }

    return 0;
}

总结

本篇博客深入介绍了AVL树，包括其原理、实现和应用。通过C++代码示例展示了AVL树的基本结构和操作，以及探讨了在计算机科学领域的广泛应用。整体内容帮助读者更好地理解和应用AVL树这一自平衡的二叉搜索树。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1523637.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Python主成分分析和聚类分析

Python主成分分析和聚类分析

项目背景 最近遇到这样一个需求&#xff1a; Python主成分分析和聚类分析&#xff1f;商业场景你数据不变展示&#xff0c;主要是用来划分用户等级&#xff0c;用来人文关怀。 基本概念 主成分分析&#xff08;PCA&#xff09;是一种常用的数据降维技术&#xff0c;通过线性变…
阅读更多...
力扣巧题：翻倍链表的元素

力扣巧题：翻倍链表的元素

此题的巧妙之处在于题目数据非常大只能在原链表中解决&#xff0c;遇到进一的问题如果尽早判断就不会有问题&#xff0c;而且第一位的判断非常巧妙 struct ListNode* doubleIt(struct ListNode* head){struct ListNode* Node (struct ListNode*)malloc(sizeof(struct ListNod…
阅读更多...
ts版本微信小程序在wxml保存文件不刷新页面的解决办法

ts版本微信小程序在wxml保存文件不刷新页面的解决办法

将project.config.json中的skylineRenderEnable改为false "skylineRenderEnable": false
阅读更多...
鸿蒙Harmony应用开发—ArkTS声明式开发（基础手势：TextClock）

鸿蒙Harmony应用开发—ArkTS声明式开发（基础手势：TextClock）

TextClock组件通过文本将当前系统时间显示在设备上。支持不同时区的时间显示&#xff0c;最高精度到秒级。 说明&#xff1a; 该组件从API Version 8开始支持。后续版本如有新增内容&#xff0c;则采用上角标单独标记该内容的起始版本。 子组件 无 接口 TextClock(options?…
阅读更多...
【数据库】基础操作

【数据库】基础操作

系列文章目录 &#x1f308;座右铭&#x1f308;&#xff1a;人的一生这么长、你凭什么用短短的几年去衡量自己的一生&#xff01; &#x1f495;个人主页:清灵白羽 漾情天殇_计算机底层原理,深度解析C,自顶向下看Java-CSDN博客 ❤️相关文章❤️&#xff1a;清灵白羽 漾情天…
阅读更多...
118. 杨辉三角（Java）

118. 杨辉三角（Java）

这里写目录标题 题目描述&#xff1a;输入:输出:代码实现&#xff1a; 题目描述&#xff1a; 给定一个非负整数 numRows&#xff0c;生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中&#xff0c;每个数是它左上方和右上方的数的和。 输入: numRows 5输出: [[1],[1,1],[1…
阅读更多...
软件功能测试内容有哪些?湖南长沙软件测评公司分享

软件功能测试内容有哪些?湖南长沙软件测评公司分享

软件功能测试主要是验证软件应用程序的功能&#xff0c;且不管功能是否根据需求规范运行。是通过给出适当的输入值&#xff0c;确定输出并使用预期输出验证实际输出来测试每个功能。也可以看作“黑盒测试”&#xff0c;因为功能测试不用考虑程序内部结构和内部特性&#xff0c;…
阅读更多...
24.第12届蓝桥杯省赛真题题解

24.第12届蓝桥杯省赛真题题解

A.空间&#xff08;100%&#xff09; 计算机存储单位计算 1TB2^10 GB 1GB2^10 MB 1MB2^10 KB 1KB2&10 B 1B8 bit(bit位二进制的最小的存储单位) #include <iostream> #include <cmath>using namespace std; //2^28B 2^2int main(){std::ios::sync_with_stdio…
阅读更多...
MySQL初阶3——事务的初步理解

MySQL初阶3——事务的初步理解

目录 一、事务的引入⭐⭐⭐⭐⭐ 1. 为什么需要事务 2. 事务的四大特性 二、事务的具体细节⭐⭐⭐⭐⭐ 1. 事务在并发会遇到的三种常见问题 2. MySQL事务隔离的四种级别 三、MySQL中如何开启事务 四、补充 很荣幸与诸君在篇文章“相遇”&#xff0c;祝大家身体健康&…
阅读更多...
UnityShader：IBL

UnityShader：IBL

效果&#xff1a; 实现&#xff1a; Shader "MyShader/IBL" {Properties{_CubeMap ("环境贴图", Cube) "white" {}_Exposure("曝光",float)1.0_Color("颜色",color)(1,1,1,1)_NormalMap("法线贴图",2d)"bu…
阅读更多...
JS仿淘宝滚动刷新简单实现

JS仿淘宝滚动刷新简单实现

废话不多说&#xff0c;直接上代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title></title><style>* {margin: 0;padding: 0;}.box {width: 24.5%;height: 200px;float: left;}.box>…
阅读更多...
#QT（事件--快捷键保存文件）

#QT（事件--快捷键保存文件）

1.IDE&#xff1a;QTCreator 2.实验&#xff1a;QEvent,QMouseEvent,QKeyEvent。 在上一个文本编辑器的基础上实现快捷键"ctrls"保存文件。 3.记录 &#xff08;1&#xff09;查看QEVENT的有效事件 &#xff08;2&#xff09; 所有时间均继承于QEvent&#xff0c;任…
阅读更多...
机试:元音处理

机试:元音处理

问题描述 代码示例 #include <bits/stdc.h> using namespace std;int main(){char string[1000];char ch getchar();int i 0;while(ch ! \n){string[i] ch;ch getchar();}char str[1000];int k 0;for(int j 0; j < i; j){if(string[j] a || string[j] e || …
阅读更多...
(含链接)2024年NVIDIA GPU技术大会开发者合集(专为开发者挑选的合集)

(含链接)2024年NVIDIA GPU技术大会开发者合集(专为开发者挑选的合集)

2024年NVIDIA GPU技术大会开发者合集 我专门为开发者整理了NVIDIA GPU技术大会上专注技术的内容合集, 希望可以帮助开发者朋友们快速了解NVIDIA的最新技术. 注意:在电脑端打开更友好, 可以直接进入每一项的网页 文章目录 2024年NVIDIA GPU技术大会开发者合集如何登录和预约会…
阅读更多...
Nacos注册中心与配置管理

Nacos注册中心与配置管理

Nacos注册中心与配置管理 1 Nacos注册中心1.1.认识Nacos1.2.服务注册到nacos1.3.服务分级存储模型1.4.权重配置1.5.环境隔离1.6.Nacos与Eureka的区别 2 CAP3.Nacos配置管理3.1.统一配置管理3.2.bootstrap了解3.3.配置热更新3.4.配置共享 1 Nacos注册中心 1.1.认识Nacos 国内公…
阅读更多...
【经验总结】ubuntu 20.04 git 上传本地文件给 github，并解决出现的问题

【经验总结】ubuntu 20.04 git 上传本地文件给 github，并解决出现的问题

1. 在GitHub 上创建仓库 登录 GitHub 个人网站 点击 New 填写 Repository name, 以及 Description (optional) 选择 Public &#xff0c; 并添加 Add a README file 点击 Create repository github repository 创建成功 2. 设置SSH key 在本地 bash 运行&#xff1a;…
阅读更多...
Android Kotlin（五）数据流StateFlow和LiveData

Android Kotlin（五）数据流StateFlow和LiveData

Android 上的 Kotlin 数据流 在协程中&#xff0c;与仅返回单个值的挂起函数相反&#xff0c;数据流可按顺序发出多个值。数据流以协程为基础构建&#xff0c;可提供多个值。从概念上来讲&#xff0c;数据流是可通过异步方式进行计算处理的一组数据序列。所发出值的类型必须…
阅读更多...
小迪安全42WEB攻防-通用漏洞文件包含LFIRFI伪协议

小迪安全42WEB攻防-通用漏洞文件包含LFIRFI伪协议

#知识点: 1、解释什么是文件包含 2、分类-本地LFI&远程RFI 3、利用-配合上传&日志&会话 4、利用-伪协议&编码&算法等 #核心知识: 1、本地包含LFI&远程包含RF1-区别 一个只能包含本地&#xff0c;一个可以远程加载 具体形成原因由代码和环境配置文件决定…
阅读更多...
PyQt5使用

PyQt5使用

安装Pyqt5信号与槽使用可视化界面编辑UI (Pyside2)ui生成之后的使用(两种方法)1 ui转化为py文件 进行import2 动态调用UI文件 安装Pyqt5 pip install pyqt5-tools这时候我们使用纯代码实现一个简单的界面 from PyQt5.QtWidgets import QApplication, QMainWindow, QPushButto…
阅读更多...
练习8 Web [GYCTF2020]Blacklist

练习8 Web [GYCTF2020]Blacklist

这道题其实不是堆叠注入&#xff0c;但是我在联合查询无效后&#xff0c;试了一下堆叠&#xff0c;最后一步发现被过滤的sql语句太多了&#xff0c;完全没法 查阅其他wp的过程[GYCTF2020]Blacklist 1&#xff08;详细做题过程&#xff09; 是用的handler语句&#xff0c;只能用…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023