文章目录
- 🧡🧡t1_奇数次数🧡🧡
- 思路
- 代码
- 🧡🧡t2_台阶方案🧡🧡
- 思路
- 代码
- 🧡🧡t3_约数个数🧡🧡
- 思路
- 代码
- 🧡🧡t4_最大子矩阵🧡🧡
- 思路
- 代码
- 🧡🧡t5_最少步数🧡🧡
- 思路
- 代码
- 🧡🧡t6_最大极小值与最小极大值🧡🧡
- 思路
- 代码
- 🧡🧡t7_最大的Y🧡🧡
- 思路
- 代码
- 🧡🧡t8_左右相同🧡🧡
- 思路
- 代码
- 🧡🧡t9_求余数🧡🧡
- 思路
- 代码
- 🧡🧡t10_区间计数🧡🧡
- 思路
- 代码
- 🧡🧡t11_数位和🧡🧡
- 思路
- 代码
前两期题目解析👇
15届蓝桥杯第一期模拟赛题单详细解析
15届蓝桥杯第二期模拟赛题单详细解析
🧡🧡t1_奇数次数🧡🧡


思路
遍历判断即可,简单。
代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
String string = sc.next();
int cnt = 0;
for (char c : string.toCharArray()) {
if ((int) (c - '0') % 2 == 1)
cnt++;
}
System.out.println(cnt);
}
}
🧡🧡t2_台阶方案🧡🧡


思路
一开始想着直接dfs深搜,但试了下n=1000的情况,跑了很久都没结果,估计了一下时间复杂度为 3 0 + 3 1 + . . . . . . 3 1000 3^0+3^1+......3^{1000} 30+31+......31000。因此小一点的n还可以直接搜出答案,但是过大就不行。
尝试找规律:可以发现,若走台阶方法为a=1,b=2,c=3的情况下,n取1到10,分别为:
可以发现(用f[i]表示对于n=i的方案数):
- f [4] = f [1] +f [2] +f [3]
- f [5] = f [2] +f [3] +f [4]
- f [6] = f [3] +f [4] +f [5]
- 因此可以归纳出:f【n】=f【n-1】+f【n-2】+f【n-3】。代表什么含义呢?拿f [6]解释,可以理解为:
在a=1,b=2,c=3三种跨台阶阶级的情况下,n=6可以
- 从n=5走a=1阶到达,即在n=5的情况下,再走1次 a=1阶就能到达n=6
- 从n=4走b=2阶到达,即在n=4的情况下,再走1次b=2阶就能到达n=6
- 从n=3走c=3阶到达,即在n=3的情况下,再走1次 c=3阶就能到达n=6
从而, 更一般地归纳为:f【n】=f【n-a】+f【n-b】+f【n-c】,因此只要逐个递推出f【n】即可。
需要额外规定的是,f【0】=1。
代码
import java.util.Scanner;
public class Main {
public static int a, b, c;
public static int[] f = new int[1000010];
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
a = scanner.nextInt();
b = scanner.nextInt();
c = scanner.nextInt();
f[0] = 1;
for (int i = 1; i <= n; i++) {
if (i - a >= 0)
f[i] = (f[i] + f[i - a]) % 1000000007;
if (i - b >= 0)
f[i] = (f[i] + f[i - b]) % 1000000007;
if (i - c >= 0)
f[i] = (f[i] + f[i - c]) % 1000000007;
}
System.out.println(f[n] % 1000000007);
}
}
🧡🧡t3_约数个数🧡🧡

思路
枚举
代码
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
int cnt = 0;
for (int i = 1; i <= 2023; i++) {
if (2023 % i == 0)
cnt++;
}
System.out.println(cnt);
}
}
🧡🧡t4_最大子矩阵🧡🧡
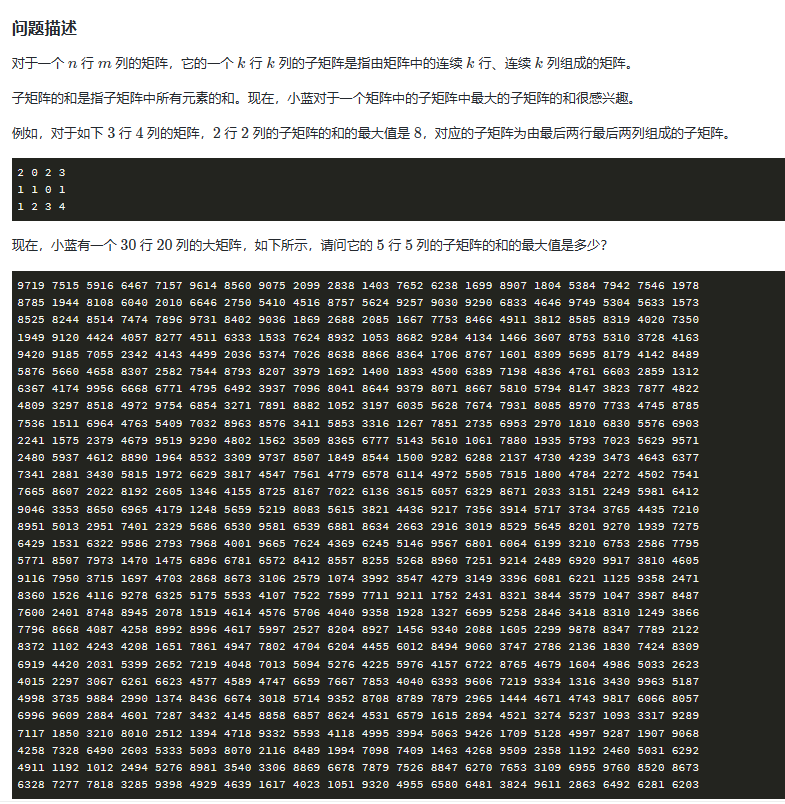
9719 7515 5916 6467 7157 9614 8560 9075 2099 2838 1403 7652 6238 1699 8907 1804 5384 7942 7546 1978
8785 1944 8108 6040 2010 6646 2750 5410 4516 8757 5624 9257 9030 9290 6833 4646 9749 5304 5633 1573
8525 8244 8514 7474 7896 9731 8402 9036 1869 2688 2085 1667 7753 8466 4911 3812 8585 8319 4020 7350
1949 9120 4424 4057 8277 4511 6333 1533 7624 8932 1053 8682 9284 4134 1466 3607 8753 5310 3728 4163
9420 9185 7055 2342 4143 4499 2036 5374 7026 8638 8866 8364 1706 8767 1601 8309 5695 8179 4142 8489
5876 5660 4658 8307 2582 7544 8793 8207 3979 1692 1400 1893 4500 6389 7198 4836 4761 6603 2859 1312
6367 4174 9956 6668 6771 4795 6492 3937 7096 8041 8644 9379 8071 8667 5810 5794 8147 3823 7877 4822
4809 3297 8518 4972 9754 6854 3271 7891 8882 1052 3197 6035 5628 7674 7931 8085 8970 7733 4745 8785
7536 1511 6964 4763 5409 7032 8963 8576 3411 5853 3316 1267 7851 2735 6953 2970 1810 6830 5576 6903
2241 1575 2379 4679 9519 9290 4802 1562 3509 8365 6777 5143 5610 1061 7880 1935 5793 7023 5629 9571
2480 5937 4612 8890 1964 8532 3309 9737 8507 1849 8544 1500 9282 6288 2137 4730 4239 3473 4643 6377
7341 2881 3430 5815 1972 6629 3817 4547 7561 4779 6578 6114 4972 5505 7515 1800 4784 2272 4502 7541
7665 8607 2022 8192 2605 1346 4155 8725 8167 7022 6136 3615 6057 6329 8671 2033 3151 2249 5981 6412
9046 3353 8650 6965 4179 1248 5659 5219 8083 5615 3821 4436 9217 7356 3914 5717 3734 3765 4435 7210
8951 5013 2951 7401 2329 5686 6530 9581 6539 6881 8634 2663 2916 3019 8529 5645 8201 9270 1939 7275
6429 1531 6322 9586 2793 7968 4001 9665 7624 4369 6245 5146 9567 6801 6064 6199 3210 6753 2586 7795
5771 8507 7973 1470 1475 6896 6781 6572 8412 8557 8255 5268 8960 7251 9214 2489 6920 9917 3810 4605
9116 7950 3715 1697 4703 2868 8673 3106 2579 1074 3992 3547 4279 3149 3396 6081 6221 1125 9358 2471
8360 1526 4116 9278 6325 5175 5533 4107 7522 7599 7711 9211 1752 2431 8321 3844 3579 1047 3987 8487
7600 2401 8748 8945 2078 1519 4614 4576 5706 4040 9358 1928 1327 6699 5258 2846 3418 8310 1249 3866
7796 8668 4087 4258 8992 8996 4617 5997 2527 8204 8927 1456 9340 2088 1605 2299 9878 8347 7789 2122
8372 1102 4243 4208 1651 7861 4947 7802 4704 6204 4455 6012 8494 9060 3747 2786 2136 1830 7424 8309
6919 4420 2031 5399 2652 7219 4048 7013 5094 5276 4225 5976 4157 6722 8765 4679 1604 4986 5033 2623
4015 2297 3067 6261 6623 4577 4589 4747 6659 7667 7853 4040 6393 9606 7219 9334 1316 3430 9963 5187
4998 3735 9884 2990 1374 8436 6674 3018 5714 9352 8708 8789 7879 2965 1444 4671 4743 9817 6066 8057
6996 9609 2884 4601 7287 3432 4145 8858 6857 8624 4531 6579 1615 2894 4521 3274 5237 1093 3317 9289
7117 1850 3210 8010 2512 1394 4718 9332 5593 4118 4995 3994 5063 9426 1709 5128 4997 9287 1907 9068
4258 7328 6490 2603 5333 5093 8070 2116 8489 1994 7098 7409 1463 4268 9509 2358 1192 2460 5031 6292
4911 1192 1012 2494 5276 8981 3540 3306 8869 6678 7879 7526 8847 6270 7653 3109 6955 9760 8520 8673
6328 7277 7818 3285 9398 4929 4639 1617 4023 1051 9320 4955 6580 6481 3824 9611 2863 6492 6281 6203
思路
方法1:最简单的,由于是填空题,且数据大小只有30×20,可以直接模拟一个5×5的小正方形,依次计算最值即可。(类似CNN卷积核提取特征)
方法2:可对方法1进行时间优化,利用前缀和思想。
代码
import java.util.Scanner;
public class t4_最大子矩阵 {
public static int[][] grid = new int[35][25];
public static int[][] s = new int[35][25];
public static void main(String[] args) {
// TODO Auto-generated method stub
// Scanner scanner = new Scanner(System.in);
// int n = 30;
// int m = 20;
// int k = 5;
// for (int i = 1; i <= n; i++) {
// for (int j = 1; j <= m; j++) {
// grid[i][j] = scanner.nextInt();
// }
// }
// for (int i = 1; i <= n; i++) {
// for (int j = 1; j <= m; j++) {
// s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + grid[i][j];
// }
// }
// int maxv = Integer.MIN_VALUE;
// for (int i = 1; i <= n - 5 + 1; i++) {
// for (int j = 1; j <= m - 5 + 1; j++) {
// int tmp = s[i + k - 1][j + k - 1] - s[i + k - 1][j - 1] - s[i - 1][j + k - 1] + s[i - 1][j - 1];
// maxv = Math.max(maxv, tmp);
// }
// }
// System.out.println(maxv);
System.out.println(171248);
}
}
🧡🧡t5_最少步数🧡🧡

思路
咋一看跟t2_台阶方案好像,实则就是数学问题。要求最小步数,保证每一步尽量跨最大一步(3)即可,直到剩下的台阶用1或2补足就好了。
代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int ans = 0;
if (n % 3 == 0)
ans = n / 3;
else
ans = n / 3 + 1;
System.out.println(ans);
}
}
🧡🧡t6_最大极小值与最小极大值🧡🧡

思路
枚举
代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] arr = new int[n + 1];
for (int i = 1; i <= n; i++) {
arr[i] = scanner.nextInt();
}
int minv = Integer.MAX_VALUE;
int maxv = Integer.MIN_VALUE;
for (int i = 1; i <= n - 1; i++) {
if (arr[i] < arr[i - 1] && arr[i] < arr[i + 1])
maxv = Math.max(maxv, arr[i]);
if (arr[i] > arr[i - 1] && arr[i] > arr[i + 1])
minv = Math.min(minv, arr[i]);
}
System.out.println(maxv + " " + minv);
}
}
🧡🧡t7_最大的Y🧡🧡

7 7
1000001
0100010
0010100
0001AAA
00010A0
00010A0
00010A0
3
思路
遍历每个坐标点,依次在该点上模拟三个方向,计算三个方向各自所能到达的距离,取它们的最小值,即为该点的“Y的长度”。最后,取所有点的“Y的长度”的最大值即为答案。
代码
import java.util.Scanner;
public class Main {
public static char[][] grid = new char[1005][1005];
public static int n, m;
public static int check(int x, int y, char ch) {
// 左上45度
int tx = x - 1;
int ty = y - 1;
int cnt1 = 0;
while (tx >= 1 && tx <= n && ty >= 1 && ty <= m && grid[tx][ty] == ch) {
cnt1++;
tx--;
ty--;
}
// System.out.println(tx + " " + ty);
// 右上45度
tx = x - 1;
ty = y + 1;
int cnt2 = 0;
while (tx >= 1 && tx <= n && ty >= 1 && ty <= m && grid[tx][ty] == ch) {
cnt2++;
tx--;
ty++;
}
// 正下4
tx = x + 1;
ty = y;
int cnt3 = 0;
while (tx >= 1 && tx <= n && ty >= 1 && ty <= m && grid[tx][ty] == ch) {
cnt3++;
tx++;
}
return Math.min(Math.min(cnt1, cnt2), cnt3);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
for (int i = 1; i <= n; i++) {
String str = scanner.next();
for (int j = 1; j <= m; j++) {
grid[i][j] = str.charAt(j - 1);
}
}
int ans = Integer.MIN_VALUE;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
ans = Math.max(ans, check(i, j, grid[i][j]));
}
}
System.out.println(ans);
}
}
🧡🧡t8_左右相同🧡🧡

思路
枚举模拟
代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
String s = sc.next();
int ans = 0;
int cnt1 = 0;
int cnt2 = 0;
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if (ch == 'L')
cnt1++;
else
cnt2++;
if (cnt1 == cnt2)
ans++;
}
System.out.println(ans);
}
}
🧡🧡t9_求余数🧡🧡

思路
跟第二期模拟赛的第1道题差不多,也是大数问题,这里直接采用BigInteger来处理了。
代码
import java.math.BigInteger;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
BigInteger n1 = new BigInteger("12345678901234567890123456789012345678901234567890");
BigInteger n2 = new BigInteger("2023");
BigInteger res = n1.mod(n2);
System.out.println(res.toString());
}
}
🧡🧡t10_区间计数🧡🧡

思路
枚举
代码
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
int ans = 0;
for (int l = 0; l <= 100; l++) {
for (int r = l; r <= 100; r++) {
if (r - l >= 10)
ans++;
}
}
System.out.println(ans);
}
}
🧡🧡t11_数位和🧡🧡

思路
枚举模拟
代码
public class Main {
public static boolean isPrime(int n) {
if (n <= 1)
return false;
if (n == 2)
return true;
for (int i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0)
return false;
}
return true;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
int ans = 0;
for (int i = 1; i <= 1000000; i++) {
if (isPrime(i)) {
int x = i;
int tmp = 0;
while (x > 0) {
tmp += x % 10;
x /= 10;
}
if (tmp == 23)
ans++;
}
}
System.out.println(ans);
}
}