算法题
Leetcode 235. 二叉搜索树的最近公共祖先
题目链接:235. 二叉搜索树的最近公共祖先
大佬视频讲解:二叉搜索树的最近公共祖先视频讲解
个人思路
昨天做过一道二叉树的最近公共祖先,而这道是二叉搜索树,那就要好好利用这个有序的特点来解决这道题,因为是有序树,所以如果 中间节点是 q 和 p 的公共祖先,那么 中节点的数组 一定是在 [p, q]区间的。即 中节点 > p && 中节点 < q 或者 中节点 > q && 中节点 < p。
解法
递归法
那么只要从上到下去遍历,遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是p 和 q的公共祖先。但一定是最近公共祖先吗?画个图看看
如图下,从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点7,此时可以说明 q 和 p 一定分别存在于 节点 7的左子树,和右子树中。
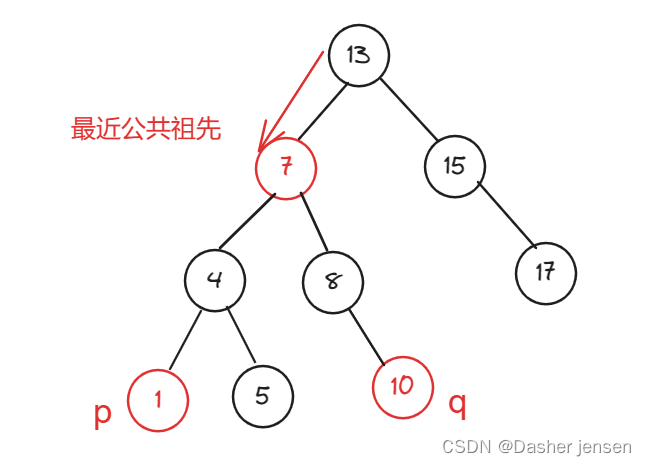
所以从上向下去递归遍历,第一次遇到 cur节点是数值在[q, p]区间中,那么cur就是 q和p的最近公共祖先.
这道题和二叉树的搜索还有一点不同,就是本题就是标准的搜索一条边的写法,遇到递归函数的返回值,如果不为空,立刻返回。
再加上这道题没有递归顺序,因为这里没有中节点的处理逻辑;递归函数就很简单了如下
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val > p.val && root.val > q.val) //终止条件
{return lowestCommonAncestor(root.left, p, q);}//递归过程
if (root.val < p.val && root.val < q.val)
{return lowestCommonAncestor(root.right, p, q);}
return root;//返回参数
}
}时间复杂度:O(n);(遍历整棵树)
空间复杂度:O(n);(递归树的高度,如果是一个高度不平衡的树(例如链状结构)高度与n接近)
迭代法
和递归法思路相似,改成了while循环,找到最近公共祖先就返回节点;
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while (true) {
//遍历选择方向
if (root.val > p.val && root.val > q.val) {//若大了,就往小的方向靠即树的左边
root = root.left;
} else if (root.val < p.val && root.val < q.val) {
root = root.right;
} else {
break;
}
}
return root;
}
}时间复杂度:O(n);(遍历整棵树)
空间复杂度:O(1);(只有一个节点)
Leetcode 701.二叉搜索树中的插入操作
题目链接:701.二叉搜索树中的插入操作
大佬视频讲解:二叉搜索树中的插入操作视频讲解
个人思路
因为说还可以重构二叉树,一时间不知道怎么下手
解法
递归法
可以不考虑题目中提示所说的改变树的结构的插入方式,只考虑如何插入节点,只要按照二叉搜索树的规则去遍历,遇到空节点就插入节点就可以了。
递归三步走:
1.确定递归函数参数以及返回值
参数就是根节点指针,以及要插入元素,
递归函数需要有返回值,可以利用返回值完成新加入的节点与其父节点的赋值操作。
递归函数的返回类型为节点类型TreeNode * 。
2.确定终止条件
终止条件就是找到遍历的节点为null的时候,就是要插入节点的位置了,并把插入的节点返回。
3.确定单层递归的逻辑
搜索树是有方向了,可以根据插入元素的数值,决定递归方向。
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
// 如果当前节点为空,也就意味着val找到了合适的位置,此时创建节点直接返回。
if (root == null) { return new TreeNode(val);}
if (root.val < val){
root.right = insertIntoBST(root.right, val); // 递归创建右子树
}else if (root.val > val){
root.left = insertIntoBST(root.left, val); // 递归创建左子树
}
return root;
}
}时间复杂度:O(n);(最差遍历一遍树)
空间复杂度:O(n);(递归树的高度,如果是一个高度不平衡的树(例如链状结构)高度与n接近)
迭代法
迭代的方法就需要记录当前遍历节点的父节点了,这个和没有返回值的递归函数实现的代码逻辑是一样的。
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) return new TreeNode(val);
TreeNode newRoot = root;
TreeNode pre = root;//父节点
while (root != null) {
pre = root;
if (root.val > val) {//利用二叉树特点
root = root.left;
} else if (root.val < val) {
root = root.right;
}
}
//当root为空时,就找到了插入节点的位置,再根据值的大小选择插入左边还是右边
if (pre.val > val) {
pre.left = new TreeNode(val);
} else {
pre.right = new TreeNode(val);
}
return newRoot;
}
}时间复杂度:O(n);(遍历整棵树)
空间复杂度:O(1);(因为是原地修改树的方式进行插入,不涉及递归调用栈的空间增长;除了返回的新节点外,算法不需要额外的空间来存储任何信息)
Leetcode 450.删除二叉搜索树中的节点
题目链接:450.删除二叉搜索树中的节点
大佬视频讲解:删除二叉搜索树中的节点视频讲解
个人思路
思路不清晰,主要是如何在删除节点后有多少种情况要解决不太明白
解法
递归法
因为二叉搜索树添加节点只需要在叶子上添加就可以的,不涉及到结构的调整,而删除节点操作涉及到结构的调整。这里使用递归函数的返回值来完成把节点从二叉树中移除的操作。
递归三步走:
1.确定递归函数参数以及返回值
上道题是通过递归返回值来加入新节点, 这里也可以通过递归返回值删除节点。
2.确定终止条件
遇到空返回,其实这也说明没找到删除的节点,遍历到空节点直接返回了
3.确定单层递归的逻辑
二叉搜索树中删除节点遇到的情况有以下五种情况:
- 第一种情况:没找到删除的节点,遍历到空节点直接返回了
- 找到删除的节点
- 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
- 第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
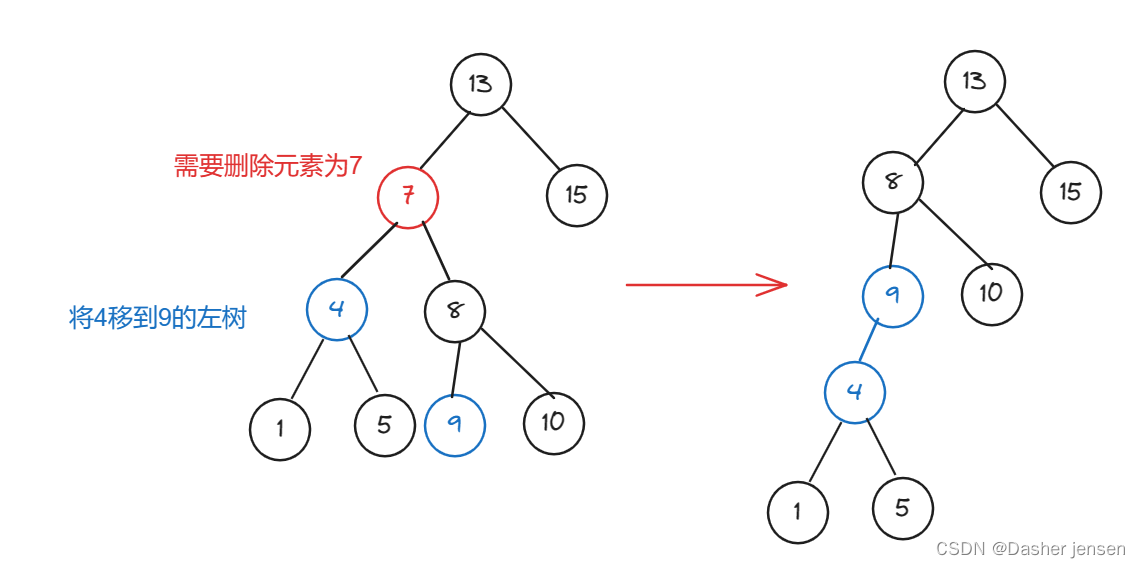
- 第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
其中第五种情况比较难理解,画图理解,如下。
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return root;//终止条件
if (root.val == key) {//找到删除节点
if (root.left == null) {
return root.right;
} else if (root.right == null) {
return root.left;
} else {
TreeNode cur = root.right;
while (cur.left != null) {
cur = cur.left;
}
cur.left = root.left;//左右孩子都不为空的情况
root = root.right;
return root;
}
}
if (root.val > key) root.left = deleteNode(root.left, key);//遍历左树
if (root.val < key) root.right = deleteNode(root.right, key);
return root;
}
}时间复杂度:O(n);(遍历二叉树)
空间复杂度:O(n);(递归树的高度,如果是一个高度不平衡的树(例如链状结构)高度与n接近)
迭代法
用迭代法模拟递归法中的逻辑来删除节点,但需要一个pre记录cur的父节点,方便做删除操作。
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null){
return null;
}
//寻找对应的对应的前面的节点,以及他的前一个节点
TreeNode cur = root;
TreeNode pre = null;//父节点
while (cur != null){
if (cur.val < key){
pre = cur;
cur = cur.right;
} else if (cur.val > key) {
pre = cur;
cur = cur.left;
}else {
break;
}
}
if (pre == null){
return deleteOneNode(cur);
}
if (pre.left !=null && pre.left.val == key){
pre.left = deleteOneNode(cur);
}
if (pre.right !=null && pre.right.val == key){
pre.right = deleteOneNode(cur);
}
return root;
}
public TreeNode deleteOneNode(TreeNode node){//处理删除节点的情况
if (node == null){
return null;
}
if (node.right == null){
return node.left;
}
TreeNode cur = node.right;
while (cur.left !=null){
cur = cur.left;
}
cur.left = node.left;
return node.right;
}
}时间复杂度:O(n);(遍历二叉树)
空间复杂度:O(1);(因为是原地修改树的方式进行插入,不涉及递归调用栈的空间增长;除了返回的新节点外,算法不需要额外的空间来存储任何信息)
以上是个人的思考反思与总结,若只想根据系列题刷,参考卡哥的网址代码随想录算法官网