前言：

这道题原本是蓝桥上的题，现在搜不到了，网上关于此题的讲解更是寥寥无几，仅有的讲解也只是递归思想，python讲解和状态压缩dp的解决方法都没有，这里就带大家用状态压缩dp方法来解决此题。

题目：

大奖赛计分规则：
每位选手需要回答10个问题（其编号为1到10），越后面越有难度。答对的，当前分数翻倍；答错了，则扣掉与题号相同的分数（选手必须回答问题，不回答按错误处理）。每位选手的起步分都是10分，某获胜选手最终得分刚好是100分，请推断出哪个题目答对了，哪个题目答错了？（答对的记为1，答错的记为0，则10个题目的回答情况可用仅含1和0的串来表示）。任务是算出所有可能情况，每个答案占一行。（填空题）

输出：
0010110011
0111010000
1011010000

思路：

递归：

分析本题首先想到递归思想，从得分100逆推出初始分数为10的方案。
首先定义一个字符串

如果本题答对了，则总得分除2，字符串首位加1（因为是从第10题往前推，所以要逆序加）

如果本题答错了，则总得分加上本题的序号数，字符串首位加0

这里还有一个小细节，如果得分是奇数，则不能除2（只能答错）。

代码及详细注释：

def ScoreOut(qs, score, out):
    # 如果qs为0
    if qs == 0:
        # 如果score等于10
        if score == 10:
            print(out)  # 输出当前字符串out
            return out  # 返回当前字符串out
        else:
            return ""  # 返回空字符串

    else:
        # 如果score为偶数
        if score % 2 == 0:
            # 递归调用函数，分别将score除以2并在开头添加字符"1"，以及将score加上qs并在开头添加字符"O"
            return ScoreOut(qs - 1, score // 2, "1" + out) + ScoreOut(qs - 1, score + qs, "O" + out)
        else:
            # 如果score为奇数，只递归调用将score加上qs并在开头添加字符"O"
            return ScoreOut(qs - 1, score + qs, "O" + out)

# 初始调用函数
ScoreOut(10, 100, "")

状态压缩dp：

什么是状态压缩：

利用一串0/1数字（二进制数）来表示各个点的状态，

这就要求使用状态压缩的对象的状态必须只有两种，0 或 1（如果有三种状态用三进制来表示也未尝不可）。

需要将状态数据实现为基本数据类型，比如 int，long 等，即状态压缩。比如说棋盘上的格子，放棋子或者不放；硬币的正面或反面；题目的对或错等。

状态压缩要求状态数据中的单元个数不能太大，比如用 int 来表示一个状态的时候，状态的单元个数不能超过 32（32位CPU），所以题目一般都是至少有一维的数据范围很小。

当然Python不需要考虑数的大小是否受限。

分析本题，上面用递归讲解过本题，有递归就用动态规划来解决，众所周知，递归很好理解和书写，但是递归的时间复杂度都不低，会有大量冗余计算。像本题中

如图：

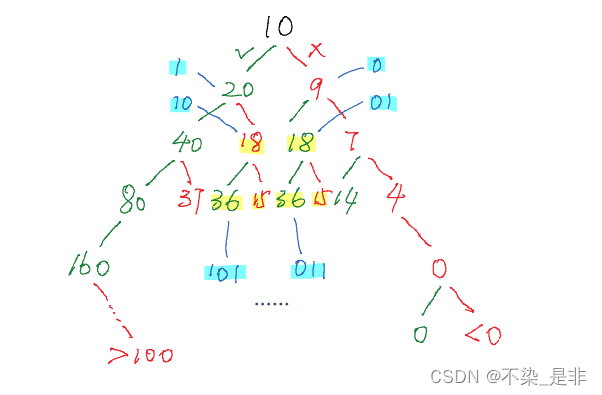
会出现大量相同得分情况，这就需要借助动态规划来处理重复计算了。

动态规划五部曲来分析：

1. 确定dp数组的定义：

对于数组dp[i] :

下标表示10道题目的对错状态，dp[i]表示对应得分

下标 i 的二进制数表示对错状态，如 i = 2 时 i 的二进制数为 10 ，此时10（第1题答错，之后的提还没有做）（二进制数）的得分为多少，i = 7 时，i的二进制数为111，此时（第1题答对，第2题答对，之后的题还没有做）的得分为多少
特别注意！！！ 这里首位的1（二进制后的数）没有实际含义，不表示题目对错，这个在下面会讲解

题目中有10道题，总共的有2 ** 10 - 1 种可能种情况（可能的情况用2进制计算就可以得出，如从000000000到111111111的可能数）

对于0000000000（这些都是10个数，不用挨个数了），二进制是这么表示，但10进制中，这个数就是0，

要想这个二进制数有意义，最前面就要加个1，否则无论有几个0，都表示0这个数，所以我们在定义dp数组长度的时候，不能为2 ** 10 而是为 2 ** 11（因为二进制1000000000（1后面10个0）的10进制数为 2 ** 11）

大家之前做题接触的二进制情况肯定不多，所以这里会稍微有点绕。这里主要理解前面自定义的1就好，跟补码的符号位有异曲同工之妙，只不过这里仅仅用来补位。

2. dp数组的递推公式：

状态压缩dp的递推公式还跟别的动规的递推公式不太一样，这里需要用到位运算符

这里简单讲解一下位运算符：

<< : 表示运算数的各二进制位全部左移若干位，低位补0
如 7 << 1 = 14， 因为7的二进制数为111，左移一位后为1110，1110的十进制数为14

右移跟左移同理。

还有python的二进制数可以用bin()函数来求，如bin(7) = 0b111，0b表示二进制，bin(7)的类型为字符串型。但是直接写0b111 就表示整型。

因为第二道题的得分是由第一道题的得分算出来的，如

dp[0b1 << 1] = dp[0b1] - 1          #   dp[0b10]即dp[2]
dp[(0b1 << 1) +1] = dp[0b1] * 2      #  dp[0b11]即dp[3]

对于第cur道题，

如果答错：dp[i << 1] = dp[i] - cur
如果答对：dp[(i << 1) + 1] = dp[i] * 2

在推导递推公式的时候如果不太清楚，就看看dp数组的定义，切记第一个1无实义

3. dp数组如何初始化：

因为第一个1无实义，所以

dp[0b1] = 10  # dp[1]初始化得分为10

4. dp数组遍历顺序：

毫无疑问，题是从前往后答的，dp数组也是从左往右推

5. 打印dp数组：

画的有点丑，下标最好写成二进制形式。

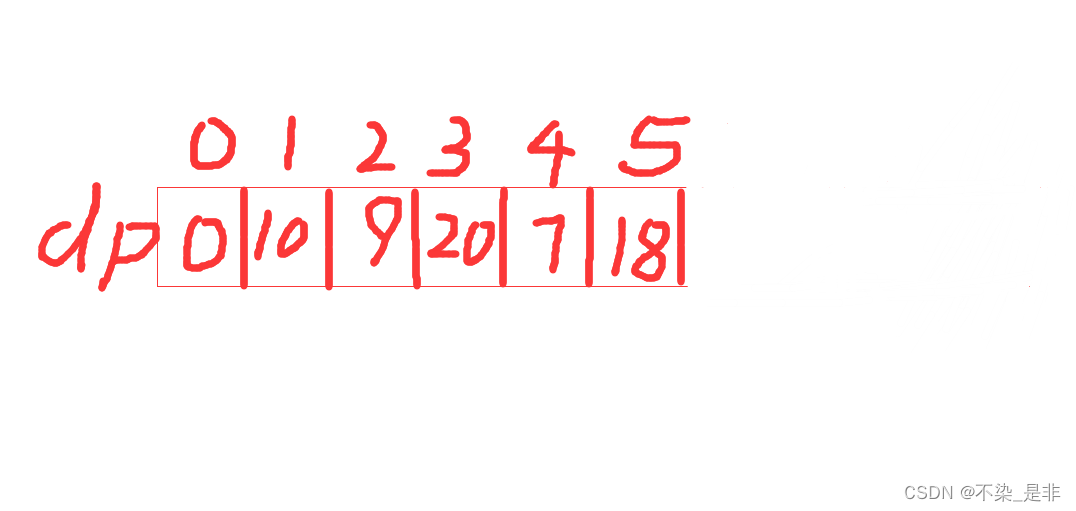
求出dp数组后就把得分为100且10道题全都做了的结果输出就行。比较简单，有很多种方法，就不细说了。

代码及详细注释：

import math

# 初始化一个长度为2^11的数组，初始值为0
dp = [0] * 2 ** 11
dp[1] = 10  # dp[1]初始化得分为10
# dp[0b1 <<1] = dp[0b1] - 1             dp[0b10]即dp[2]
# dp[(0b1 <<1) +1] = dp[0b1] * 2        dp[0b11]即dp[3]

maxscore = 160  # 最大分数为160（因为160怎么减题目序号都到不了100，也可以设170等等）
for i in range(1, 2 ** 10):
    if dp[i] == -1:
        continue
    else:
        cur = int(math.log2(i << 1))  # 计算准备做的题目序号，因为第一个1无实际意义，1之后的数才表示题的对错
        if dp[i] - cur <= 0:
            dp[i << 1] = -1
        else:
            dp[i << 1] = dp[i] - cur
        if dp[i] * 2 >= maxscore:
            dp[(i << 1) + 1] = -1
        else:
            dp[(i << 1) + 1] = dp[i] * 2

result = []
while True:
    if 100 in dp:
        index = dp.index(100)  # 找到值为100的索引
        dp[index] = 0
        if len(bin(index)) == 13:
            result.append(bin(index))  # 将长度为13(10道题都做完了，头三位为0b1)的二进制数添加到结果列表中
    else:
        break

for res in result:
    print(res[3:])  # 输出结果列表中每个元素的第3位之后的内容

总结：

状态压缩dp还是比较难的，但把dp的定义吃透就比较好理解了。