stackBlur介绍

        stackBlur 最近才加入到OpenCV中，将在下一个Relase版本（4.7）中出现。C++用户可以尝试从源码编译OpenCV体验一下。Python 用户可以尝试用pip安装rolling版本的OpenCV：

pip install opencv-python-rolling==4.6.0.20221015

stackBlur是高斯模糊的近似，同样支持水平和垂直不对称的滤波。

stackAPI

C++API

Mat img_src, img_dst;
Size kernel_size(13, 9);
stackBlur(img_src, img_dst, kernel_size);

Python API

img_dst = cv2.stackBlur(img_src, (13, 9))

为什么StackBlur的API中s小写？OpenCV中对API有严格控制，以作者名称开头的API可以大写（如Sobel、GaussianBlur），除此之外都小写字母开头。

直接上stackBlur的使用建议和最后的实验结果：

建议当kernel size > 11时，用stackBlur替换高斯模糊；当kernel size特别大时，OpenCV的所有模糊滤波器中只推荐stackBlur。

实验结果如下：

测试环境：Mac M1，8核，image size [1920 x 2048], 数据类型：CV_8U3C。

测试方法：跑一千次，选取最小作为耗时，测试脚本在这里。

结论：stackBlur不会随着kernel size增加而增加耗时。

 原理介绍

如果你想知道关于加速的更多细节，请看下面的完整版（1万字预警）：

Stackblur的坑是2021年初老瓦给我挖的。当时我找他，说我想从事OpenCV开发，有啥事情可以干的吗？老瓦说可以尝试增加一个新滤波器stackblur。当时做了有半个月，终于把代码在OpenCV上调通并且能产生正确模糊的结果，但是卡在了速度优化上。最近在优化OpenCV的DNN模块，也学会了一些并行加速的技巧又花了两周时间终于把坑填上了。

本文介绍最近新加入OpenCV的模糊算法Stackblur，Stackblur是一种高斯模糊的快速近似，由Mario Klingemann发明。其计算耗时不会随着kernel size增大而增加，专为大kernel size的模糊滤波场景量身定制。本文从新加入OpenCV的cv::stackBlurAPI开始引入，首先介绍Stackblur和常用的高斯模糊及盒子模糊(Boxblur)的区别，然后，介绍如何将StackBlur加速到极致，最后是一些性能测试及结果分析。

如果你也想让你的滤波器跑的像OpenCV里的滤波器一样快，本文也许能给你一些启发。

大佬请直接上眼PR

滤波计算

具体计算其实和DNN的卷机层类似，这里盗用一下卷机计算过程做展示，其中左侧是原图像，中间是kernel，右侧是输出：

滤波核

不同模糊滤波算法之前区别就在于滤波核的不同，下面是kernel size为3x3对应的值。

三种滤波器在kernel size为3x3时的滤波核

可以发现，3x3情况下，高斯滤波核和Stackblur的值是一样的，这是为什么呢？

如果想知道高斯滤波核怎么产生，请参考：Jargon：OpenCV 学习：8 高斯滤波GaussianBlur

读完下节将告诉你为什么StackBlur 3x3滤波核是这个样子。在此之前，我们先了解一下一个重要的问题：对比BoxBlur和高斯模糊，Stackblur有什么优势？

首先，我们仔细研究一下BoxBlur有哪些不足，下图展示了boxblur从小kernel到大kernel的图像模糊滤波结果，可以发现，当Radius=20时（这里radius和kernel size的换算：kernel size = 2 * radius + 1），可以明显感觉输出图像有方格感。

 

再来看看高斯模糊。下图是高斯的核函数的三维图像。中心高，四周低，每个输出的像素点受到滤波核中心值的影响要比四周的影响大，这能保证高斯模糊不会像Boxblur一样出现方格感。在大kernel size情况下，高斯模糊输出的图像质量没问题。但是高斯模糊算法最大的问题在于速度，高斯模糊的耗时会随着kernel size的增大而增大，对于StackBlur和BoxBlur，其并不会随着kernel size增大而耗时增加。这是为什么？见加速部分。

高斯核函数

StackBlur算法

这里直接引入StakBlur算法的原始论文，作者只用了一页纸就说明白了。论文里仅描述了1维的StackBlur算法，2维情况是分别在水平和垂直方向做1维Stackblur即可。

包浆图片来源：https://underdestruction.com/wordpress/wp-content/uploads/2016/02/StackBlur01.png

这一页纸中，从上到下，作者将StackBlur算法从初始状态到像素计算过程展示的很清楚了。其中展示的是kernel size大小为5，或者radius = 2的1维stackblur计算过程(kernel size = radius * 2 + 1)。和之前滤波核的计算不同，这里是用Queue和Stack来计算。其中，Queue的长度等于(kernel size/2 +1)*2。不同kernel size对应的Stack形状如下图所示，后续以此类推：

不同kernel size的Stackblur中Stack所对应的形状

一旦kernel size确定之后，stack的形状也就确定了。

其中Queue分为前后两个部分，为了方便理解，我将Queue前后切开分别叫做StackOut和StackIn。

Step0: 初始状态。填充第一个像素值到StackOut、StackIn和Stack中。
Step1: 计算输出像素值。val = Sum(Stack)/Stack_NUM.
Step2: 更新StackOut、StackIn和Stack，更新方法如下：
       Stack = Stack - StackOut + StackIn；
       StackIn和StackOut向右移动一格，类似于滑动窗口。
Step3: 重复Step1，直到一行结束。

其中，Stack_NUM是由Stack中方块的数量确定，如kernel size为5时，Stack_NUM为1 + 3 + 5 = 9。

这里举个例子：当Stackblur kernel size = 5时的1维stackblur的计算方法，此时是计算Pixel 3的值。

此时Sum(Stack) = 1 + 2 * 2 + 3 * 3 + 4 * 2 + 5 = 27。

然后，算出Pixel3 = Sum(Stack)/9 = 3 。

计算Pixel 3时状态

接着更新Stack、StackOut和StackIn。

接下来我们计算Pixel 4的值。

接下来计算Pixel 4的值：

此时Sum(Stack) = 2 * 1 + 3 * 2 + 4 * 3 + 5 * 2 + 6 * 1 = 36

然后，算出Pixel 4 = Sum(Stack)/9 = 4。

接着更新。。。

计算Pixel 4时的状态

从Pixel 3和4的计算方式，我们可以得知，Sum(Stack)/9其实等价于滤波核为[1, 2, 3, 2, 1] * 1/9的1维滤波计算。

同理可知，在StackBlur的kernel size为3时，对应的1维kernel 为 [1, 2, 1] * 1/4，扩展到2维之后，见下图：

kernel size为3x3的StackBlur滤波核

再进一步，我们知道boxBlur和stackBlur类似，boxBlur应该可以用Stack、StackOut和StackIn这种模式计算，确实，我们只需要将上面两个图简化一下就是boxBlur的模式。

将Stack、StackOut和StackIn改写成Box、BoxOut和BoxIn，将Stack改成Box的格式，计算pixel 3时如下图：

boxBlur计算pixel 3时状态

这里的Box、BoxOut和BoxIn的更新方式和上面如出一辙，这里就不再赘述，下面是计算pixel 4时的状态：

boxBlur计算pixel 4时状态

而高斯模糊是无法改写成这种模式的。

到此，我们可以回答之前埋下的坑：高斯模糊的耗时会随着kernel size的增大而增大，对于StackBlur和BoxBlur，其并不会随着kernel size增大而耗时增加。这是为什么？

举个例子，对比1维滤波核的kernel size = 3和kernel size=101时所需要的计算量，对比Stack、StackOut和StackIn这种模式和普通滤波计算需要消耗的计算量：

Stack、StackOut和StackIn这种模式：每算出一个像素点值都需要更新Stack、StackOut和StackIn外加一个除法，这个计算量不会随着kernel size增加而增加。

而高斯滤波计算只能按照普通滤波计算：kernel size =3 时，需要2次加法、2次乘法和1次除法，而kernel size=101时，则需要101次加法、101次乘法和1次除法。

普通滤波计算：滤波核为[a, b, c] * 1/d时
val[i] = (input[i] * a + input[i+1] * b + input[i+2] * c)/d

---

Stackblur：加速优化

对于2维图像上的Stackblur算法，可以将其看成：先在水平方向进行1维stackblur算法；然后，在垂直方向进行1维stackblur算法。由于两个方向的优化技巧不一样，接下来的Stackblur优化也分为两部分。除此之外，还有一些其他有效的trick，经过一系列优化，stackBlur甚至比boxBlur还快。

优化水平方向的Stackblur

多线程并行加速：水平方向上计算时，每行都不相关，可以在行方向上并行加速，不多赘述。

在之前的StackBlur算法介绍部分我们知道，StackBlur算法中，有三个东西需要维护，Stack、StackIn和StackOut。其实严谨一点的表示是这样的：用Sum_Stack表示Sum(Stack)求和之后的值，Sum_StackIn和Sum_StackOut同理。更新流程变成下面过程：

Step0: 初始状态。计算初始的Sum_StackOut、Sum_StackIn和Sum_Stack。
Step1: 计算输出像素值。val = Sum_Stack/Stack_NUM.
Step2: 更新Sum_StackOut、Sum_StackIn和Sum_Stack，更新方法如下：
       Sum_Stack = Sum_Stack - Sum_StackOut + Sum_StackIn；
       StackIn和StackOut向右移动一格，类似于滑动窗口：
       Sum_StackOut = Sum_StackOut + pixel_in0 - pixel_out0
       Sum_StackIn = Sum_StackIn + pixel_in1 - pixel_out1
Step3: 重复Step1，直到一行结束。

其中，pixel_in0, pixel_out0, pixel_in1, pixel_out1是StackOut和StackIn滑动窗口移除和增加的像素值。

此类算法加速思路有一下三点：

• 优化内存
• 减少计算量
• 尝试用SIMD指令加速

对于第一点，每一行的内存都是连续的，没有优化空间。对于第二点，算法比较简单，也没法减少计算量。可以尝试的只有第三点：SIMD指令加速。仔细观察一下式：

Sum_Stack = Sum_Stack - Sum_StackOut + Sum_StackIn

乍一看，好像没法用SIMD加速，因为只有算出第N个像素，才能算出第N+1个像素，前后相关性强。

仔细观察Diffs = - Sum_StackOut + Sum_StackIn 部分，如下图：

StackOut和StackIn的diff分析

对于上图，我们可以尝试将Diffs 改写成下列式子：

Diffs = -(1 + 2 + 3) + (4 + 5 + 6)
      = (4 - 1) + (5 - 2) + (6 - 3)
      = diff0 + diff1 + diff2
其中，diff0 = (4 - 1), diff1 = (5 - 2), diff2 =  (6 - 3)

我们可以算出所有像素点之间的diff0~diffN的差值， 并保存在一个diff_vector里。其中计算前后差值(diff0和diff1)之间不是前后相关，这个过程就可以用SIMD指令加速了。这里的diff_vector的大小和输入数据一样宽，也算是空间换时间的算法。

优化之后的算法可以表示成：

Step0: 计算diff值保存到diff_vector中。
Step1: 初始状态。计算Sum_StackOut、Sum_StackIn、Sum_Stack和Diffs。
       其中Diffs = - Sum_StackOut + Sum_StackIn
Step1: 计算输出像素值。val = Sum_Stack/Stack_NUM.
Step2: 更新Diffs和Sum_Stack，更新方法如下：
       Sum_Stack = Sum_Stack + Diffs
       Diffs = Diffs - diff_vector[i] + diff_vector[j]
Step3: 重复Step1，直到一行结束。

在实际测试中，此trick能提速30%左右。

此方法参考自：https://www.cnblogs.com/imageshop/p/5053013.html

将普通滤波计算划分成StackOut、StackIn和Stack这种模式，并不全都会获得加速。想象一下，当kernel size为3时，也就是滤波为[1, 2, 1] * 1/4时，我们可以按照下普通方式计算出每个像素的值：

val = (input[i] + input[i+1] * 2 + input[i+2])/4

并且，此时前后像素的输出是完全无关，也就是所有计算都可以用SIMD指令。

实际测试发现，在水平计算上，仅当(kernel size <= 9)我们按照普通滤波计算，而kernel size > 9的情况，就按照上述的StackOut、StackIn和Stack这种模式计算。9这个数字是我在M1芯片上实际测试对比的结果。

优化垂直方向的Stackblur

多线程策略：垂直方向计算时，不同列的数据是不相关。并行方案如下图所示：

垂直方向计算的多线程策略

除并行之外，相比于水平计算时，垂直计算的最大问题时内存的不连续。滑动窗口在垂直方向移动，上一个像素点和下一个像素点在内存上是跳跃的，跳跃间隔为图像宽度。如果按照一列一列的计算，将会有巨大的I/O开销，对此，采取空间换时间的策略是非常很有效的，具体策略如下：

Sum_Stack不在是一个标量，而是一个vector，vector的长度和为图像的宽度（如果有并行，则为当前thread处理部分的宽度。）同样，Sum_StackOut和Sum_StackIn以及Queue都需要类似的处理，每次滑动都可以算出一行。此处行与行之间不相关，可以放心使用SIMD指令加速。在垂直方向优化中，不需要其他多余的trick，就能让算法跑的飞快。实际测试中，在采取空间换时间的前后，速度差距有几十倍。

StackBlur的计算优化

StackBlur是一种高斯模糊的近似计算，鉴于除法运算是比较耗时的，我们可以近似运算替代。对于数据格式为float，我们可以用乘法代替除法。对于数据格式为int型（OpenCV常用uchar型）可以用乘法和右移运算代替。

如：1/9 可以用 (v * 456) >> 12 替代。100 / 9 = 11.11, (100 * 456)>>12 = 11。

实际实现中，可以提前算出radius为0～254的乘法和右移因子，如下所示：

static unsigned short const stackblurMul[255] =
        {
                512,512,456,512,328,456,335,512,405,328,271,456,388,335,292,512,
                454,405,364,328,298,271,496,456,420,388,360,335,312,292,273,512,
                482,454,428,405,383,364,345,328,312,298,284,271,259,496,475,456,
                437,420,404,388,374,360,347,335,323,312,302,292,282,273,265,512,
                497,482,468,454,441,428,417,405,394,383,373,364,354,345,337,328,
                320,312,305,298,291,284,278,271,265,259,507,496,485,475,465,456,
                446,437,428,420,412,404,396,388,381,374,367,360,354,347,341,335,
                329,323,318,312,307,302,297,292,287,282,278,273,269,265,261,512,
                505,497,489,482,475,468,461,454,447,441,435,428,422,417,411,405,
                399,394,389,383,378,373,368,364,359,354,350,345,341,337,332,328,
                324,320,316,312,309,305,301,298,294,291,287,284,281,278,274,271,
                268,265,262,259,257,507,501,496,491,485,480,475,470,465,460,456,
                451,446,442,437,433,428,424,420,416,412,408,404,400,396,392,388,
                385,381,377,374,370,367,363,360,357,354,350,347,344,341,338,335,
                332,329,326,323,320,318,315,312,310,307,304,302,299,297,294,292,
                289,287,285,282,280,278,275,273,271,269,267,265,263,261,259
        };

static unsigned char const stackblurShr[255] =
        {
                9, 11, 12, 13, 13, 14, 14, 15, 15, 15, 15, 16, 16, 16, 16, 17,
                17, 17, 17, 17, 17, 17, 18, 18, 18, 18, 18, 18, 18, 18, 18, 19,
                19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 20, 20, 20,
                20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 21,
                21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21,
                21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 22, 22, 22, 22, 22, 22,
                22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22,
                22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 23,
                23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23,
                23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23,
                23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23,
                23, 23, 23, 23, 23, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24,
                24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24,
                24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24,
                24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24,
                24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24
        };

在我本机M1芯片上，此trick并未有非常明显的速度提升。可能原因：现在的芯片都有FPU单元，float乘法计算会很快。

性能测试：stackBlur vs GaussainBlur vs boxBlur

上面做了这么多trick和优化，实际表现究竟怎么样呢？请看下面实验。

测试环境：Mac M1，8核，image size [1920 x 2048], 数据类型：CV_8U3C。

测试方法：跑一千次，选取最小作为耗时，测试脚本在这里，欢迎大家自行测试，不同设备结果会些许差异。

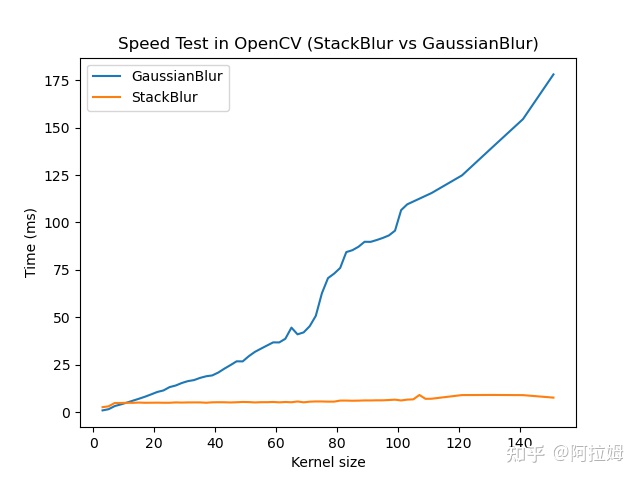
不同kernel size下高斯模糊和StackBlur的耗时对比

图像除了要考虑到数据类型int和float，还要考虑通道数，目前OpenCV常用的通道数为1，3，